Die Wälzkontaktermüdung ist eine bei Wälzlagern und vergleichbar belasteten Maschinenelementen typische Ausfallart. Die grundlegende Forschungsarbeit auf diesem Gebiet haben Lundberg und Palmgren geleistet [1] [2]: Die Lundberg-Palmgren-Theorie beschäftigt sich insbesondere mit Ermüdungsvorgängen unterhalb der Oberfläche von Wälzkontakten und basiert auf Berechnungen der idealen Hertz’schen Spannung. Dagegen betrifft die Oberflächenermüdung von Wälzkontakten („Surface Rolling Contact Fatigue“, SRCF) den oberflächennahen Bereich (bis zu einer Tiefe von nur wenigen Mikrometern). Der wiederum wird stark beeinflusst durch lokal wirkende Beanspruchungen und Spannungen infolge von geometrischen Oberflächeneigenschaften wie Rauheit, Profilabweichungen, Eindrückungen usw. Dabei ist es wichtig, die Wechselwirkungen zwischen dem elastohydrodynamischen Schmierfilm und den tatsächlich, an der Oberfläche spannungserhöhend wirkenden Faktoren zu kennen, um das Phänomen der Oberflächenermüdung bei Wälzlagern besser verstehen zu können (Morales-Espejel/Gabelli [3]). In diesem Artikel wird der SRCF-Schadensfortschritt untersucht, indem der Kontakt und die Wechselwirkungen der Oberflächenmikrogeometrie modelliert werden. Ein Vergleich der numerischen Simulationen mit verschiedenen Versuchsergebnissen deutet auf eine gute Übereinstimmung hin und ermöglicht so die Formulierung einer Hypothese über die zugrundeliegenden Mechanismen der SRCF, ihre Entstehung und ihren Schadensfortschritt bei Wälzlagern. Die neuen Erkenntnisse passen sehr gut in das Grundkonzept des „SKF Generalized Bearing Life Model“ (GBLM), das zwischen Ermüdungsschäden an der Oberfläche und denen unterhalb der Oberfläche unterscheidet [4][5].

Theoretische Untersuchungen des Schadensfortschritts
Die im Wälzkontakt aufgrund der Oberflächenmikrogeometrie entstehenden Ermüdungsschäden führen oft zu Ausbrüchen, deren Ausbreitung in ihrer fortgeschrittenen Form stark von der Makrogeometrie eines Wälzkontakts beeinflusst wird – hier insbesondere die Laufbahnkontaktgeometrie in einem Wälzlager und dem hieraus resultierenden Gesamtspannungsfeld. Verschiedene Wissenschaftler haben die Ausbreitung von Ausbrüchen in Wälzlagern untersucht, um die den Schadensfortschritt vorantreibenden mechanischen Aspekte damit in Verbindung zu bringen.

In einer von den Autoren des vorliegenden Artikels kürzlich durchgeführten Untersuchung [6] wurde der SRCF-Fortschritt anhand eines Modells und mittels Versuchen bei Wälzlagern überprüft, deren Laufbahnen zuvor mit Eindrücken versehen worden waren. Hierbei ergab sich, dass zum Verständnis der typischen V-förmigen Risse entlang der Laufbahn bei Kugellagern die Schmierbedingungen und die Wechselwirkung der Spannungen zwischen dem an und unterhalb der Oberfläche liegenden Bereich berücksichtigt werden müssen. Diese Risse unterscheiden sich vom anfänglich quer verlaufenden Schadenswachstum bei Rollenlagern, was sich dort durch die nicht geschmierten Kontakte ausreichend erklären lässt.

Experimentelle Untersuchungen des Schadensfortschritts
Snare [7] hat in seiner statistischen Analyse der Lagerzuverlässigkeit die Ausbreitung eines Ausbruchs in einem Zylinderrollenlager beobachtet und aufgezeigt, wie der Schaden sich deutlich quer zur Laufbahn hin ausbreitet, bevor er sich entlang der Laufbahn weiter fortpflanzt. Bild 1 zeigt die experimentellen Tests von Snare.

Derzeitiger Wissensstand
Ausgehend von den in der Literatur vorhandenen theoretischen und experimentellen Untersuchungen lassen sich bei Oberflächenschäden mindestens zwei unterschiedliche Ausbreitungsphasen von Ausbrüchen deutlich unterscheiden. Die erste Phase beinhaltet die mehr oder weniger langsame Ausbreitung des Ausbruchs quer zur Laufbahn; in der zweiten Phase pflanzt sich der Ausbruch schneller entlang der Laufbahn fort. Man nimmt an, dass die Gründe für den sich anfangs quer zur Laufbahn hin ausbreitenden Ausbruch darin zu finden sind, dass an den sich diametral gegenüberliegenden Rändern des Ausbruchs (also orthogonal zur Laufrichtung) höhere Spannungen vorliegen als im vorderen und hinteren Bereich des Ausbruchs.

Bei Kugellagern (Bild 2) und Rollenlagern (Bild 3) zeigt sich ein ganz unterschiedliches Verhalten bei der Entstehung und Ausbreitung von Ausbrüchen. Die an der Oberfläche von Kugellagern entstehenden Ausbrüche bilden sich anfangs in charakteristischer V-Form im hinteren Bereich der Eindrückung und pflanzen sich schnell in Laufrichtung fort, während sich aus dem V-förmigen Bereich Laufbahnmaterial ablöst. Der Ausbruch breitet sich dann in Laufrichtung aus – also entgegengesetzt zu der an dieser Stelle vorhandenen Reib- und Gleitrichtung (Bild 2). Die von der Oberfläche bei Rollenlagern ausgehenden Ausbrüche pflanzen sich anfangs von beiden Seiten des Ausgangspunkts fort und wachsen quer zur Laufbahn, bevor sie sich entlang der Laufbahn ausbreiten (Bild 3).

Ziel dieses Artikels ist es, den derzeitigen Wissenstand zum Schadensverlauf von Rollenlager-Ermüdungsschäden darzustellen, welche von der Oberfläche ausgehend das Lager schädigen. Aufgabe ist es, durch eine Vielzahl von Modellierungen und durchgeführten Versuchen den treibenden Mechanismus, der für den Schadensfortschritt verantwortlich ist und von den Autoren in der Arbeit [3] beschrieben wurde, darzustellen.

Experimentelle Arbeit
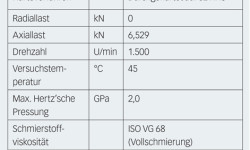
Die Versuche wurden an Standardkegelrollenlagern durchgeführt (siehe Tabelle 1).

Die Kegelrollenlager wurden mit künstlich erzeugten Eindrückungen versehen, indem ihnen mittels eines Wolframkarbid-Kugeleindringkörpers mit einem Durchmesser von 1 mm eine Eindringkraft von 1.250 N auferlegt wurde. Unter dieser Belastung entstanden Eindrückungen mit einem Durchmesser von 400 µm, einer Tiefe von 30 µm und einem erhöhten Rand von rund 2 µm. Der Versuch wurde an acht, im gleichen Abstand voneinander am Umfang der Kegelrollenlagerinnenringe angeordneten Eindrucksstellen durchgeführt. Die Eindrückungen wurden auch in Abständen von 0,5 mm ab Laufbahnkante quer über die Laufbahn angeordnet. In diesem Artikel wird allerdings nur der Schadensfortschritt bei den Eindrückungen in der Laufbahnmitte detailliert behandelt. Unter den in Tabelle 1 genannten Betriebsbedingungen führte die Axialbelastung zu einer Hertz’schen Kontaktbreite in Laufrichtung von rund 142 µm, die erheblich kleiner ist als der Durchmesser der Eindrückung. Die Versuche wurden mit unterschiedlichen Umdrehungszahlen durchgeführt, um den aus den Spannungskonzentrationen und Schmierbedingungen an den Eindrückungen resultierenden Fortschritt des Ermüdungsschadens beobachten zu können.

Bild 4 zeigt ein paar Versuchsergebnisse über die Ausbreitung einer Eindrückung mit Ausbrüchen in einem Kegelrollenlager bei einer zunehmenden Anzahl von Umdrehungen. Die auf einer Seite der Eindrückung entstandenen Ausbrüche pflanzten sich an beiden Seiten der Eindrückung quer zur Laufbahn (also orthogonal zur Laufrichtung) fort. In Bild 4(b) wurde eine angenäherte Kontaktellipse eingezeichnet, um einen Vergleich mit den endgültigen Ausbrüchen zu ermöglichen. Einige Innenringe wurden mit dem Mikroskop im Abstand von 5 Mio. Umdrehungen periodisch überprüft, um den Beginn und die Ausbreitung der Ausbrüche festzustellen. Jede Eindrückung wurde dabei mikroskopisch untersucht und fotografiert. Die Entstehung und Ausbreitung des Bereichs mit Ausbrüchen um die Eindrückung herum wurden mittels digitaler Bildverarbeitung der gesammelten Mikrofotos der verschiedenen Eindrückungen ausgemessen. Die Ergebnisse dieser detaillierten Untersuchung lieferten in Abhängigkeit von der Anzahl der Umdrehungen sehr genaue Angaben über das anfängliche und fortschreitende Schadenswachstum des mit Ausbrüchen versehenen Bereichs. Sämtliche Daten, die bei den sechs einzelnen Eindrückungen gesammelt wurden, an denen sich Ausbrüche zeigten, sind in Bild 5 dargestellt.

Eine genauere Untersuchung der durchschnittlichen Versuchsdaten weist darauf hin, dass die Ausbreitung des Bereichs mit Ausbrüchen einem dreistufigen Prozess unterliegt:

1. Die „Inkubationszeit“ mit 50
bis 60 Mio. Umdrehungen, in der kein sichtbarer Schaden an der Lagerlaufbahn feststellbar ist.
Sie entspricht in etwa der Ermüdungslebensdauer des Lagers.
2. Die Phase des beginnenden Schadensfortschritts mit 30 bis 40 Mio. Umdrehungen: Wie erwartet, zeigt sich im geschädigten Bereich ein exponentielles Schadenswachstum.
3. Die Phase des beschleunigten Schadenswachstums mit 20 bis 25 Mio. Umdrehungen. In dieser Phase nimmt die Schadenswachstumsrate erheblich zu (um mehr als das Doppelte im Vergleich zur vorherigen Phase).

Schadensfortschritts­modell
Bei der Berechnung des Schadens im Wälzkontakt wird zunächst einmal die anfängliche Eindrückung der Laufbahn modelliert. Dabei bedient man sich einer parametrischen, analytischen Funktion, die die Form der tatsächlichen Eindrückung genau nachbildet.

Die Geometrie des Eindrucks wird dann in ein Überrollkontaktmodell übernommen, um die zyklische Hertz’sche Spannung des jeweiligen Prüflagers nachzubilden. Die Berechnung des Schadensfortschritts erfolgt nun anhand des von Morales-Espejel und Brizmer zuvor bereits entwickelten, grundlegenden Oberflächenermüdungs- und Ablösungsmodells [8]. Dieses Modell wird in der angegebenen Literatur umfassend beschrieben. Allerdings wurden auch einige Änderungen und Anpassungen vorgenommen. Beispielsweise wurde die in [8] beschriebene Verschleißberechnungsroutine ausgeschaltet, um die numerischen Simulationen zu beschleunigen. Das schnelle Berechnungsmodul für die Schmierung ist ebenfalls ausgeschaltet, und es wird nur das Modell für nicht geschmierte Kontakte für Situationen verwendet, in denen die anfängliche Eindrückung breiter ist als der Hertz’sche Kontakt in Laufrichtung (wie beim simulierten Kegelrollenlager in Bild 4 (a)). Das Modell wird dann zur Berechnung der Gesamtdruckverteilung und Gesamtspannungen verwendet. Diese Näherung ist gültig, da der Schmierstoff in diesem Fall wahrscheinlich aus der Eindrückung und dem Kontakt verschwindet. Es ist nicht damit zu rechnen, dass sich im Randbereich der Eindrückung hydrodynamischer Druck aufbaut, so dass die Drücke dort also mit der Hypothese für nicht geschmierte Kontakte modelliert werden können. Bei Kugellagern mit einem breiteren Hertz’schen Kontaktbereich kann das Schmiermodell nicht ignoriert werden.

Sobald die Kontaktdrücke berechnet sind, ergibt sich die Spannungshistorie für eine Reihe von Zeitschritten, die simulieren sollen, wie die Eindrückung den Wälzkontakt durchläuft (siehe [5]).  Aus diesem mehrstufigen Simulationsprozess heraus kann die Ermüdungsspannungshistorie zur weiteren Verarbeitung berechnet werden. Hierbei bedient man sich des Ermüdungskriteriums, um den Ermüdungsschaden einschätzen zu können, der sich seit Beginn bis zum aktuellen Lastzyklus kumuliert hat. Dieses Schema entspricht genau der gleichen Datenverarbeitung, die Morales-Espejel und Brizmer [8] eingeführt haben. Der bis zum aktuellen Lastzyklus kumulierte Gesamtschaden wird mit der Palmgren-Miner-Regel berechnet.

Wenn die Ermüdung einen kritischen Schadenswert erreicht, kann es zu Rissbildung innerhalb des Werkstoffs kommen. Das aktuelle Schema sieht aber kein detailliertes Risswachstumsmodell vor; der Schadensfortschritt wird simuliert, indem das ermüdete Material schlicht entfernt wird. Zu diesem Zweck wurde ein einfaches Materialablösungsmodell [8] implementiert, dessen Aufgabe die Beseitigung des angefallenen, kritisch geschädigten Materials und des darüber liegenden Materials ist. Dieses Modell sieht auch einen Tiefenschwellenwert (h) für die darunter liegende Oberfläche vor, deren kritisch geschädigtes Material nicht entfernt werden darf. Dieser Tiefenschwellenwert kann von h = 0 bis h = ∞ eingestellt werden. Die Einstellung h ≥ 0 ermöglicht eine Ablösung des Materials unterhalb der Oberfläche. Das aktuelle Modell kann keine genaue Angabe zum Schadenswachstum machen, wenn der Parameter „h“ nicht im Voraus bekannt ist oder verschiedene Versuchsergebnisse nicht verfügbar sind. Aber es kann die Schadenswachstumsbereiche sehr gut beschreiben; dies wird nachfolgend näher ausgeführt. Der Berechnungsprozess wird für eine vorgegebene Anzahl von Lastzyklen wiederholt (bis zu einer Höchstzahl von üblicherweise > 10⁹ Überrollungen), und danach wird die Schadensfortschrittshistorie ausgewiesen.

Modellergebnisse
In Tabelle 1 sind die Versuchsdaten aufgeführt. In diesem Fall sind die Eindrückungen breiter (Durchmesser 400 µm) als der Hertz’sche Kontakt in Laufrichtung (142 µm); so kann sich beim Überrollen die erforderliche EHD-Druckverteilung über der Eindrückung nicht aufbauen. Dies führt zum Zusammenbruch des Ölfilms am Rand des mit Eindrückungen versehenen Bereichs. Unter diesen Bedingungen kann der Einfluss des Schmierfilms aus der Analyse ausgeschlossen werden, und der Schadensfortschritt kann einfach mithilfe der Näherung für nicht geschmierte Kontakte simuliert werden.

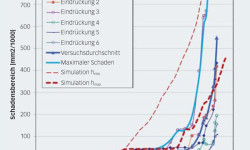
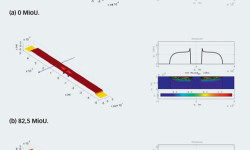
Bild 6 zeigt die Entwicklung der Ausbrüche ausgehend von der anfänglichen Eindrückung bei einer zunehmenden Anzahl von Umdrehungen; es werden auch die fortschreitenden Änderungen der Hertz’schen Pressung und die damit zusammenhängenden Spannungen unterhalb der Oberfläche gezeigt. Die Ergebnisse der numerischen Simulationen lassen die bevorzugte Richtung deutlich erkennen, in der sich der Bereich mit Ausbrüchen entwickelt. Der Schaden beginnt an den Seitenrändern der Eindrückung und setzt sich axial quer zur Laufbahn in ähnlicher Weise fort, wie in den Versuchen beobachtet (siehe Bild 4). Durch Berechnung des geschädigten Bereichs erhält man die Kurve „Schadensfortschritt vs. Anzahl der Lagerumdrehungen“. Diese wurde mit zwei Tiefenschwellenwerten h gerechnet, das heißt, einem Mindest- und einem Höchstwert, um den Umfang der Modellsimulationen zu kennzeichnen (h_min berührt gerade einmal den Bereich der maximalen orthogonalen Schubspannung um die Eindrückung herum, während h_max darüber hinausgeht). Die hieraus resultierenden Schadensfortschrittskurven sind mit gestrichelten Linien in Bild 5 dargestellt. Eine dünne gestrichelte Linie ist das Ergebnis der konservativsten Einstellung bei der Einschätzung der von der Oberfläche ausgehenden Mikroausbrüche – das heißt, sie entspricht dem minimalen Tiefenschwellenwert. Daher stellen die simulierten Ergebnisse eine sichere Schadensgrenze dar und definieren die Bedingungen für den maximal zu erwartenden Schadensbereich sämtlicher von der Oberfläche ausgehender Ausbrüche.

Nach Einführung des maximalen Tiefenschwellenwerts h zeigt die Entwicklung des in Bild 5 mit einer dick gestrichelten Linie gekennzeichneten Schadens eine realistischere Übereinstimmung mit den Versuchsergebnissen. Deutlich erkennbar ist der anfängliche Trend des berechneten Schadens­bereichs, der eine ­schrittweise Fortentwicklung zeigt, die sich genau mit einigen experimentellen Messungen deckt. Dieser Trend erreicht zwischen 90 und 120 Mio. Umdrehungen eine stabile Wachstumsrate; dieses Intervall kann mit der gemessenen anfänglichen Fortschrittsphase des Schadenswachstums der Eindrückung verglichen werden, die im Abschnitt „Experimentelle Arbeit“ beschrieben wird.

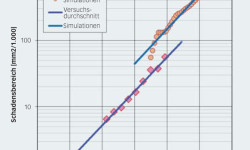
Bild 7 zeigt die Schadenswachstumsrate der Versuche im Vergleich zu der bei den numerischen Simulationen erreichten Schadenswachstumsrate, die bei 11,5 Mio. Umdrehungen liegt (134 Mio. Zyklen). Diese gute Übereinstimmung zwischen dem Durchschnitt der Versuchsergebnisse und den numerischen Simulationen zeigt, dass die Berechnung in der Lage ist, einige Haupteinflüsse der Mechanismen der Oberflächenermüdung und der beginnenden Schälung zu erfassen. Darüber hinaus weisen die Versuchsergebnisse auf ein beschleunigtes Wachstum nach 100 Mio. Umdrehungen hin. Allerdings scheint das aus den Ergebnissen der numerischen Simulationen überhaupt nicht hervorzugehen. Eine mögliche Erklärung für dieses Verhalten könnte sein, dass die Bildung eines Bereichs mit Ausbrüchen auch zusätzliche Belastungen aufgrund der dynamischen Reaktion des Lagers auf die Ausbrüche entstehen lässt. Diese zusätzlichen Belastungen sind momentan im Modell nicht enthalten; daher kann lediglich der anfängliche Schaden durch Ausbrüche mit den numerischen Simulationen einigermaßen verglichen werden.

Bei den simulierten Ergebnissen ist auch der Mechanismus des Schadensfortschritts von Interesse. Weil die Eindrückung etwas größer ist als die Hertz’sche Breite in Laufrichtung, stellt der seitliche Bereich der Eindrückung die am stärksten belastete Zone der Laufbahn dar, wo der Schaden tatsächlich beginnt und sich weiterentwickelt. Dieser Schadensfortschrittsmechanismus lässt sich auch in der numerischen Simulation finden: Hier ist der Seitenrand des Ausbruchs von den höchsten Flächenpressungen und unter der Oberfläche liegenden Spannungskonzentrationen betroffen (Bild 6). Diese Art der Ausbreitung von Ausbrüchen scheint typisch für Rollenlager zu sein.

Schlussfolgerungen
Es wurden Versuche an Kegelrollenlagern durchgeführt, deren Laufbahnen mit vorgegebenen Eindrückungen versehen worden waren. Die verschiedenen dabei entstandenen Spannungsüberhöhungen führten zu Ausbrüchen an den Laufbahnoberflächen, welche eine detaillierte Untersuchung ihrer Bildung und fortschreitenden Entwicklung ermöglichten. Ein vorhandenes Modell für die Oberflächenermüdung von Mikrogeometrien (Morales-Espejel/Brizmer [8]; das heißt, für die Oberflächenzerrüttung) wurde angepasst, um den von der Oberfläche ausgehenden Prozess der Bildung von Makroausbrüchen untersuchen zu können.

Das Modell wurde angewendet, um ein besseres Verständnis von der frühen Phase der Bildung und Ausbreitung von Ausbrüchen zu erhalten. Aufgrund der Berechnungsergebnisse lässt sich sagen, dass das numerische Modell tatsächlich viele der experimentellen Beobachtungen simulieren und erklären kann; insbesondere die Versuchsergebnisse ließen darauf schließen, dass sich bei den Kegelrollenlagern die Ausbrüche anfänglich quer zur Laufbahn, also orthogonal zur Laufrichtung, ausbreiten. Bei Lagern mit Linienberührung ist es im Allgemeinen so, dass die Spannungen in den seitlichen Bereichen einer Eindrückung höher sind. In der anfänglichen Ausbreitungsphase der Ausbrüche beschleunigen diese höheren Spannungen das Wachstum der Ausbrüche quer zur Laufbahn hin.

Aus den Ergebnissen der bisherigen Arbeit können folgende Schlüsse gezogen werden:

1. Bei Rollenlagern mit zuvor angebrachten Eindrückungen wachsen die Ausbrüche anfangs quer zur Laufbahn; diese Entwicklung ist bedingt durch die höheren Spannungen, die an den Ausbruchs­rändern orthogonal zur Laufrichtung vorhanden sind. Dies wurde bereits in der Fachliteratur behandelt.
2. Das vorgestellte Modell kann die beiden Schadensfortschrittsmechanismen gut beschreiben. Insbesondere bei Rollenlagern zeigt die Wachstumsrate der beginnenden Ausbrüche eine deutliche Korrelation zwischen den Simulationsergebnissen und den experimentellen Messungen.

Danksagung
Dieses Projekt wurde teilweise von der EU-Kommission im Rahmen einer Marie-Skłodowska-Curie-Maßnahme (Industry-Academia Partnerships and Pathways, IAPP) als Forschungsprojekt iBETTER finanziert.

http://cordis.europa.eu/project/rcn/109976_en.html

Literatur
[1] Lundberg, G. and Palmgren, A. (1947), “Dynamic Capacity of Rolling Bearings,” Acta Polytechnica, 1(3), pp 1–52.
[2] Lundberg, G. and Palmgren, A. (1952), “Dynamic Capacity of Roller Bearings,” Acta Polytechnica, 2(4), pp 96–127.
[3] Morales-Espejel, G. E. and Gabelli, A. (2011), “The Behavior of Indentation Marks in Rolling Sliding Elastohydrodynamically Lubricated Contacts,” Tribology Transactions, 54, pp 589–606.
[4] Morales-Espejel, G.E., Gabelli, A. de Vries A. (2015), “A Model for Rolling Bearing Life with Surface and Subsurface Survival – Tribological Effects”, to be published at Tribology Transactions.
[5] Morales-Espejel, G.E. and Gabelli, A. (2015), “The SKF Generalized Bearing Life Model – the power of tribology,”
Evolution #4-2015, pp 22-28.
[6] Morales-Espejel, G.E. and Gabelli, A. (2015), “The Progression of Surface Rolling Contact Fatigue Damage of Rolling Bearings with Artificial Dents,” Tribology Transactions, 58, pp 418–431.
[7] Snare, B. (1970), “How Reliable Are Bearings?” The Ball Bearing Journal, 162, pp 3–7.
[8] Morales-Espejel, G. E. and Brizmer, V. (2011), “Micropitting Modelling in Rolling–Sliding Contacts: Application to Rolling Bearings,” Tribology Transactions, 54, pp 625–643.