Износ и поверхностная усталость подшипников качения
Даже в условиях тщательного наблюдения, измерения и мониторинга износ подшипников качения с трудом поддаётся прогнозированию. SKF провела всесторонние исследования и анализ особенностей скольжения и износа, а также их влияния на ресурс подшипника.
В некоторых областях применения у подшипников качения может наблюдаться значительная потеря материала (износ) вследствие недостаточного смазывания, присутствия абразивных частиц, коррозии, колебательных движений при вращении и других факторов. Такой износ, в свою очередь, может негативно сказаться на работе подшипников – от уменьшения преднатяга до необратимых последствий. Распространённым и, вероятно, неожиданным следствием неравномерного износа дорожек качения подшипников является риск более интенсивного развития поверхностной усталости. В ряде областей применения нередко можно наблюдать полосы с поверхностным разрушением или выкрашивание материала на дорожках качения. Это связано с возможным изменением профиля дорожки качения в результате неравномерного износа, что может вызвать увеличение концентрации напряжений по линиям высокого давления и линиям с недостаточной толщиной смазочной плёнки.
Работа подшипников качения при неправильном смазывании в условиях неравномерного скольжения, присутствия абразивных частиц или загрязнения жидкостями может привести к значительному изменению профилей дорожек качения (рис. 1). С течением времени такие изменения могут вызвать концентрацию напряжений в наиболее нагруженных зонах (рис. 2), что может способствовать увеличению локальной поверхностной усталости, формируя в местах повышенных напряжений на дорожке качения полосы с микротрещинами или следами выкрашивания материала (рис. 3). Такое развитие потенциальных дефектов может произойти с любым подшипником качения, однако наиболее уязвимы подшипники в узлах с сильным загрязнением, коррозией, неправильным смазыванием, неравномерным скольжением или переменными нагрузками. Подобные примеры можно найти в горнодобывающей и целлюлозно-бумажной промышленности, в ветроэнергетике и ряде других отраслей.
Износ подшипников качения – это нелинейное явление. Даже регулярный мониторинг и измерение степени износа подшипника показывают, что предположений недостаточно для того, чтобы прогнозировать характер развития износа с течением времени. Это невозможно по целому ряду причин: износ в основном зависит от локальных характеристик скольжения и нагрузки, но сам износ изменяет оба этих фактора, поэтому простая экстраполяция тут невозможна. В данном случае необходим более тщательный анализ. Именно поэтому SKF проводит исследование характеристик скольжения и износа в подшипниках качения, а также их влияния на ресурс подшипника [1].
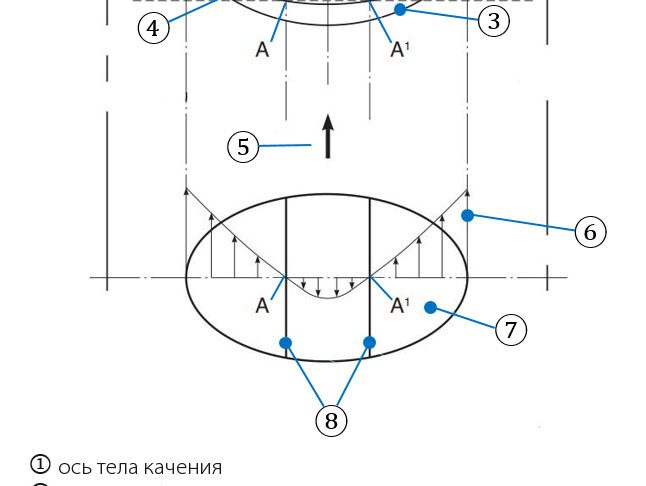
Все подшипники качения характеризуются некоторой степенью скольжения, что является нормальным явлением. Оно обусловлено внутренней геометрией подшипника и/или условиями нагружения. Например, в радиальном шарико- или роликоподшипнике, работающем в идеальных условиях радиального нагружения, также будет иметь место скольжение (Heathcote slip), определяющееся геометрией контакта тела качения / кольца и упругой деформацией от воздействия нагрузки (рис. 4a и 4b). Поскольку износ зависит от скольжения, с течением времени (при правильно заданных условиях) можно ожидать, что полосы исключительно качения (A и A1) будут единственными участками без износа. Следовательно, это будут единственные участки, на которые будет приходиться вся нагрузка в месте контакта.
К счастью, подобное может произойти только в ситуациях сильного износа, например, при наличии абразивных частиц, сильной коррозии или аномального скольжения вследствие неправильного нагружения или монтажа подшипника. В большинстве случаев подшипники работают нормально, а такое скольжение является одним из обычных эксплуатационных факторов подшипника качения, не создающих проблем.
В настоящей работе более подробно рассматриваются основные механизмы повреждения подшипников вследствие износа и усталости. Для более полного понимания этих механизмов и определения способов предотвращения негативных последствий было выполнено моделирование и проведён ряд экспериментов.
Моделирование
Моделирование износа
В работе [2] рассматриваются различные модели износа в условиях смазывания и делается вывод, что во всех случаях они могут быть представлены моделью Арчарда [3], иногда с использованием коэффициента износа, имеющего сложный алгоритм вычисления. В большинстве случаев коэффициент износа определяется эмпирически на основании результатов экспериментов. Самая общая формула износа:
где
V = объём износа [m3] за определённое время;
![]() = безразмерный коэффициент износа по Арчарду [-];
= безразмерный коэффициент износа по Арчарду [-];
F = контактное усилие [Н];
H = текущая твёрдость поверхности материала [Па];
s = расстояние скольжения [м] за определённое время.
Объём износа можно выразить следующим образом:
где
h = толщина удалённого слоя поверхности [м] за определённое время;
As = площадь скольжения [m2] за определённое время.
Таким образом, подставляя (2) в (1) и учитывая, что среднее давление контакта p ![]() :
:
Учитывая общее время контакта ![]() на цикл нагружения, которое представляет собой время прохождения обеих поверхностей скольжения через зону контакта со скоростью скольжения, площадь скольжения будет представлять собой площадь контакта, следовательно, As = A. Толщину удалённого слоя на количество перекатываний (N) можно вычислить согласно работе [2] следующим образом:
на цикл нагружения, которое представляет собой время прохождения обеих поверхностей скольжения через зону контакта со скоростью скольжения, площадь скольжения будет представлять собой площадь контакта, следовательно, As = A. Толщину удалённого слоя на количество перекатываний (N) можно вычислить согласно работе [2] следующим образом:
где
us = локальная скорость скольжения [м/с];
u1 = средняя скорость анализируемой поверхности [м/с];
l = длина контакта вдоль направления скольжения [м].
Следует отметить, что почти все значения являются локальными (x,y.) Здесь также принимается, что твёрдость стали дорожек качения и тел качения является постоянной. Формула (4) даёт локальную толщину изношенного слоя, удаляемого в месте контакта при каждом перекатывании.
Моделирование взаимного влияния износа и усталости
Для моделирования взаимного влияния износа / усталости в подшипниках модель контактной усталости при качении необходимо применить к каждому перекатыванию дорожки качения с предварительно изменённым профилем (на обеих поверхностях) вследствие износа. Именно так проявляется взаимное влияние износа и усталости. Всякий раз, когда износ приводит к изменению профиля, для усталостной модели необходим новый расчёт распределения давления в месте контакта. Такой процесс отображает то, что происходит в реальности. Однако подобный подход очень затратен в отношении вычислений, учитывая, что типичная модель контактной усталости при качении может охватывать миллионы перекатываний. Таким образом, существуют упрощения, которые значительно снижают трудоёмкость вычислений:
- Расчёт выполняется для сухого контакта, а не для условий полноценного эластогидродинамического смазывания, что в данном случае позволяет использовать (измеренный) фиксированный коэффициент трения во избежание необходимости разрешения проблемы смазывания.
- Обновление профиля вследствие износа осуществляется не через каждое перекатывание, а через их определённое число.
- Как следствие предыдущего пункта, новый расчёт контакта и усталости может производиться одновременно с новым расчётом профиля вследствие износа, а не после каждого перекатывания.
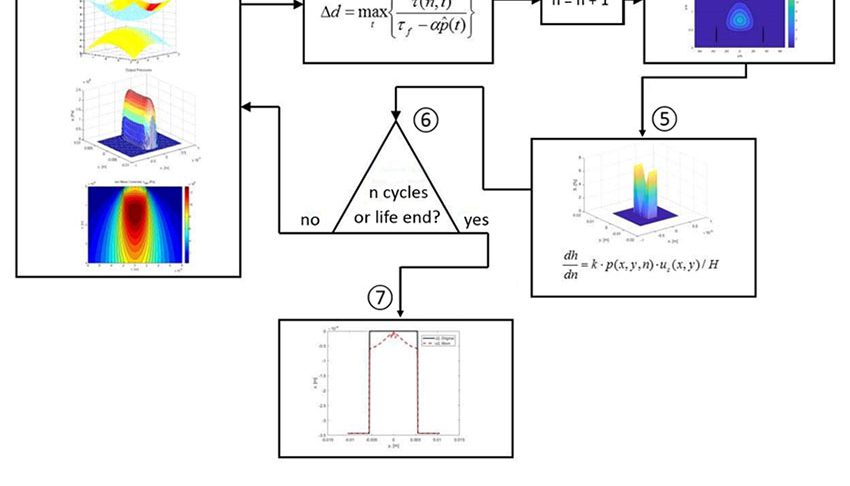
Блок-схема на рис. 5 позволяет получить обобщённое представление о методике расчёта. Следует отметить, что в данном случае используется критерий усталости Данг Вана [4], а накопление повреждений учитывается с использованием линейного закона Палмгрена-Майнера [5, 6]. Однако можно было бы использовать любой другой критерий усталости или закон накопления повреждений, если бы необходимость этого показали эксперименты.
Эксперименты
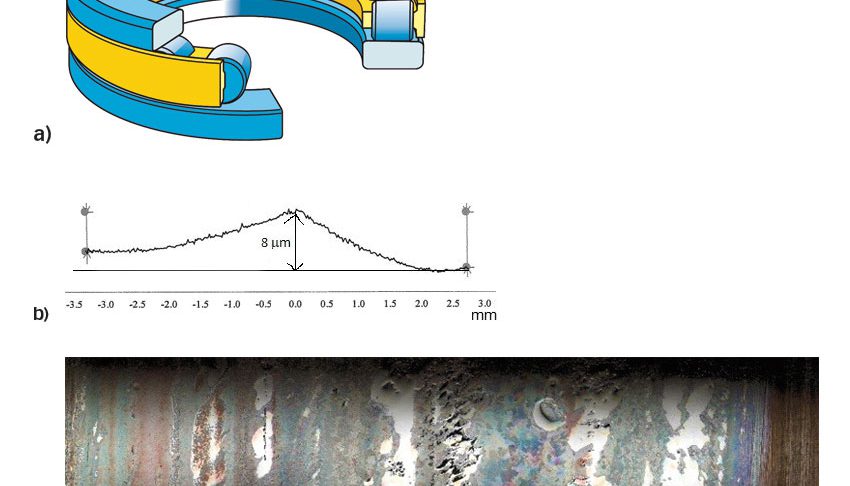
Для подтверждения модели усталости были проведены ресурсные испытания с упорным цилиндрическим роликоподшипником 81107 TN (рис. 6a) с осевым нагружением при C/P = 6,5 и условиями смазывания, соответствующими ![]() ≈ 0.5.
≈ 0.5.
Перед испытанием в новых подшипниках был искусственно создан такой профиль (рис. 6b), как если бы они работали в условиях повышенного износа. Во время испытаний некоторые подшипники вышли из строя, в основном из-за повреждения роликов (рис. 6c), чтобы модель расчёта ресурса можно было сравнить с результатами укороченных испытаний. Точно такие же изношенные ролики и новые кольца учитывались в модели, представленной на рис. 5. Результаты показали хорошую корреляцию с нижней границей срока службы L10 с учётом распределения Вейбулла.
Параллельно также проводились испытания на износ и измерения в немодифицированных подшипниках для вычисления коэффициента износа и подтверждения модели с помощью различных экспериментов. Корреляция между моделью и экспериментальными данными была также признана удовлетворительной.
Результаты
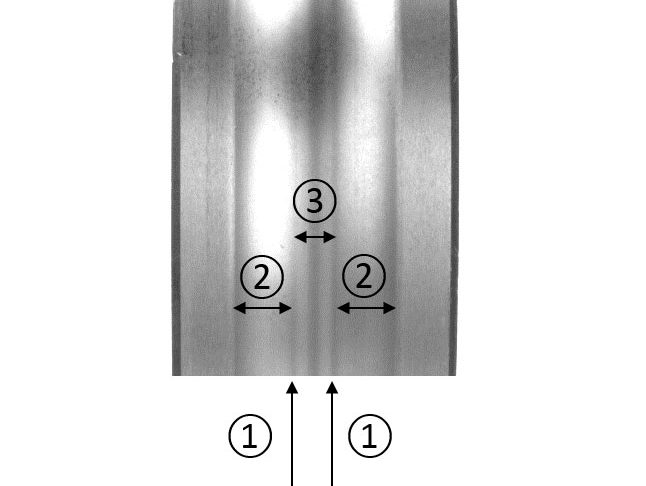
В упорных цилиндрических роликоподшипниках скольжение меняется линейно (уменьшается) от двух кромок ролика в направлении средней линии, где скольжение равно нулю (рис. 7). В направлении к наружному диаметру подшипника ролик будет иметь самую быстродвижущуюся поверхность, а к внутреннему диаметру — самую медленную. Чтобы проиллюстрировать эффект от совместного воздействия износа и усталости в подшипнике качения с переменным скольжением поперёк дорожки качения, рассматривается ситуация с упорным роликоподшипником большего размера (81212 TN) с параметрами, представленными в таблице 1.
Было проведено моделирование, при котором профиль менялся в зависимости от износа с использованием размерного коэффициента износа (определяемого как ![]() ) с условиями нагружения, указанными в таблице 1. Модель предполагала достижение 300 миллионов перекатываний.
) с условиями нагружения, указанными в таблице 1. Модель предполагала достижение 300 миллионов перекатываний.
Было определено, что в целях экономии времени вычислений вместо обновления профилей с учётом износа после каждого перекатывания такие обновления можно делать через каждые 15,5 млн перекатываний ролика без потери в точности. Для вычислений применялась модель, представленная на рис. 5, включая модель износа по Арчарду с формулой (4).
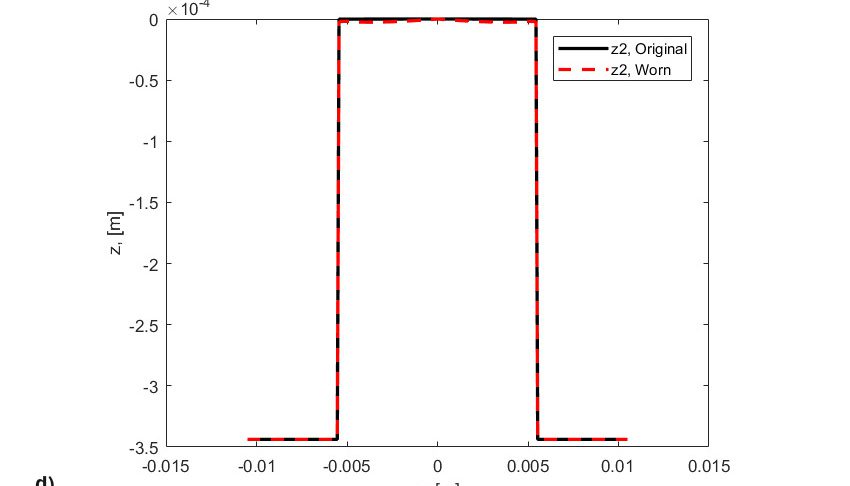
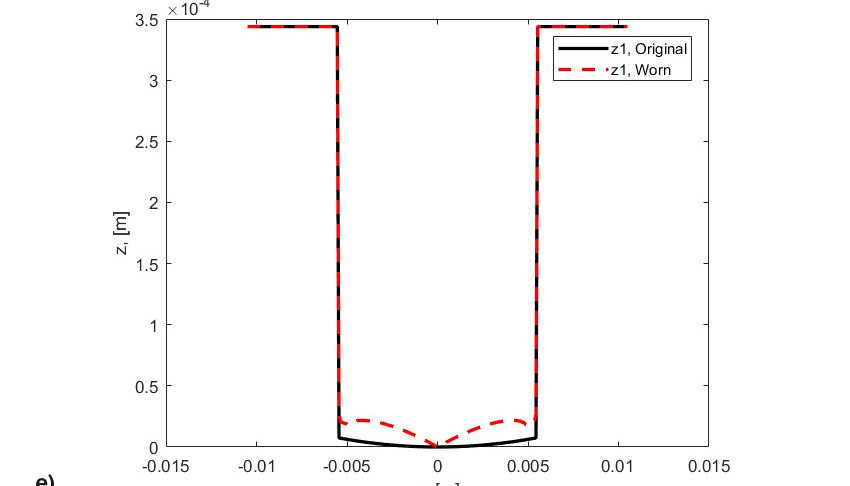
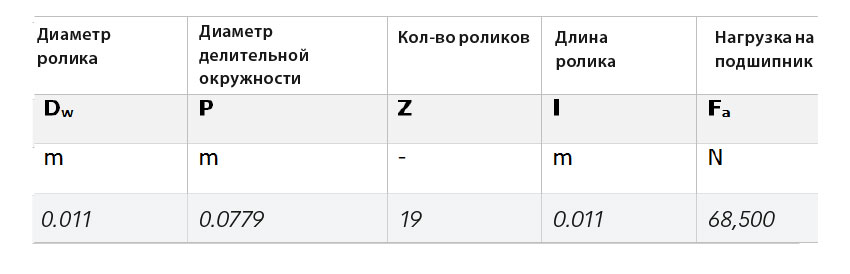
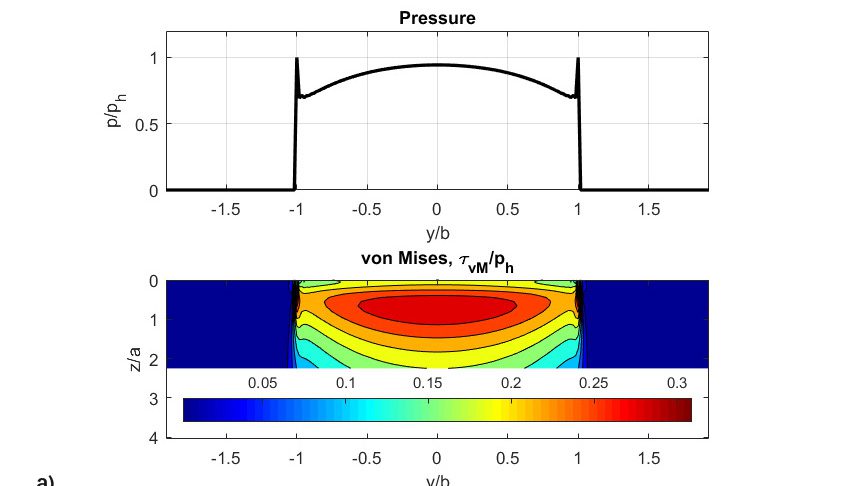
Результаты моделирования представлены на рис. 8, на котором отображены:
- безразмерное давление;
- напряжение сдвига по Мизесу;
- карта повреждений;
- исходные профили роликов и колец;
- профили изношенных роликов и колец, соответствующие завершающему этапу моделирования.
Необходимо отметить, что карта повреждений фиксирует общее значение повреждений, превышающее единицу (порог образования трещин), уже через 31 млн перекатываний. Результаты на рис. 8 относятся к начальному и заключительному этапам моделирования. Начальное давление (рис. 8а) при первом перекатывании в целом соответствует давлению по Герцу, но отражает некоторый эффект кромочных напряжений из-за использования ролика с простым прямолинейным профилем вместо профиля соответствующей формы, который позволяет избежать таких напряжений. Результаты показывают, что скольжение на средней линии равно нулю. Часть моделирования, относящаяся к модели износа по Арчарду, также показывает отсутствие износа в этой области.
Действительно, износ связан с распределением скольжения по дорожке качения. Таким образом, износ увеличивается по мере удаления от средней линии дорожки качения. Следует заметить, что сначала контактное давление действовало под почти прямым углом (рис. 8а), но по мере удаления материала с обеих сторон в месте контакта качения давление уменьшалось в зонах с высокими значениями скольжения и сильно возрастало и концентрировалось в зоне нулевого скольжения (средней линии) (рис. 8b). Такое повышенное давление создаёт большое напряжение и вызывает усталость материала с большей интенсивностью вплоть до развития повреждения в середине ролика (рис. 8c). Эффект от одновременного совместного воздействия износа и усталости может ускорить усталостное выкрашивание материала в месте контакта. Такое ускоренное выкрашивание из-за усталости не связано с фрикционным напряжением, вызванным скольжением, а является скорее результатом изменения исходного профиля тел качения (рис. 8d и 8e), приводящего к резкому увеличению контактного напряжения и локальному уменьшению толщины смазочной плёнки.
Резюме
В результате моделирования совместного воздействия абразивного износа и контактной усталости при качении выяснилось, что скольжение может стать важным фактором, способствующим развитию усталостных повреждений подшипника. Для этого в подшипнике должны присутствовать абразивные частицы и (или) неправильные условия смазывания. Неравномерное распределение скольжения в контакте Герца также способствует развитию концентраторов напряжений, которые существенно сокращают расчётный усталостный ресурс подшипника. По всем признакам это самый значимый механизм, в результате которого скольжение по Герцу может привести к уменьшению срока службы подшипника вследствие контактной усталости при качении.
Рекомендации для уменьшения подобного риска:
- Убедитесь, что обеспечивается надлежащее смазывание подшипника. Это особенно важно для крупногабаритных подшипников с низкой частотой вращения или колебаний, подшипников в условиях большого количества абразивных частиц, а также подшипников, подверженных воздействию коррозии.
- Оптимизируйте уплотнительные решения, при необходимости используйте подшипники с уплотнениями или защитными шайбами.
- Сведите к минимуму возможность загрязнения подшипника жидкостями и твёрдыми частицами.
- Избегайте ударных нагрузок и вибрации, которые могут значительно ухудшить существующие условия скольжения в подшипнике
- Если своевременно выявлен неравномерный износ крупногабаритных подшипников, следует рассмотреть возможность их восстановления, что может способствовать снижению затрат.
Авторы:
Гийермо Э. Моралес-Эспехель,
главный научный сотрудник научно-исследовательского центра SKF, Ньювегейн, Нидерланды
Автор выражает благодарность Ральфу Меуэнорду за оказанную им поддержку во время экспериментальной части проекта.
Список литературы
[1] Morales-Espejel, G.E., Gabelli, A., Rolling Bearing Seizure and Sliding Effects on Fatigue Life, Proc. IMechE, part J, Journal of Eng. Tribology, DOI: 10.1177/1350650118779174, 2018.
[2] Morales-Espejel, G.E., Brizmer, V., Piras, E., Roughness Evolution in Mixed Lubrication Condition due to Mild Wear, Proc. IMechE, part J, Journal of Eng. Tribology, 229(11), pp. 1330-1346, 2015.
[3] Archard, J.F., Contact and Rubbing of Flat Surface, Journal of Applied Physics; 24(8): 981–988, 1953.
[4] Dang Van, K., Griveau, B., and Message, O., On a New Multiaxial Fatigue Limit Criterion: Theory and Application, Biaxial and Multiaxial Fatigue, Brown, M. and Miller, K. (Eds.), Mechanical Engineering Publications: London, pp. 479-498, 1989.
[5] Palmgren, A., Die Lebensdauer von Kugellagern [Life Length of Roller Bearings], Zeitschrift des Vereines Deutscher Ingenieure (VDI Zeitschrift), 68(14), 1924,
pp 339-341. (In German)
[6] Miner, M.A., Cumulative Damage in Fatigue, Journal of Applied Mechanics, 67 A157, 1945.








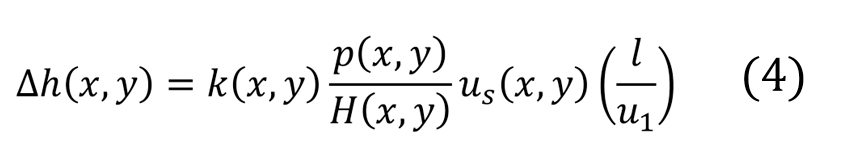

![Рис. 8: c) карта повреждений Палмгрена-Майнера после моделирования для того же примера, что и в таблице 1, с коэффициентом износа =0.5x10-11 [s]; Рис. 8: c) карта повреждений Палмгрена-Майнера после моделирования для того же примера, что и в таблице 1, с коэффициентом износа =0.5x10-11 [s];](https://evolution.skf.com/wp-content/uploads/sites/5/2019/06/wear-and-surface-fatigue-in-rolling-bearings-fig8c-1-850x486.jpg)