Контактная усталость при качении (RCF) – типичная причина выхода из строя подшипников качения и других подобных деталей механизмов. Фундаментальная теория RCF разработана Лундбергом и Палмгреном [1], [2]. Теория Лундберга и Палмгрена относилась главным образом к подповерхностной контактной усталости при качении и целиком опиралась на расчёты напряжений по Герцу для идеально гладких поверхностей. В отличие от контактной усталости при качении, поверхностная контактная усталость при качении включает в расчёт область, близкую к поверхности контакта (глубиной несколько микрометров), которая сильно подвержена воздействию локальных поверхностных напряжений, связанных с геометрическими особенностями поверхности: шероховатостью, отклонениями формы, вмятинами и т. д. Взаимодействие между смазочной плёнкой в эластогидродинамическом режиме смазывания (EHL) и повреждениями поверхности, определяющими места концентрации напряжений, очень важно для понимания явлений поверхностной усталости подшипников качения (Моралес-Эспехель и Габелли [3]). В этой статье исследовано развитие поверхностной контактной усталости при качении посредством моделирования контакта и взаимодействия с микроповреждениями поверхности, которые создают концентрации напряжения. Сравнение результатов численного моделирования с рядом экспериментальных результатов демонстрирует хорошую корреляцию, позволяя сформулировать гипотезу об основных механизмах поверхностной контактной усталости при качении, а также о возникновении и развитии такого усталостного разрушения в подшипниках качения. Эти новые знания хорошо согласуются с основной идеей обобщённой модели SKF для расчёта ресурса подшипников качения, которая различает поверхностное и подповерхностное усталостное разрушение [4], [5].

Теоретические исследования развития разрушений
Часто контактное усталостное разрушение, обусловленное поверхностным микроповреждением, развивается в выкрашивание. На распространение выкрашивания на поздних стадиях заметно влияют аспекты макрогеометрии, например, развитие геометрии контакта на дорожке качения и возникающая концентрация напряжения в подшипнике качения. Несколько исследователей изучали распространение выкрашивания в подшипниках качения, пытаясь связать воздействие механических аспектов на развитие разрушения.

В недавнем исследовании авторов данной статьи [6] с помощью моделирования и экспериментов изучалось распространение поверхностной контактной усталости при качении в подшипнике с предварительно нанесёнными вмятинами. Авторы пришли к выводу, что механизмы, характерные для работы шарикоподшипников, требуют учёта условий смазывания и взаимодействия напряжений между поверхностным и подповерхностным слоем, чтобы понять, почему развитие типичных клиновидных трещин вдоль дорожки качения отличается от начального поперечного развития разрушения в роликоподшипниках. В достаточной мере это объясняется лишь предположением о сухом трении качения.

Экспериментальные исследования развития разрушений
Снейр [7] в своём статистическом анализе надёжности подшипников рассматривал распространение выкрашивания в цилиндрическом роликоподшипнике, указывая на начальное развитие поперечного разрушения дорожки качения с последующим продольным распространением повреждения. На рис. 1 показаны экспериментальные испытания Снейра.

Современная точка зрения
Из теоретических и экспериментальных исследований, представленных в специализированной литературе, ясно прослеживаются две отличительных стадии развития выкрашивания из-за повреждений поверхности. Первая – достаточно медленное развитие поперечного разрушения дорожки качения, вторая – более быстрое продольное распространение повреждения. Поперечное распространение выкрашивания на дорожке качения в его начальной стадии может быть следствием более высокого напряжения на диаметрально противоположных краях повреждения, то есть в направлении, перпендикулярном качению, по сравнению с напряжениями на краях повреждения в продольном направлении.

Начальная стадия и развитие выкрашивания в шарикоподшипниках (рис. 2) и роликоподшипниках (рис. 3) разительно отличаются. Повреждения, возникшие на поверхности дорожек качения шарикоподшипников, первоначально развиваются клиновидно на заднем краю вмятины и быстро увеличиваются в направлении качения со скалыванием материала дорожки качения из клиновидной области. Развитие выкрашивания наблюдается в направлении качения, которое противоположно направлению трения и проскальзывания в этом месте (рис. 2). Выкрашивание в роликоподшипниках первоначально развивается на двух краях начального повреждения, разрастаясь поперёк дорожки качения, а потом в продольном направлении (рис. 3).

Цель данной статьи – дальнейшее изучение развития поверхностного усталостного разрушения роликоподшипников, а именно исследование с помощью моделирования механизма распространения разрушения, наблюдаемого в экспериментах. Данная статья является продолжением работы [3] о начальной стадии разрушения, но рассматривает вопросы распространения этого типа разрушения.

Экспериментальная часть
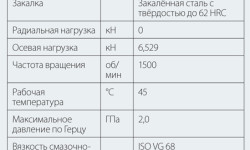
Эксперименты проводились на стандартных конических роликоподшипниках (см. табл. 1).

На конические роликоподшипники были искусственно нанесены вмятины шариковым индентором из карбида вольфрама диаметром 1 мм с использованием нагрузки вдавливания 1250 Н. Эта нагрузка обеспечивала получение вмятин диаметром 400 мкм, глубиной 30 мкм и высотой выступающего края 2 мкм. В рамках эксперимента было выполнено восемь вмятин, равномерно распределённых по окружности внутренних колец конических роликоподшипников. Вмятины также располагались с шагом 0,5 мм поперёк дорожки качения, начиная от её края. Однако в данной статье будет подробно рассматриваться только увеличение вмятин, расположенных в центре дорожки качения. В условиях эксперимента, приведённых в табл. 1, осевая нагрузка обеспечивала ширину контакта (по Герцу) в направлении качения приблизительно 142 мкм, что существенно меньше диаметра вмятины. Эксперименты проводились с разным количеством оборотов, чтобы наблюдать развитие усталостного разрушения, зависящего от концентрации напряжений и условий смазывания в области вмятин.

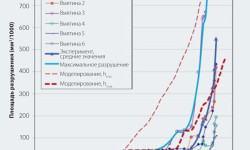
На рис. 4 представлены некоторые экспериментальные результаты развития выкрашивания вмятины в коническом роликоподшипнике при увеличении количества оборотов. Выкрашивание возникло на одной стороне вмятины, а затем распространилось на две стороны вмятины поперёк дорожки качения, то есть в направлении, перпендикулярном качению. На рис. 4(b) отмечен аппроксимированный эллипс контакта для сравнения с конечной стадией выкрашивания. Внутренние кольца нескольких подшипников периодически обследовались под микроскопом с интервалом приблизительно 5 млн оборотов, чтобы обнаружить начальную стадию выкрашивания и стадию его распространения. Каждую вмятину рассматривали под микроскопом и фотографировали для каждого значения количества оборотов. Начальное развитие и дальнейшее увеличение области выкрашивания вокруг вмятины измеряли с помощью цифровой обработки полученных микроснимков нескольких отдельных вмятин. Результаты этого детального исследования дали очень точную информацию о начальной стадии и последующем увеличении области выкрашивания с увеличением количества оборотов. Все собранные данные для шести отдельных вмятин с распространением повреждения показаны на рис. 5.

Более детальный анализ усреднённых данных испытаний показывает, что развитие области выкрашивания происходит в три этапа:

1. Инкубационный период от 50 до 60 млн оборотов, когда на дорожке качения не наблюдается никаких заметных разрушений. Этот период характеризует расчётный ресурс подшипника до появления признаков усталости.
2. Стадия начального развития разрушения, от 30 до 40 млн оборотов, как ожидалось, отражает экспоненциальный рост области повреждения.
3. Быстрое распространение. Эта стадия от 20 до 25 млн оборотов. В это время темп распространения повреждения существенно увеличивается (более чем вдвое по сравнению с предыдущим периодом).

Модель распространения повреждения
Расчёт разрушения при контакте качения выполняли, моделируя в первую очередь начальную вмятину на дорожке качения. Для этого использовали аналитическую параметрическую функцию, которая близко воспроизводит форму фактической вмятины.

Затем геометрия вмятины включалась в модель контакта перекатывания, чтобы воспроизвести циклическое напряжение по Герцу конкретного испытываемого подшипника. Расчёт развития разрушения выполняли, используя базовую модель поверхностной усталости и скалывания, которую ранее разработали Моралес-Эспехель и Бризмер [8] (в публикации дано полное описание). В эту модель были введены некоторые модификации. Например, порядок расчёта износа, описанный в исследовании [8], был исключён для ускорения численного моделирования. Модель быстрого смазывания исключена, и только модель сухого трения в зоне контакта используется для ситуаций, где начальная вмятина шире, чем контакт по Герцу в направлении качения (см. рис. 4a, моделирование конического роликоподшипника).

Модифицированная модель использована для расчёта всех величин давления и напряжения. Такая аппроксимация обоснована, потому что в данном случае смазочный материал, по всей вероятности, будет отводиться из вмятины и зоны контакта. В области края вмятины не ожидается воздействие гидродинамического давления, поэтому давление в этой области можно моделировать, используя гипотезу сухого трения в зоне контакта (игнорирование модели смазывания для шарикоподшипников с более широкой областью контакта по Герцу не допускается).Результаты вычисления величин давления в зоне контакта дают статистические данные напряжений для различных интервалов времени, заданных для данных испытаний (см. [5]). С помощью этого многоступенчатого процесса моделирования может быть рассчитана история усталостного напряжения для дальнейшей обработки с учётом критериев усталости, чтобы оценить усталостное разрушение, накопленное от начала испытания до текущего цикла нагружения. Эта схема точно следует методике обработки данных, которую разработали Моралес-Эспехель и Бризмер [8]. Общая степень повреждений, накопленных до текущего цикла нагружения, вычисляется по правилу Палмгрена-Майнера.

Когда усталостное разрушение достигает критического значения, возникает вероятность растрескивания материала. Текущая схема не имеет детальной модели распространения трещин, поэтому распространение разрушения моделируется просто удалением материала с выработанным усталостным ресурсом. С этой целью была реализована простая модель скалывания материала [8], которая выполняет задачу удаления материала с накопленным критическим разрушением и материала над ним. Эта модель использует также пороговую глубину (h) от поверхности, ниже которой материал с критическим разрушением не подлежит удалению. Значение пороговой глубины можно задать от h = 0 до h = ∞. Значение h ≥ 0 позволит удалять материал ниже поверхности. Данная модель не даст точных параметров развития разрушения, если параметр h не известен заранее или недоступны некоторые экспериментальные результаты, но она может очень хорошо описать диапазоны распространения разрушений, как будет показано ниже. Процесс расчёта повторяется для заданного количества циклов нагружения (до максимума, который обычно > 10⁹ циклов перекатывания), после чего выводится история развития разрушений.

Результаты моделирования
Данные испытаний приведены в табл. 1. В этом случае вмятины шире (диаметр 400 мкм), чем область контакта по Герцу в направлении качения (142 мкм), поэтому во время перекатывания будет невозможно развить необходимое давление в эластогидродинамическом режиме смазывания (EHL) на вмятине. Это вызовет разрыв смазочной плёнки на краю вмятины. В этих условиях влияние смазочной плёнки может быть исключено из анализа и развитие разрушения можно моделировать, просто используя сухое трение в зоне контакта.

На рис. 6 показано развитие выкрашивания от начальной вмятины с увеличением количества оборотов, а также представлено постепенное изменение давления по Герцу и соответствующих подповерхностных напряжений. Результаты численного моделирования наглядно показывают преобладающее направление развития области выкрашивания. Разрушение начинается с боковых краёв вмятины и распространяется в осевом направлении поперёк дорожки качения, что соответствует данным, полученным экспериментально (см. рис. 4). Вычисляя область повреждения и её расширение с увеличением количества оборотов подшипника, можно получить кривую развития области разрушения в зависимости от количества оборотов подшипников. Этот расчёт проводили для двух пороговых уровней глубины h, минимального и максимального, чтобы охарактеризовать объём моделирования (h_min касается только области максимального перпендикулярного напряжения сдвига вокруг вмятины, а h_max распространяется за её пределы). Результирующие кривые развития разрушения показаны пунктирными линиями на рис. 5. Тонкая пунктирная линия — результат минимальной настройки для оценки поверхностного микровыкрашивания (минимальное значение пороговой глубины). Следовательно, смоделированные результаты представляют собой безопасную границу разрушения, определяющую условия для максимальной ожидаемой области разрушения от любого поверхностного выкрашивания.

При задании максимальной пороговой глубины h развитие разрушения, показанное на рис. 5 жирной пунктирной линией, представляет собой более реалистичное соответствие экспериментальным результатам. Примечательно, что начальная тенденция расчётной области разрушения, которая указывает на пошаговое развитие, точно соответствует некоторым из экспериментальных измерений. Эта тенденция достигает устойчивого темпа роста между 90 и 120 млн оборотов. Можно сопоставить этот интервал с измеренной стадией начального увеличения вмятины (см. раздел «Экспериментальная часть»).

На рис. 7 показан темп увеличения разрушения по экспериментам в сравнении с результатами численного моделирования на уровне 11,5 млн оборотов (134 млн циклов). Хорошая корреляция между усреднёнными значениями экспериментальных результатов и результатами численного моделирования показывает возможность выявления численными методами некоторых важных механизмов поверхностной усталости и начального развития выкрашивания. Однако, экспериментальные результаты показывают быстрое распространение повреждения после 100 млн оборотов, которое не обнаружено численным моделированием. Возможное объяснение состоит в том, что формирование области выкрашивания приводит также к возникновению дополнительных нагрузок из-за динамической реакции подшипника на выкрашивание. В настоящее время эти дополнительные нагрузки не включены в модель. Таким образом, результаты численного моделирования могут быть применимы только в отношении начальной стадии выкрашивания.

В смоделированных результатах также интересен механизм развития разрушения. Поскольку вмятина немного шире, чем ширина контакта по Герцу в направлении качения, наиболее нагруженная зона на дорожке качения – боковая часть вмятины, где фактически начинается и развивается разрушение. Этот механизм распространения прослеживается и в численном моделировании, которое показывает, что боковой край выкрашивания испытывает наибольшие поверхностные давления и подповерхностные концентрации напряжения (рис. 6). Такая картина распространения выкрашивания, по всей видимости, является типичной для роликоподшипников.

Анализ и выводы
Эксперименты проводились на конических роликоподшипниках. На дорожки качения подшипников заранее были нанесены вмятины инструментом с заданной твёрдостью. Это создало ряд областей концентрации напряжений, в которых начиналось поверхностное выкрашивание, что давало возможность детального исследования его начальной стадии и стадии развития. Существующая модель для поверхностной усталости с учётом микрогеометрии (Моралес-Эспехель и Бризмер [8]) была адаптирована для изучения процесса поверхностного макровыкрашивания.

Модель была применена для достижения лучшего понимания стадии возникновения и начального распространения выкрашивания. Анализ расчётов показал, что численное моделирование действительно может хорошо объяснить многие экспериментальные наблюдения. В частности, экспериментальные результаты показали, что в случае конического роликоподшипника выкрашивание распространяется первоначально поперёк дорожки качения, то есть в направлении, перпендикулярном качению. В общем случае в подшипниках с линейным контактом наибольшие напряжения приходятся на боковые края вмятины. Эти повышенные напряжения стимулируют поперечное распространение повреждения во время его начальной стадии.

Из результатов данного исследования могут быть сделаны следующие выводы:

1. В подшипнике с предварительно нанесёнными вмятинами выкрашивание первоначально распространяется поперёк дорожки качения под воздействием повышенных напряжений на краях повреждения в направлении, перпендикулярном к направлению качения, как ранее было описано в литературе.

2. Представленная модель хорошо описывает два механизма распространения выкрашивания. В частности, для выкрашивания в роликоподшипниках получена хорошая корреляция между прогнозами моделирования и экспериментальными измерениями начального темпа распространения выкрашивания.

Благодарность
Проект получил частичное финансирование в рамках программы Европейской комиссии «Мария Кюри» по партнёрству и обмену специалистами между академическими и производственными организациями (IAPP) – проект iBETTER.

http://cordis.europa.eu/project/rcn/109976_en.html

Список литературы
[1] Lundberg, G. and Palmgren, A. (1947), “Dynamic Capacity of Rolling Bearings,” Acta Polytechnica, 1(3), pp 1–52.
[2] Lundberg, G. and Palmgren, A. (1952), “Dynamic Capacity of Roller Bearings,” Acta Polytechnica, 2(4), pp 96–127.
[3] Morales-Espejel, G. E. and Gabelli, A. (2011), “The Behavior of Indentation Marks in Rolling Sliding Elastohydrodynamically Lubricated Contacts,” Tribology Transactions, 54, pp 589–606.
[4] Morales-Espejel, G.E., Gabelli, A. de Vries A. (2015), “A Model for Rolling Bearing Life with Surface and Subsurface Survival – Tribological Effects”, to be published at Tribology Transactions.
[5] Morales-Espejel, G.E. and Gabelli, A. (2015), “The SKF Generalized Bearing Life Model – the power of tribology,”
Evolution #4-2015, pp 22-28.
[6] Morales-Espejel, G.E. and Gabelli, A. (2015), “The Progression of Surface Rolling Contact Fatigue Damage of Rolling Bearings with Artificial Dents,” Tribology Transactions, 58, pp 418–431.
[7] Snare, B. (1970), “How Reliable Are Bearings?” The Ball Bearing Journal, 162, pp 3–7.
[8] Morales-Espejel, G. E. and Brizmer, V. (2011), “Micropitting Modelling in Rolling–Sliding Contacts: Application to Rolling Bearings,” Tribology Transactions, 54, pp 625–643.