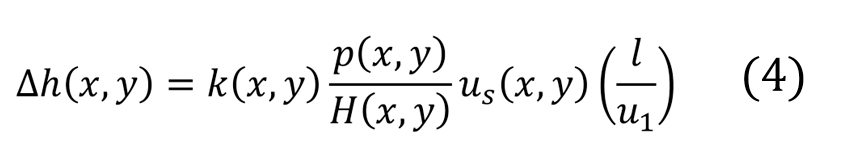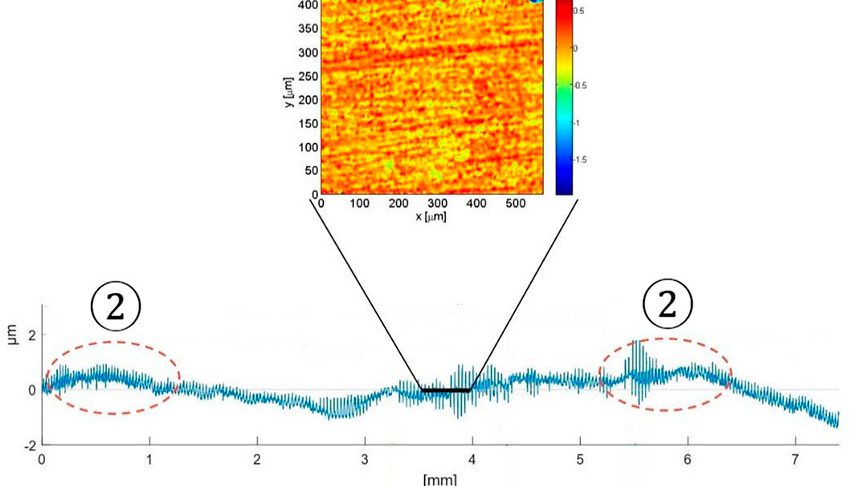
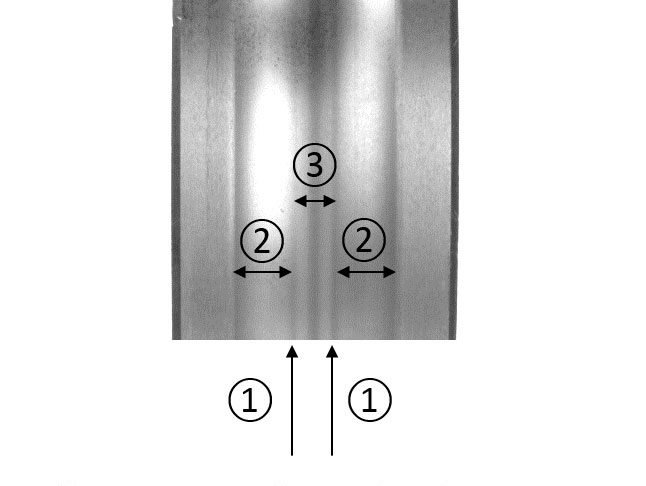
Los rodamientos que funcionan bajo condiciones de lubricación deficiente en situaciones de contacto deslizante irregular, o con la presencia de partículas abrasivas o contaminación de líquidos, pueden sufrir modificaciones sustanciales en los perfiles de los caminos de rodadura (fig. 1). Con el tiempo, esas modificaciones pueden desarrollar concentraciones de tensión en las zonas más cargadas (fig. 2), que potencialmente pueden conducir a un incremento en la fatiga superficial localizada, y producir franjas de microdesconchado o desconchado en los caminos de rodadura en las zonas de mayor tensión (fig. 3). Esta forma de daños potenciales puede afectar a cualquier rodamiento, pero las aplicaciones más afectadas serán las que tengan una presencia de gran contaminación, corrosión, lubricación deficiente y deslizamiento irregular o carga variable. Pueden encontrarse ejemplos de ello en la industria minera, papelera, en aplicaciones eólicas y en otros sectores.

El desgaste en los rodamientos es un fenómeno no lineal, e incluso observaciones y mediciones a intervalos regulares del desgaste muestran que la simple intuición no basta para predecir como evolucionará el desgaste con el tiempo. Esto se debe a diversas causas; el desgaste depende principalmente del deslizamiento y de la carga local, y el desgaste propiamente dicho modifica estos dos factores, por lo que no es posible una simple extrapolación. Entonces es necesario un análisis más riguroso, y es por ello que SKF ha dedicado mucho esfuerzo en la investigación del deslizamiento y del desgaste en los rodamientos y de los efectos en su vida útil [1].

Todo rodamiento sufre un cierto grado de deslizamiento; es algo normal. Lo produce su geometría interna y/o las condiciones de carga. Por ejemplo, un rodamiento de bolas o rodillos radial, perfectamente cargado radialmente, también tendrá deslizamiento (deslizamiento de Heathcote) debido a la geometría de contacto entre el elemento rodante y el aro, y a la deformación elástica por la carga (figs. 4a y 4b). Debido a que el desgaste depende del deslizamiento, con el tiempo (si las condiciones dadas fueran correctas), podría esperarse que las franjas causadas puramente por rodadura (A y A¹) serían las únicas zonas donde no se produciría desgaste y, por tanto, las únicas que soportarían toda la carga en el contacto.

Afortunadamente, esto solo podría pasar en situaciones de intenso desgaste, como en presencia de partículas abrasivas, intensa corrosión o deslizamiento anormal a causa de una carga o montaje inapropiados del rodamiento. En la mayoría de los casos, los rodamientos funcionan adecuadamente, y este deslizamiento será el entorno de trabajo normal de un rodamiento sin problemas.

En el presente artículo, queremos abordar con mayor profundidad los mecanismos principales del modo de daño causado por la potencial combinación de desgaste/fatiga: la modelización y los experimentos desarrollados para comprenderlos mejor y arrojar alguna luz sobre los métodos de prevención.

Modelización

Modelización del desgaste

En [2], se debaten diferentes modelos de desgaste bajo condiciones de lubricación, y se llega a la conclusión de que, en todos los casos, pueden representarse por un modelo de Archard [3], a veces con un sofisticado modelo de coeficiente de desgaste. En la mayoría de los casos, el coeficiente de desgaste es un factor empírico basado en experimentos. Por ello, la ecuación de desgaste más general es:

Donde:
V = volumen de desgaste [m³] en un cierto tiempo,
= coeficiente de desgaste de Archard adimensional [-],
F = fuerza de contacto [N],
H = dureza actual de la superficie del material [Pa],
s = distancia de deslizamiento [m] en un cierto tiempo.

El volumen de desgaste puede expresarse como:

Donde:
h = espesor de capa superficial arrancada [m] en un cierto tiempo,
A_s = zona de deslizamiento [m²] en un cierto tiempo.

Por tanto, sustituyendo (2) en (1) y teniendo en cuenta que la presión media de contacto :

Ahora, teniendo en cuenta el tiempo total de contacto  por ciclo de carga, que representa el tiempo de paso de las dos superficies deslizantes por la zona de contacto a la velocidad de deslizamiento, entonces la zona de deslizamiento es simplemente la zona de contacto, por tanto A_s = A. El espesor de la capa arrancada por número de rodaduras (N) puede calcularse siguiendo [2] como:

Donde:
u_s = la velocidad de deslizamiento local [m/s]
u₁ = la velocidad media de la superficie analizada [m/s]
l = la longitud de contacto a lo largo del sentido de deslizamiento [m].

Obsérvese que casi todas las cantidades son locales (x,y.) Aquí también la dureza del acero en los caminos de rodadura y elementos rodantes se supondrá constante. La ecuación (4) da el espesor local de la capa desgastada arrancada por cada rodadura en un contacto de rodamiento.

Modelización de la interacción desgaste/fatiga

Para modelizar la interacción desgaste/fatiga en rodamientos, se necesita aplicar un modelo de fatiga por contacto de rodadura (RCF) en cada paso sobre el camino de rodadura con un perfil modificado previamente (en ambas superficies) debido al desgaste; de este modo, se produce la interacción de ambos fenómenos (desgaste y fatiga). Cada vez que el desgaste modifica el perfil, en el contacto es preciso calcular una nueva distribución de la presión para el modelo de fatiga. Dicho proceso refleja lo que sucede en la vida real. Sin embargo, esto es muy costoso desde el punto de vista computacional, teniendo en cuenta que la vida útil típica de RCF puede abarcar millones de rodaduras. Por ello, existen simplificaciones que reducen sustancialmente el costo computacional:
 

1. Se aplica un cálculo de contacto seco en lugar de una solución de lubricación elastohidrodinámica (EHL) completa, y se evita en este caso la solución del problema de lubricación considerando sencillamente un coeficiente de fricción fijo (medido).
2. Se actualiza el perfil resultante del desgaste cada cierto número de rodaduras en lugar de actualizarlo por cada rodadura.
3. El punto número (2) también tiene como consecuencia que la actualización del cálculo del contacto y el cálculo de los daños (fatiga) también puede hacerse al mismo tiempo que la actualización del perfil por el desgaste, en lugar de hacerlo en cada rodadura.

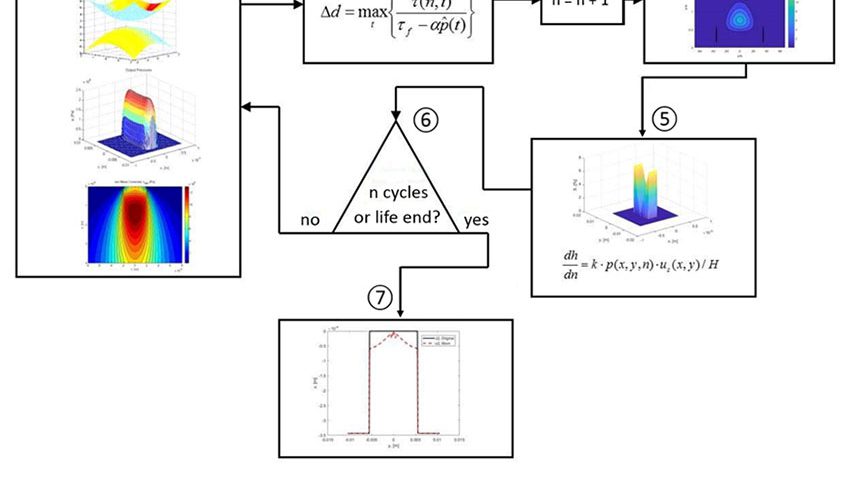
El organigrama de la fig. 5 muestra un resumen del procedimiento de cálculo. Obsérvese que, en este caso, se usa el criterio de fatiga de Dang Van [4] y la acumulación de daños se realiza mediante la ley lineal de Palmgren-Miner [5,6]. Pero si los experimentos hubieran sugerido esto, podría haberse usado cualquier otro criterio de fatiga y carga de acumulación de daños.

Experimentos

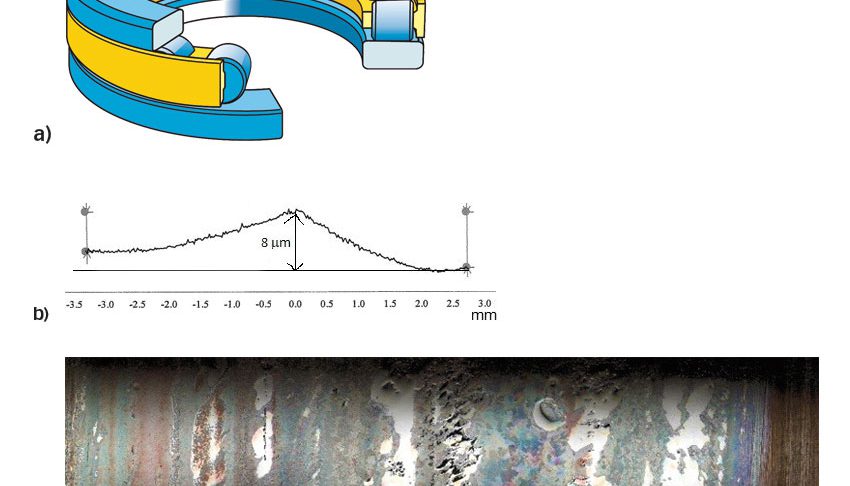
Para validar el modelo de fatiga, se realizó una prueba de resistencia utilizando un rodamiento axial de rodillos cilíndricos 81107 TN (fig. 6a), cargado axialmente con C/P = 6,5 y condiciones de lubricación dadas por un ≈ 0.5.

Antes de la prueba, se elaboró un perfil artificial (fig. 6b) en los rodamientos nuevos, como si hubieran estado funcionando bajo condiciones de desgaste duras. Durante la prueba, algunos rodamientos sufrieron fallas, principalmente a causa de daños en los rodillos (fig. 6c), por lo que el modelo de vida útil pudo compararse con los resultados de la prueba corta. En el modelo de la fig. 5, se tuvieron en cuenta exactamente los mismos rodillos desgastados y arandelas nuevas; los resultados mostraron muy buena concordancia con el límite inferior de la vida útil L₁₀ medida, teniendo en cuenta la estadística de Weibull.

Paralelamente, también se realizaron pruebas y mediciones de desgaste en rodamientos completos para calcular el coeficiente de desgaste y validar luego el modelo usando diferentes conjuntos de experimentos. La concordancia entre el modelo y los experimentos también fue satisfactoria.

Resultados

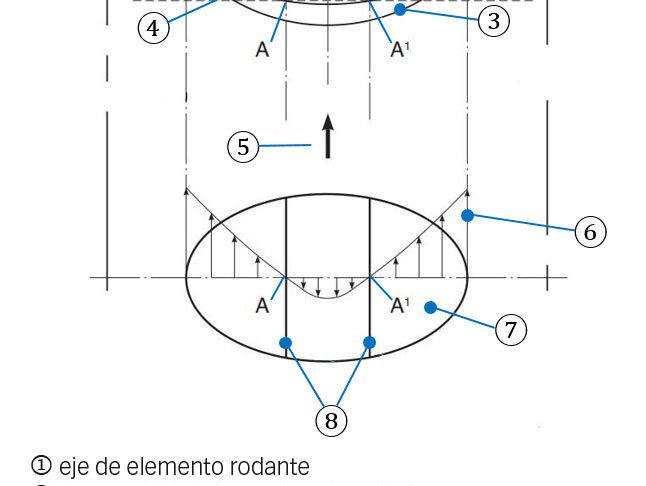
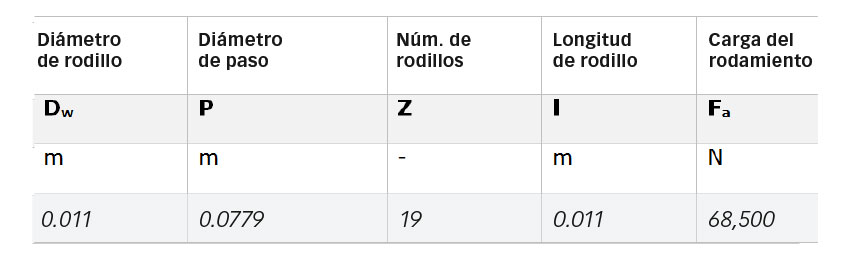
En los rodamientos axiales de rodillos cilíndricos, el deslizamiento varía (disminuye) linealmente desde los dos bordes del rodillo hacia la línea de paso, donde el deslizamiento es cero (fig. 7). Hacia el diámetro exterior del rodamiento, el rodillo será la superficie más rápida, y hacia el diámetro interior, será la más lenta. Para ilustrar los efectos coincidentes del desgaste y la fatiga en un rodamiento con deslizamiento variable transversalmente al camino de rodadura, se contempla un caso de un rodamiento axial de rodillos de mayor tamaño (81212 TN), tal como se describe en los datos de la Tabla 1.

Se creó una simulación que permitía al modelo modificar el perfil resultante del desgaste con coeficiente de desgaste dimensional (definido como ) con las condiciones de carga tal como se indican en la Tabla 1 y la simulación prevista para alcanzar nominalmente 300 millones de rodaduras.

En lugar de actualizar los perfiles de desgaste por cada rodadura, para ahorrar tiempo computacional sin perder precisión, se comprobó que las actualizaciones podían hacerse cada 15,5 millones de rodaduras del rodillo. Para la simulación, se aplica el mismo modelo representado en la fig. 5, incluido el modelo de desgaste Archard de la ecuación (4).

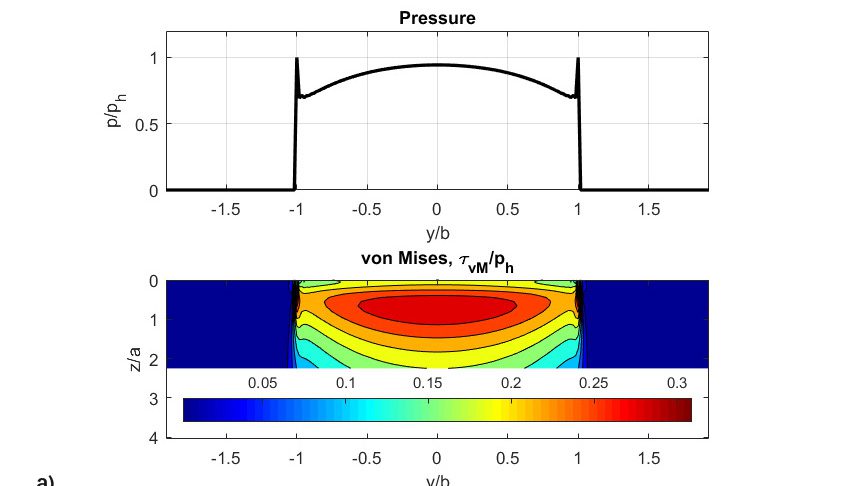
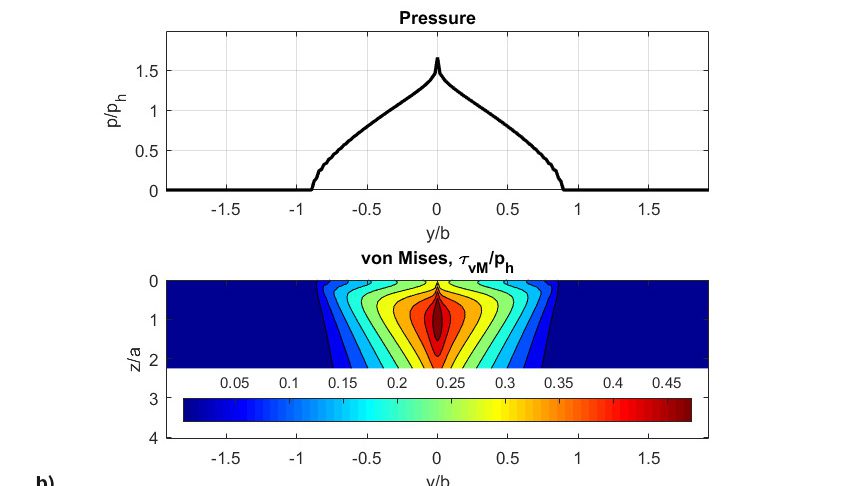
Los resultados de la simulación se muestran en la fig. 8. La figura muestra:
 

1. las presiones adimensionales,
2. los esfuerzos cortantes de von Mises,
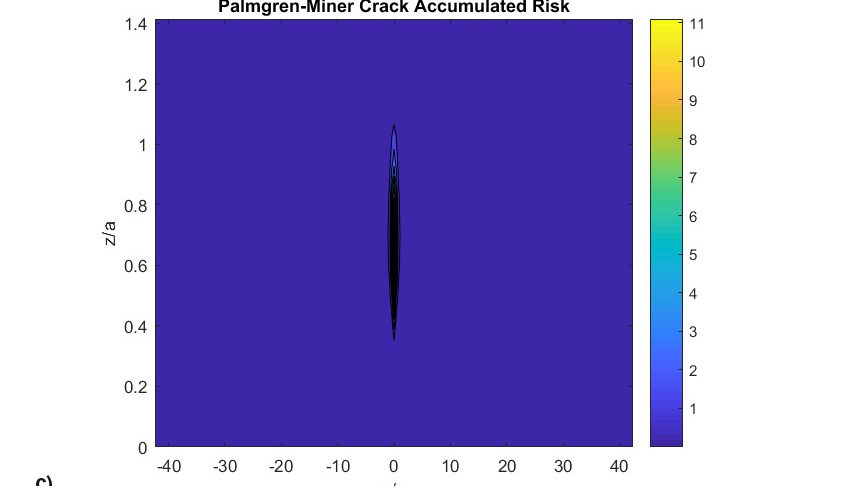
3. el mapa de daños,
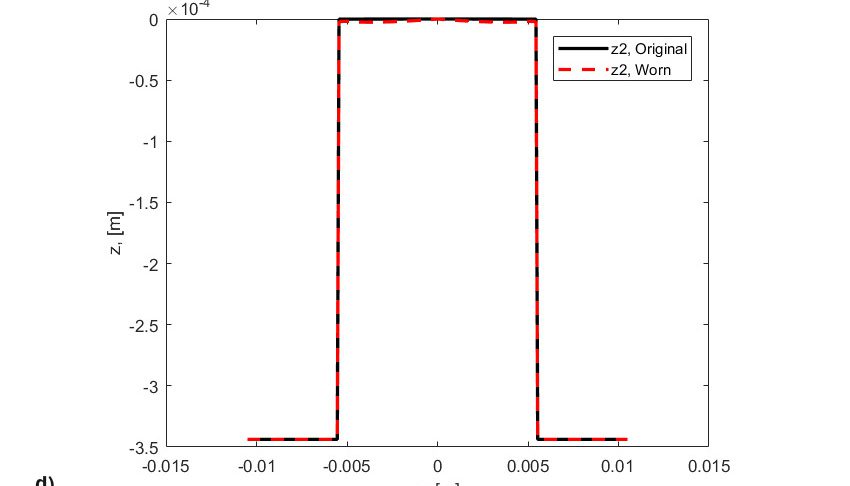
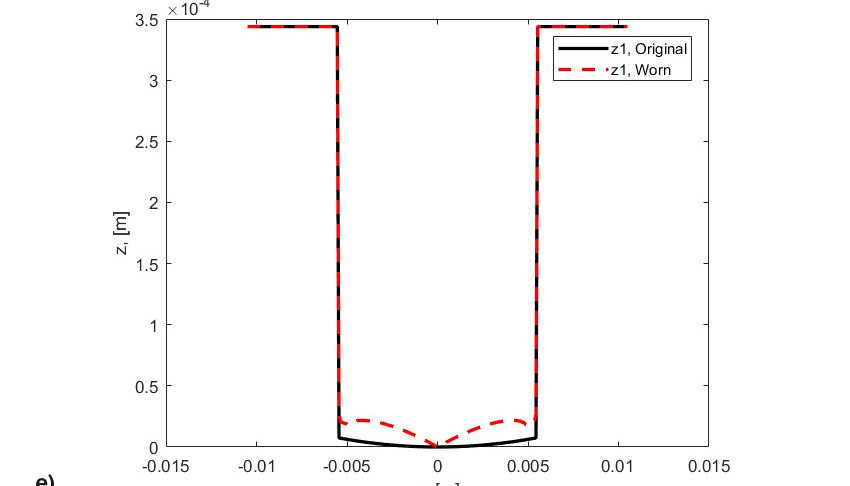
4. los perfiles originales de rodillo y arandela,
5. los perfiles de desgaste de rodillo y arandela, que corresponden al período del final de las simulaciones.

Hay que señalar que el mapa de daños alcanzó un valor de daños totales superior a 1 (umbral de iniciación de grietas) tras solo 31 millones de rodaduras. Los resultados mostrados en la fig. 8 están relacionados con los pasos de simulación inicial y final. La presión inicial (fig. 8a) en la primera rodadura parece más o menos herciana, pero muestra algún efecto de tensión en el borde debido a que se utilizó un perfil de rodillo recto simple en lugar de un rodillo perfilado adecuado que evitaría esas tensiones en el borde. A partir de los resultados, es evidente que el deslizamiento en la línea de paso es cero; asimismo, la parte de la simulación del modelo de desgaste de Archard indica cero desgaste en esa ubicación.

De hecho, el desgaste está vinculado a la distribución del deslizamiento a través del camino de rodadura. De este modo, se producirá desgaste a un ritmo creciente a medida que nos alejamos de la línea de paso del camino de rodadura. Obsérvese que originalmente la presión de contacto era casi rectangular (fig. 8a), pero a medida que se va arrancando material de los dos lados del contacto de rodadura, la presión se reduce en las zonas de gran deslizamiento, y aumenta fuertemente y se concentra en la zona de cero deslizamiento (línea de paso), (fig. 8b). Este aumento de presión produce grandes tensiones y fatiga a un ritmo más rápido hasta que se desarrolla una falla en el centro del rodillo (fig. 8c). En realidad, el efecto simultáneo y coincidente de desgaste y fatiga puede acelerar el desconchado de RCF en el contacto. Este desconchado acelerado por fatiga no está relacionado con tensión por fricción inducida en el deslizamiento, sino que es más bien el resultado de la modificación del perfil original de los cuerpos rodantes (figs. 8d y 8e), lo cual conduce a un incremento pronunciado en la tensión de contacto y menor espesor localizado de película lubricante.