La fatiga de contacto rodante (Rolling contact fatigue, RCF) es una forma de falla típica en rodamientos y componentes de tipo similar en máquinas. El trabajo fundamental en RCF lo realizaron Lundberg y Palmgren [1], [2]. La teoría de Lundberg-Palmgren estaba enfocada principalmente en la fatiga de contacto rodante en la subsuperficie y se basaba exclusivamente en cálculos de tensiones hercianas de una suavidad ideal. Sin embargo, la fatiga de contacto rodante en las superficies (Surface rolling contact fatigue, SRCF) involucra una zona cerca de la superficie de contacto (de una profundidad de unas pocas micras) que es intensamente afectada por la tracción superficial local y las tensiones originadas por las características geométricas de la superficie, como aspereza, desviaciones del perfil, indentaciones, etc. La interacción entre la película lubricante elastohidrodinámica (elasto-hydrodynamic lubricating, EHL) y las respectivas características que determinan incrementos de tensiones en la superficie es muy importante para comprender el fenómeno de fatiga en la superficie de los rodamientos (Morales-Espejel y Gabelli [3]). En este artículo, el desarrollo de la SRCF se investiga modelizando el contacto y la interacción, con desviaciones en la microgeometría de la superficie que generan concentraciones de tensiones. La comparación de simulaciones numéricas con un conjunto de resultados experimentales indica una buena correlación, que permite formular una hipótesis sobre los mecanismos subyacentes de la SRCF, al igual que su comienzo y crecimiento en los rodamientos. Este nuevo conocimiento se corresponde muy bien con la idea básica detrás del modelo generalizado de vida útil de rodamientos (Generalized Bearing Life Model, GBLM) de SKF, que separa los daños por fatiga de la superficie de los de la subsuperficie [4][5].

Investigación teórica en el desarrollo de los daños
Frecuentemente, los daños por fatiga de contacto rodante originados alrededor de las características de microgeometría de la superficie se convierten en desconchado. En su forma avanzada, la propagación del desconchado está poderosamente influida por aspectos de macrogeometría: por ejemplo, la evolución de la geometría de contacto de los caminos de rodadura y el campo de tensiones general resultante en un rodamiento. Varios investigadores han estudiado la propagación del desconchado en rodamientos en un intento de asociar los aspectos mecánicos que impulsan el desarrollo de los daños.

Una investigación reciente realizada por los autores de este artículo [6] ha estudiado la propagación de la SRCF en rodamientos preindentados, tanto con un modelo como con experimentos. La conclusión a la que se ha llegado es que los mecanismos que intervienen en los rodamientos de bolas exigen tener en cuenta las condiciones de lubricación y la interacción de tensiones entre la superficie y la subsuperficie para comprender el desarrollo de grietas típicas en forma de V a lo largo del camino de rodadura, de manera diferente del crecimiento de los daños transversales iniciales observados en rodamientos de rodillos, que pueden explicarse lo suficientemente solo con suposiciones de contacto seco.

Observaciones experimentales en el desarrollo de los daños
Snare [7], en su análisis estadístico de la confiabilidad de los rodamientos, monitoreó la propagación del desconchado en un rodamiento de rodillos cilíndricos, y mostró el claro desarrollo de los daños transversalmente al camino de rodadura antes de que el desconchado empezara a propagarse a lo largo de este. La fig. 1 muestra las pruebas experimentales de Snare.

Conocimientos actuales
De la investigación teórica y experimental que puede encontrarse en la bibliografía, se observan como mínimo dos fases de propagación del desconchado distintivas a partir de defectos en la superficie. La primera es cuando el desconchado crece transversalmente al camino de rodadura a un ritmo más o menos lento, y la segunda es cuando el crecimiento a lo largo del trayecto de rodadura es de una forma más acelerada. Los motivos de la propagación del desconchado transversalmente al camino de rodadura en su fase inicial se interpretan como una consecuencia de las tensiones más elevadas presentes en los bordes diametrales del desconchado; es decir, a lo largo de la dirección ortogonal de rodadura, en comparación con las tensiones en los bordes de ataque y de salida del desconchado.

El comportamiento del comienzo y la propagación del desconchado en los rodamientos de bolas (fig. 2) y de rodillos (fig. 3) es sorprendentemente nítido. Los desconchados iniciados en la superficie de los rodamientos de bolas se desarrollan inicialmente con una forma en V característica en el borde de salida de la indentación, y crecen rápidamente en la dirección de rodadura con el desprendimiento de material del camino de rodadura de la zona en forma de V. El crecimiento del desconchado se observa en la dirección de rodadura, que es la dirección opuesta a la de fricción y de deslizamiento existente en este lugar (fig. 2). Los desconchados iniciados en la superficie de los rodamientos de rodillos se propagan inicialmente en ambos lados del punto de comienzo original, y crecen transversalmente antes de extenderse a lo largo del camino de rodadura (fig. 3).

El objetivo de este artículo es dar más precisiones sobre el desarrollo de los daños por fatiga iniciados en la superficie de los rodamientos de rodillos. La intención es comprender, a través de modelos, los mecanismos que impulsan la propagación de los daños tal como se ha observado en los experimentos, como continuación de la labor presentada por los autores [3], sobre la fase de daños inicial, aunque enfocada ahora en la propagación de esos daños.

Labor experimental
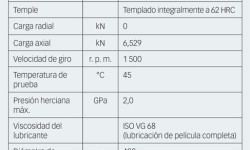
Se han realizado experimentos con rodamientos de rodillos cónicos estándares; ver la tabla 1.

En ellos, se realizaron indentaciones artificiales utilizando una carga de indentación de 1 250 N y un indentador de bola de carburo de tungsteno de 1 mm de diámetro. Esta carga produce indentaciones con un diámetro de 400 µm, una profundidad de 30 µm y una altura de borde elevado de unos 2 µm. El experimento consistió en ocho indentaciones equidistantes entre sí alrededor de la circunferencia del aro interior de los rodamientos de rodillos cónicos. Las indentaciones también se espaciaron a pasos de 0,5 mm transversalmente al camino de rodadura, empezando desde el borde de este. No obstante, en el presente artículo, solo se abordará con detalle el desarrollo de los daños en las indentaciones situadas en el centro del camino de rodadura. Con las condiciones operativas dadas en la tabla 1, la carga axial proporcionaba un ancho herciano en la dirección de rodadura de unos 142 µm, lo cual es un valor sustancialmente menor en comparación con el diámetro de la indentación. Los experimentos se ejecutaron a diferentes números de revoluciones para observar el desarrollo de los daños por fatiga resultantes de la concentración de tensiones y las condiciones de lubricación de las indentaciones.

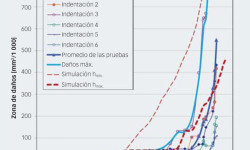
La fig. 4 muestra algunos resultados experimentales sobre el desarrollo del desconchado de la indentación en el rodamiento de rodillos cónicos al aumentar el número de revoluciones. El desconchado se inició en un lado de la indentación y luego aumentó hacia los dos lados de esta transversalmente al camino de rodadura, es decir, a lo largo de la dirección ortogonal a la rodadura. En la fig. 4 (b), se ha trazado una elipse de contacto aproximada para comparar con el desconchado final. Varios aros interiores se monitorearon mediante una inspección periódica con microscopio realizada en cada rodamiento, con una separación de aproximadamente 5 millones de revoluciones, para detectar la fase de iniciación y propagación del desconchado. Cada indentación se inspeccionó y fotografió en el microscopio en función del número de revoluciones realizado en la prueba. El desarrollo inicial y el posterior crecimiento de la zona desconchada alrededor de la indentación se midieron procesando digitalmente fotografías del microscopio de varias indentaciones individuales. Los resultados de esta investigación detallada brindaron información muy precisa sobre el crecimiento inicial y progresivo de la zona de daños por desconchado con respecto al número de revoluciones. Todos los datos recogidos de las seis indentaciones individuales que desarrollaron daños por desconchado se muestran en la fig. 5.

Una inspección más detallada de los datos medios de la prueba indican que el desarrollo de la zona desconchada sigue un proceso de tres etapas:

1. Un tiempo de incubación de 50 a 60 millones de revoluciones en el que no pueden detectarse daños visibles aparentes en el camino de rodadura del rodamiento; esto es aproximadamente la vida de fatiga nominal del rodamiento.
2. La fase de desarrollo inicial de los daños, que se extiende de 30 a 40 millones de revoluciones, muestra, tal como se prevé, un crecimiento exponencial de la zona dañada.
3. El crecimiento acelerado. Se extiende de 20 a 25 millones de revoluciones, durante las cuales el ritmo de crecimiento aumenta sustancialmente (más del doble en comparación con el período anterior).

Modelo de propagación de los daños
El cálculo de los daños en el contacto rodante se realiza primordialmente modelizando la indentación inicial del camino de rodadura. Esto se lleva a cabo utilizando una función analítica paramétrica que reproduce estrechamente la forma de la indentación real.

La geometría de la indentación se incluye luego en un modelo de contacto de rodadura para reproducir la tensión cíclica herciana del rodamiento de prueba real. El cálculo del desarrollo de los daños se efectúa utilizando la fatiga básica de la superficie y el modelo de desprendimiento desarrollado anteriormente por Morales-Espejel y Brizmer [8], completamente descrito aquí. No obstante, también se introdujeron algunas modificaciones y adaptaciones. Por ejemplo, el procedimiento del cálculo del desgaste, tal como se describe en [8], se desconectó para acelerar la velocidad de las simulaciones numéricas. El modelo de lubricación rápido se desconecta, y solo se usa el modelo de contacto seco en situaciones en donde la indentación inicial es más amplia que el contacto herciano en la dirección de rodadura, que es el caso de simulación con rodamientos de rodillos cónicos de la fig. 4(a). Luego el modelo se usa para el cálculo de las presiones y tensiones generales. Esta aproximación es válida debido a que, en este caso, es probable que el lubricante se escape de la indentación y el contacto. No es de esperar que se genere presión hidrodinámica en la región del borde de la indentación, cuyas presiones, por tanto, pueden modelizarse entonces utilizando la hipótesis de contacto seco (para rodamientos de bolas con una zona de contacto herciana más ancha, no puede ignorarse el modelo de lubricación).

Una vez calculadas las presiones de contacto, se obtiene el historial de tensiones de una serie de etapas cronológicas diseñadas para simular el paso de la indentación a través del contacto rodante (ver [5]). A partir de este proceso de simulación multietapa, el historial de tensiones de fatiga puede calcularse para el posterior procesado del criterio de fatiga, a fin de calcular los daños por fatiga acumulados desde el inicio del ciclo de carga actual. Este esquema sigue exactamente el mismo procesamiento de datos introducido por Morales-Espejel y Brizmer [8]. Los daños totales acumulados hasta el ciclo de carga actual se calculan siguiendo la regla de Palmgren-Miner.

Cuando la fatiga alcanza un valor de daños crítico, surge la posibilidad de un comienzo de la fracturación del material. El esquema actual no tiene un modelo de propagación de grietas detallado; la propagación de los daños se simula simplemente retirando el material producido por la fatiga. Para este fin, se implementó un modelo simple de desprendimiento de material [8] que realiza la tarea de retirar el material con daños críticos acumulados y el material sobre este. Este modelo también contiene una profundidad umbral (h) de la superficie, por debajo de la cual no se permite que se desprenda material con daños críticos. Esta profundidad umbral puede seleccionarse desde h = 0 a h = ∞. Al seleccionar h = 0, se permitirá que se desprenda material debajo de la superficie. El modelo actual no puede dar una indicación precisa del crecimiento de los daños si el parámetro h no se conoce previamente o si no se dispone de algunos resultados experimentales, pero puede describir muy bien los rangos de crecimiento de los daños tal como se mostrará abajo. El proceso de cálculo se repite para un número dado de ciclos de carga (hasta un valor máximo, por lo general > 10⁹ ciclos de rodadura), tras lo cual se notifica el historial de desarrollo de los daños.

Resultados del modelo
En la tabla 1, se muestran los datos de la prueba. En este caso, las indentaciones son más anchas (es decir, 400 µm de diámetro) que en el contacto herciano en la dirección de rodaje (es decir, 142 µm); por tanto, es imposible que durante el rodaje se desarrolle la presión de EHL requerida sobre la indentación. Esto inducirá un colapso de la película de aceite en el borde de la zona indentada. En estas condiciones, el efecto de la película lubricante puede excluirse del análisis, y el desarrollo de los daños puede simularse simplemente utilizando la aproximación del contacto seco.

La fig. 6 muestra la evolución del desconchado a partir de la indentación inicial para un número de revoluciones en incremento; también muestra los cambios progresivos de la presión herciana y tensiones subsuperficiales relacionadas. Los resultados de las simulaciones numéricas muestran claramente la dirección preferencial del desarrollo de la zona desconchada. Los daños empiezan a partir de los bordes laterales de la indentación y aumentan en dirección axial transversalmente al camino de rodadura de manera similar a la observada en los experimentos (ver la fig. 4). Al calcular la zona abarcada por los daños y su evolución con el número de revoluciones del rodamiento, es posible obtener la curva del desarrollo de la zona de los daños respecto del número de revoluciones de los rodamientos. Esto se ha calculado para dos niveles de profundidad umbral, h, un mínimo y un máximo, para caracterizar el alcance de las simulaciones con modelos (h_mín tocando justo la zona de máximo esfuerzo cortante alrededor de la indentación, y h_máx muy apartada de ella). Las curvas del desarrollo de daños resultantes se muestran con líneas discontinuas en la fig. 5. Una línea discontinua delgada es el resultado de la disposición más conservadora para calcular el microdesconchado iniciado en la superficie; es decir, el valor mínimo de la profundidad umbral. Por consiguiente, los resultados simulados representan un límite seguro de los daños, que definen las condiciones de la zona de daños máxima prevista de cualquier desconchado iniciado en la superficie.

Con la implementación de un valor de profundidad umbral máxima, h, la evolución de los daños expuesta en la fig. 5 con una línea discontinua gruesa muestra una adaptación más realista con los resultados experimentales. Es evidente la tendencia inicial de la zona de daños calculada, que muestra un desarrollo gradual que se adapta claramente a algunas de las mediciones experimentales. Esta tendencia logra un ritmo de crecimiento estable de entre 90 y 120 millones de revoluciones, intervalo que puede compararse con la fase de desarrollo inicial medida del crecimiento de los daños de la indentación, tal como se ha analizado en la sección “Labor experimental”.

La fig. 7 muestra el ritmo de crecimiento de los daños de los experimentos en comparación con el valor obtenido de simulaciones numéricas, que es de 11,5 millones de revoluciones (134 millones de ciclos). Esta buena correlación entre el promedio de los resultados experimentales y las simulaciones numéricas muestra la capacidad del cálculo para captar algunos de los principales efectos de los mecanismos de fatiga de la superficie y del desarrollo inicial del desconchado. Además, los resultados experimentales indican un crecimiento acelerado después de 100 millones de revoluciones, que parece faltar en los resultados de las simulaciones numéricas. Una posible explicación de este comportamiento es que la generación de una zona desconchada también da como resultado cargas adicionales debidas a la respuesta dinámica del rodamiento a los daños de desconchado. Por el momento, estas cargas adicionales no están incluidas en el modelo; por ello, con las simulaciones numéricas solo es razonable comparar los daños de desconchado iniciales.

En los resultados simulados, también es interesante el mecanismo del desarrollo de los daños. Debido a que la indentación es algo mayor que el ancho herciano en la dirección de rodadura, la zona con más carga del camino de rodadura es la zona lateral de la indentación, donde de hecho se inician y desarrollan los daños. Este mecanismo de propagación también puede encontrarse en la simulación numérica en la que se muestra el borde lateral del desconchado afectado por las presiones más elevadas en la superficie y concentraciones de tensiones en la subsuperficie (fig. 6). Este tipo de propagación del desconchado parece ser típico de los rodamientos de rodillos.

Comentarios y conclusiones
Se han realizado experimentos en rodamientos de rodillos cónicos. En sus caminos de rodadura, se hicieron indentaciones con marcas de dureza predefinidas. Esto creó una serie de incrementadores de tensiones en la superficie que originaron en ella desconchados, lo que permitió un estudio detallado de su comienzo y desarrollo. Se adaptó un modelo existente de fatiga de microgeometría de las superficies (Morales-Espejel y Brizmer [8]; es decir, deformación superficial) para estudiar el proceso de macrodesconchado iniciado en la superficie.

El modelo se aplicó para comprender mejor el inicio y la fase de propagación prematura del desconchado. De los resultados de los cálculos, se ha averiguado que de hecho el modelo numérico puede simular y explicar bien muchas de las observaciones experimentales. Los resultados experimentales sobre todo han indicado que, en el caso de los rodamientos de rodillos cónicos, el desconchado inicialmente se propaga transversalmente al camino de rodadura, es decir, a lo largo de la dirección ortogonal a la rodadura. En general, en rodamientos de contacto en línea, las tensiones son superiores en los bordes laterales de la indentación. Estas tensiones más elevadas impulsan el crecimiento del desconchado transversalmente al camino de rodadura durante su expansión inicial.
De los resultados de la labor actual, pueden extraerse las siguientes conclusiones:

1. Los rodamientos de rodillos preindentados propagan el desconchado inicialmente en forma transversal al camino de rodadura, impulsados por las tensiones más elevadas que se hallan en los bordes del desconchado a lo largo de la dirección ortogonal a la rodadura, tal como antes se ha descrito en la bibliografía.

2. El modelo presentado constituye una buena descripción de los dos mecanismos de propagación del desconchado. Sobre todo en los desconchados de los rodamientos de rodillos, su ritmo de crecimiento inicial hace que se observe una buena correlación entre la predicción del modelo y las mediciones experimentales.

Agradecimientos
El citado proyecto fue financiado en parte por la Comisión Europea, Marie Curie Industry-Academia Partnerships and Pathways (IAPP) – Proyecto iBETTER.

http://cordis.europa.eu/project/rcn/109976_en.html

Referencias
[1] Lundberg, G. y Palmgren, A. (1947), “Dynamic Capacity of Rolling Bearings,” Acta Polytechnica, 1(3), págs. 1–52.
[2] Lundberg, G. y Palmgren, A. (1952), “Dynamic Capacity of Roller Bearings,” Acta Polytechnica, 2(4), págs. 96–127.
[3] Morales-Espejel, G. E. y Gabelli, A. (2011), “The Behavior of Indentation Marks in Rolling Sliding Elastohydrodynamically Lubricated Contacts,” Tribology Transactions, 54, págs. 589–606.
[4] Morales-Espejel, G.E., Gabelli, A. de Vries A. (2015), “A Model for Rolling Bearing Life with Surface and Subsurface Survival – Tribological Effects”, que se publicará en Tribology Transactions.
[5] Morales-Espejel, G.E. y Gabelli, A. (2015), “The SKF Generalized Bearing Life Model – the power of tribology,”
Evolution #4-2015, págs. 22-28.
[6] Morales-Espejel, G.E. y Gabelli, A. (2015), “The Progression of Surface Rolling Contact Fatigue Damage of Rolling Bearings with Artificial Dents,” Tribology Transactions, 58, págs. 418–431.
[7] Snare, B. (1970), “How Reliable Are Bearings?” The Ball Bearing Journal, 162, págs. 3–7.
[8] Morales-Espejel, G. E. y Brizmer, V. (2011), “Micropitting Modelling in Rolling–Sliding Contacts: Application to Rolling Bearings,” Tribology Transactions, 54, págs. 625–643.