Usura e fatica superficiale nei cuscinetti volventi
Anche dopo osservazioni, misurazioni e monitoraggi accurati è difficile prevedere e quantificare l’usura nei cuscinetti. SKF ha svolto molte ricerche e analisi dedicate allo studio dello strisciamento e dell’usura e al loro effetto sulla durata dei cuscinetti.
In alcune applicazioni i cuscinetti volventi possono subire perdite sostanziali di materiale (usura) per mancanza di lubrificazione, presenza di particelle abrasive, corrosione, rotazione oscillante e altre cause. Tale usura a sua volta può avere un effetto negativo sul funzionamento dei cuscinetti, dalla riduzione del precarico a effetti potenzialmente disastrosi. Una conseguenza comune e forse inaspettata dell’usura irregolare nelle piste dei cuscinetti è il possibile aumento della fatica superficiale. In alcune applicazioni non è insolito notare bande di fatica superficiale o sfaldature superficiali lungo le piste. Ciò è associato alla possibilità che il profilo della pista venga modificato dall’usura irregolare, che può dare origine a una concentrazione delle sollecitazioni nelle aree di carico maggiore e alla riduzione dello spessore del film di lubrificante che evita lo strisciamento dei corpi volventi.
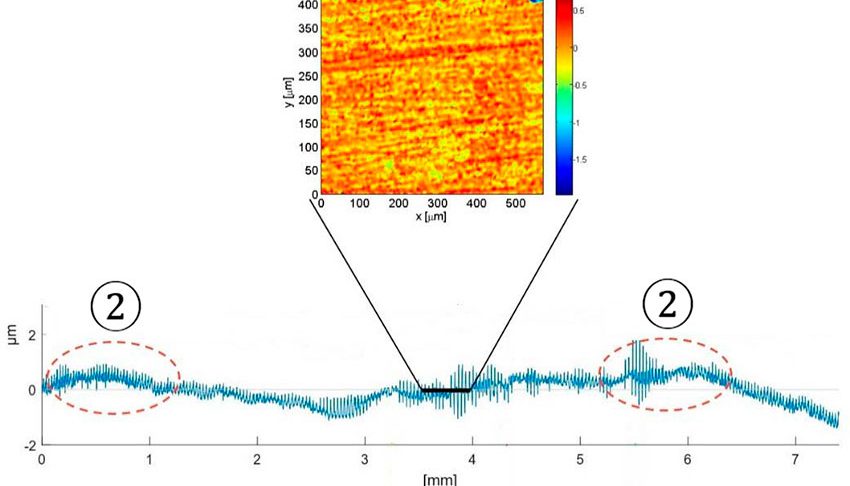
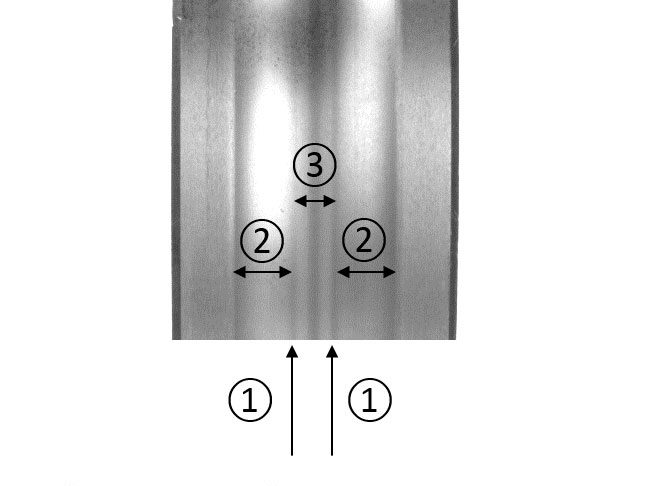
I cuscinetti volventi che funzionano in condizioni di scarsa lubrificazione in situazioni di strisciamento irregolare o in presenza di particelle abrasive o contaminazione di liquidi possono subire modifiche sostanziali nei profili delle piste (fig. 1). Nel tempo tali modifiche possono creare concentrazioni di sollecitazioni nelle zone di maggior carico (fig. 2) con un probabile aumento della fatica superficiale localizzata, producendo bande di fatica superficiale o sfaldature lungo le piste nelle aree maggiormente sollecitate (fig. 3). Questa modalità di danneggiamento potenziale può interessare qualsiasi applicazione che utilizza cuscinetti volventi, ma le più colpite sono le applicazioni con presenza di alta contaminazione, di sostanze corrosive, di scarsa lubrificazione e strisciamento irregolare o carico variabile. Alcuni esempi si ritrovano nell’industria mineraria, nel cartario, nelle applicazioni eoliche.
L’usura nei cuscinetti è un fenomeno non lineare e risulta difficile prevedere come evolverà nel tempo anche con osservazioni e misurazioni eseguite a intervalli regolari. Le ragioni di ciò sono varie; l’usura dipende principalmente dallo strisciamento e dal carico locale e lo stesso fenomeno dell’usura influisce a sua volta su questi due fattori, pertanto una semplice estrapolazione non è possibile. È necessaria un’analisi più rigorosa; ecco perché SKF si è impegnata molto nello studiare il fenomeno dello strisciamento e dell’usura nei cuscinetti e del loro effetto sulla durata [1].
Qualsiasi cuscinetto volvente ha un certo grado di strisciamento; questo è normale. È prodotto dalla geometria interna del cuscinetto e/o dalle condizioni di carico. Ad esempio, un cuscinetto a sfere o a rulli conici, caricato radialmente in modo corretto, avrà anche uno strisciamento (Heathcote slip) dovuto alla geometria di contatto tra anello e corpo volvente e una deformazione elastica dovuta al carico (figure 4a e 4b). Poiché l’usura dipende dallo strisciamento, con l’avanzare del funzionamento (se le condizioni vengono definite in modo corretto) si può prevedere che le bande di rotolamento (A e A1) saranno le uniche zone in cui non vi sarà usura e quindi le uniche zone a sopportare tutto il carico nel contatto.
Fortunatamente, un probabile danneggiamento si può verificare solo in situazioni di forte usura, come in presenza di particelle abrasive, corrosione importante o strisciamento anomalo dovuto a montaggio o carico inappropriato del cuscinetto. Nella maggior parte dei casi i cuscinetti funzionano in modo corretto e lo strisciamento sarà la normale condizione di lavoro di un cuscinetto senza creare problemi.
Il presente studio analizzerà un po’ più a fondo i meccanismi principali della modalità di danneggiamento con possibile combinazione di usura e fatica. Sono stati elaborati modelli e condotti esperimenti per comprendere meglio questo fenomeno e chiarire come prevenirlo.
Modellazione
Modellazione dell’usura
In [2] sono descritti diversi modelli di usura con la presenza di lubrificante e si è concluso che tutti i casi possono essere rappresentati con un modello di Archard [3], talvolta con un modello sofisticato utilizzando un coefficiente di usura. Nella maggior parte dei casi il coefficiente di usura è un fattore empirico basato su esperimenti. Pertanto, l’equazione di usura è:
Dove:
V = volume di usura [m3] in un intervallo di tempo,
![]() = coefficiente di usura di Archard adimensionale [-],
= coefficiente di usura di Archard adimensionale [-],
F = forza di contatto [N],
H = durezza del materiale superficiale corrente [Pa],
s = distanza di strisciamento [m] in un certo tempo.
Il volume di usura può essere espresso come:
Dove:
h = spessore dello strato superficiale rimosso [m] in un certo tempo,
As = area di strisciamento [m2] in un intervallo di tempo.
Pertanto, sostituendo (2) in (1) e considerando che la pressione di contatto media è ![]() :
:
Ora, considerando il tempo di contatto totale ![]() per ciclo di carico, che rappresenta il tempo di passaggio di entrambe le superfici di strisciamento attraverso l’area di contatto con la velocità di rotolamento, l’area di strisciamento è semplicemente l’area di contatto, pertanto As = A. Lo spessore dello strato rimosso per numero di rotolamenti (N) può essere calcolato seguendo [2] come:
per ciclo di carico, che rappresenta il tempo di passaggio di entrambe le superfici di strisciamento attraverso l’area di contatto con la velocità di rotolamento, l’area di strisciamento è semplicemente l’area di contatto, pertanto As = A. Lo spessore dello strato rimosso per numero di rotolamenti (N) può essere calcolato seguendo [2] come:
Dove:
us = velocità di strisciamento locale [m/s],
u1 = velocità media della superficie analizzata [m/s],
l = lunghezza di contatto lungo la direzione di strisciamento [m].
Si noti che quasi tutte le quantità sono su riferimenti (x,y.) locali. La durezza dell’acciaio delle piste e dei corpi volventi viene assunta come costante. Dall’equazione (4) si ottiene lo spessore locale dello strato usurato rimosso a ogni rotolamento dovuto al contatto del corpo volvente con la pista.
Modellazione dell’interazione fra usura e fatica
Per modellare l’interazione fra usura e fatica nei cuscinetti, occorre applicare un modello di fatica da contatto di rotolamento a ogni rotolamento della pista con un profilo modificato in precedenza (su entrambe le superfici) a causa dell’usura; in questo modo entrambi i fenomeni (usura e fatica) interagiscono. Ogni volta che l’usura modifica il profilo, per il modello di fatica occorre calcolare una nuova distribuzione della pressione nel contatto. Questo processo riflette ciò che accade nella realtà. Tuttavia il modello è molto dispendioso computazionalmente, considerato che la durata tipica della fatica da contatto di rotolamento può coprire milioni di rotolamenti. Pertanto vi sono semplificazioni che riducono sostanzialmente il carico computazionale:
- Si applica il calcolo di un contatto secco anziché una condizione di lubrificazione elastoidrodinamica (EHL) completa, considerando semplicemente un coefficiente di attrito fisso (misurato).
- Si aggiorna il profilo risultante dall’usura a intervalli di rotolamenti regolari, invece di eseguire l’aggiornamento a ogni singolo rotolamento.
- Il punto (2) ha inoltre come conseguenza che l’aggiornamento del calcolo del contatto e quello del danneggiamento (fatica) possono essere eseguiti anche contestualmente all’aggiornamento del profilo in seguito all’usura, invece che a ogni singolo rotolamento.
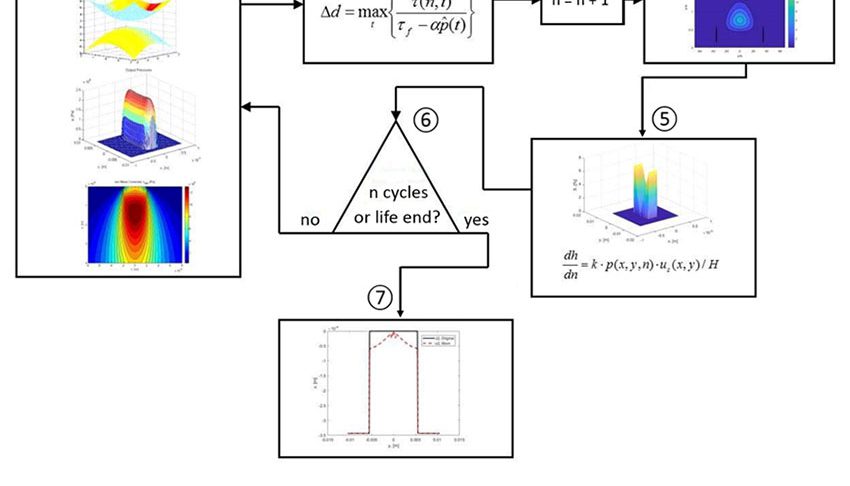
Il diagramma di flusso in figura 5 mostra un riepilogo della procedura di calcolo. Si noti che in questo caso si utilizza il criterio di fatica di Dang Van [4] e che il calcolo del danneggiamento viene effettuato mediante la legge lineare di Palmgren-Miner [5,6]. Tuttavia, si potrebbe utilizzare qualsiasi altro criterio di fatica e danno cumulativo, qualora gli esperimenti lo suggeriscano.
Esperimenti
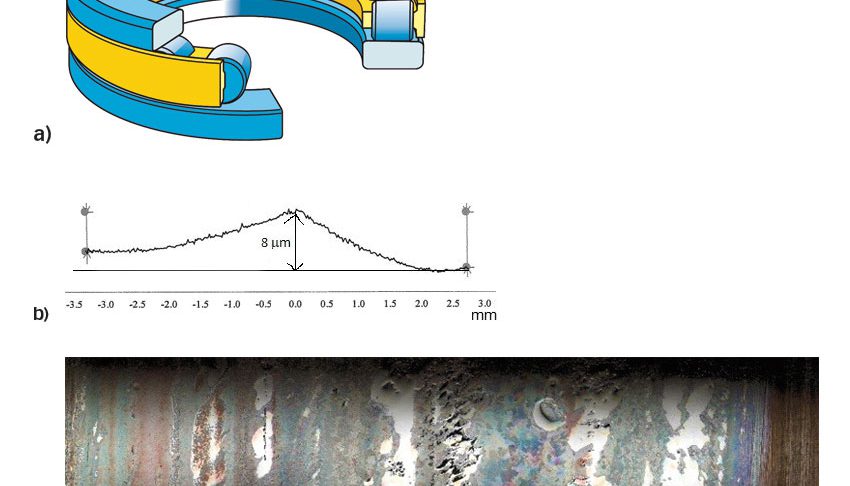
Per convalidare il modello di fatica, è stata condotta una prova di durata utilizzando un cuscinetto assiale a rulli cilindrici 81107 TN (fig. 6a), caricato assialmente con C/P = 6,5 e con rapporto di viscosità pari a ![]() ≈ 0.5.
≈ 0.5.
Prima di eseguire la prova, nei nuovi cuscinetti è stato realizzato un profilo artificiale (fig. 6b), come se i cuscinetti fossero stati sottoposti a condizioni di forte usura. Durante le prove alcuni cuscinetti si sono danneggiati, principalmente a causa di danneggiamenti ai rulli (fig. 6c), pertanto è stato possibile confrontare il modello di durata con i risultati della prova rapida. Nel modello in figura 5 sono stati considerati gli stessi rulli usurati e nuovi anelli; i risultati mostrano una buona concordanza con il limite inferiore della durata L10 misurata, considerando le statistiche di Weibull.
In parallelo sono stati eseguiti test e misurazioni dello stato di usura sul cuscinetto, per calcolare il coefficiente di usura e convalidare quindi il modello utilizzando diverse tipologie di esperimenti. Anche la concordanza tra modello ed esperimenti è stata soddisfacente.
Risultati
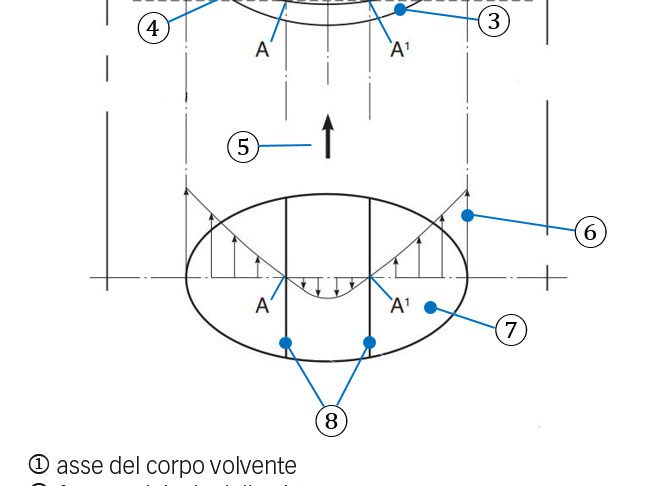
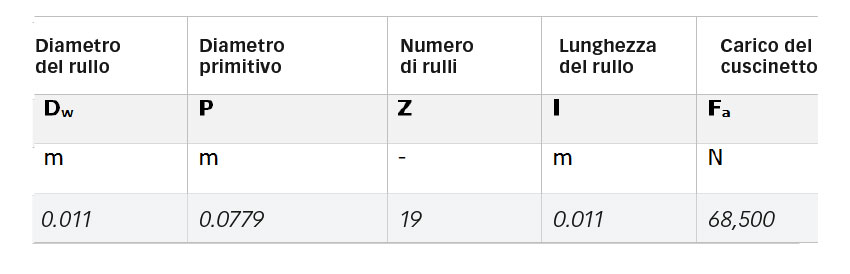
Nei cuscinetti assiali a rulli cilindrici lo strisciamento varia in modo lineare (diminuisce) dai due bordi dei rulli verso la circonferenza primitiva, dove lo strisciamento è pari a zero (fig. 7). Verso il diametro esterno del cuscinetto il rullo percorrerà la superficie più velocemente, mentre verso il diametro interno avanzerà più lentamente. Per illustrare gli effetti concomitanti di usura e fatica in un cuscinetto a rulli con strisciamento variabile lungo la pista, si è considerato un altro caso di un cuscinetto assiale a rulli di dimensioni maggiori (81212 TN), come indicato nei dati della Tabella 1.
È stata avviata una simulazione che consente al modello di modificare il profilo risultante dall’usura con un coefficiente di usura dimensionale (definito come ![]() ) con le condizioni di carico indicate nella Tabella 1 con una simulazione in grado di raggiungere nominalmente 300 milioni di rotolamenti.
) con le condizioni di carico indicate nella Tabella 1 con una simulazione in grado di raggiungere nominalmente 300 milioni di rotolamenti.
Invece di aggiornare i profili di usura a ogni rotolamento, per risparmiare tempo computazionale senza perdere accuratezza, è emerso che gli aggiornamenti potevano essere eseguiti ogni 15,5 milioni di rotolamenti sul rullo. Per la simulazione è stato applicato lo stesso modello rappresentato in figura 5, incluso il modello di usura di Archard di equazione (4).
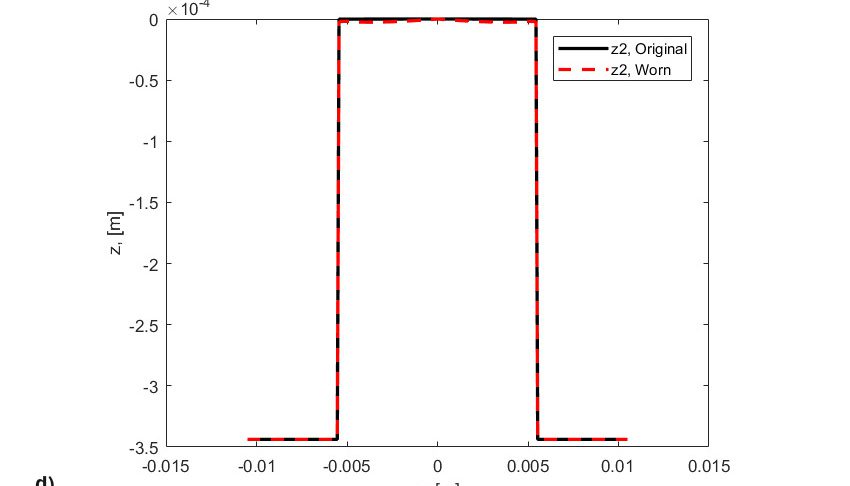
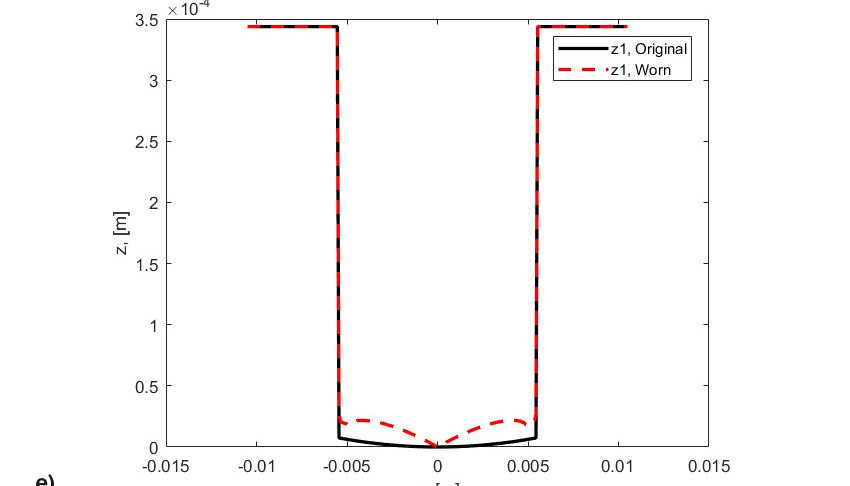
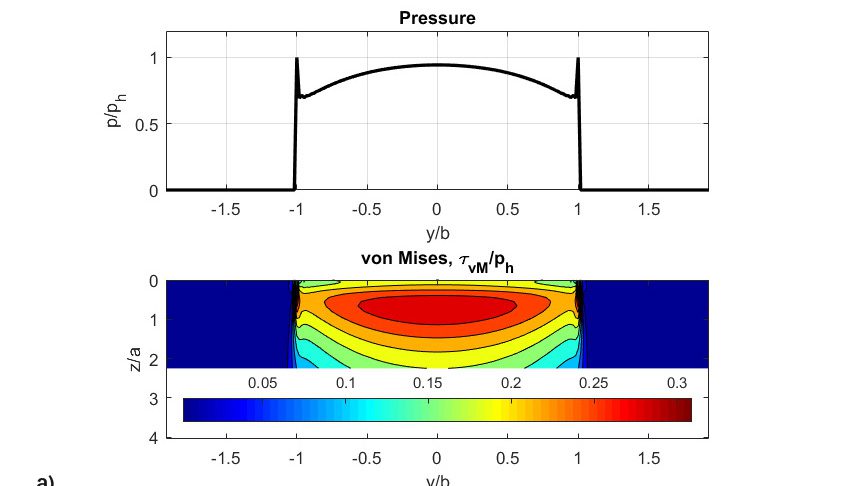
I risultati della simulazione sono mostrati in figura 8. La figura mostra:
- le pressioni adimensionali,
- le sollecitazioni di taglio di Von Mises,
- la mappa dei danneggiamenti,
- i profili originali di rulli e anelli,
- i profili usurati di rulli e anelli, corrispondenti alla fase temporale della fine delle simulazioni.
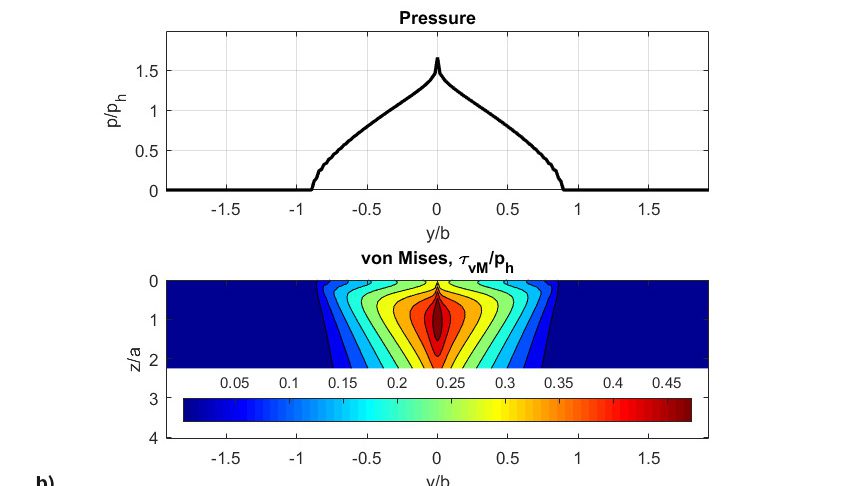
Occorre segnalare che la mappa dei danneggiamenti ha raggiunto un valore di danneggiamento totale superiore a 1 (soglia di innesco della cricca) dopo soli 31 milioni di rotolamenti. I risultati mostrati in figura 8 si riferiscono alle fasi iniziali e finali delle simulazioni. La pressione iniziale (fig. 8a) nel primo rotolamento sembra quasi hertziana, ma mostra un certo effetto di sollecitazione sui bordi, perché è stato utilizzato un profilo del rullo cilindrico semplice, invece di un rullo opportunamente profilato che avrebbe evitato tali sollecitazioni sui bordi. Dai risultati si evince che lo strisciamento è pari a zero nella circonferenza primitiva; inoltre la parte del modello di usura di Archard della simulazione indica che non vi è usura in quel punto.
Sicuramente l’usura è collegata alla distribuzione dello slittamento lungo la pista. Pertanto, l’usura si verifica con maggiore frequenza spostandosi dalla circonferenza primitiva della pista. Si noti che in origine la pressione di contatto era quasi rettangolare (fig. 8a), ma, poiché è stato rimosso del materiale dai due lati del contatto di rotolamento, la pressione è ridotta nelle aree con scorrimento elevato ed è fortemente aumentata e concentrata nell’area con strisciamento pari a zero (circonferenza primitiva), (fig. 8b). Tale pressione aumentata produce forti sollecitazioni, innescando il fenomeno della fatica più velocemente, finché non si sviluppa un cedimento al centro del rullo (fig. 8c). L’effetto simultaneo e concomitante di usura e fatica può sicuramente accelerare la sfaldatura da fatica da contatto di rotolamento. Questa sfaldatura da fatica accelerata non è correlata alla sollecitazione di attrito indotta dallo strisciamento, ma è piuttosto il risultato della modifica del profilo originale dei corpi volventi (figure 8d e 8e), che porta a un notevole aumento delle sollecitazioni interne e a un ridotto spessore localizzato del film di lubrificante.
Conclusioni
Dalla modellazione degli effetti concomitanti di usura abrasiva e fatica da contatto di rotolamento, si evince che lo strisciamento può diventare un elemento importante per l’aumento dei danneggiamenti da fatica di un cuscinetto. Ciò richiede la presenza di particelle abrasive e/o condizioni di lubrificazione scarse nel cuscinetto. Anche una distribuzione non uniforme dello slittamento nel contatto hertziano contribuisce a un aumento delle sollecitazioni interne, che riducono notevolmente l’aspettativa di durata a fatica del cuscinetto. Sicuramente questo sembra essere il meccanismo più significativo con cui lo strisciamento hertziano potrebbe ridurre la durata a fatica da contatto di rotolamento del cuscinetto.
Per ridurre questo rischio, sono riportate di seguito alcune raccomandazioni:
- Assicurarsi che il cuscinetto sia sempre lubrificato in modo adeguato, in particolare nel caso di cuscinetti di grandi dimensioni con bassa velocità di rotazione o con oscillazione, cuscinetti in presenza di grandi quantità di particelle abrasive o esposti a sostanze corrosive.
- Ottimizzare le soluzioni di tenuta utilizzando cuscinetti muniti di tenute/schermi.
- Ridurre quanto più possibile la contaminazione da solidi.
- Evitare vibrazioni e carichi d’urto che possano aumentare notevolmente le condizioni di strisciamento nominali del cuscinetto.
- Nel caso di cuscinetti di grandi dimensioni, se si rileva per tempo l’usura irregolare, il ricondizionamento può essere un aspetto da prendere in considerazione.
Autori:
Guillermo E Morales-Espejel,
Guillermo E. Morales-Espejel, scienziato principale, SKF Research & Technology Development, Nieuwegein, Paesi Bassi
L’autore desidera ringraziare Ralph Meeuwenoord per il supporto dato nella fase sperimentale di questo progetto.
Bibliografia
[1] Morales-Espejel, G.E., Gabelli, A., Rolling Bearing Seizure and Sliding Effects on Fatigue Life, Proc. IMechE, part J, Journal of Eng. Tribology, DOI: 10.1177/1350650118779174, 2018.
[2] Morales-Espejel, G.E., Brizmer, V., Piras, E., Roughness Evolution in Mixed Lubrication Condition due to Mild Wear, Proc. IMechE, part J, Journal of Eng. Tribology, 229(11), pp. 1330-1346, 2015.
[3] Archard, J.F., Contact and Rubbing of Flat Surface, Journal of Applied Physics; 24(8): 981–988, 1953.
[4] Dang Van, K., Griveau, B., and Message, O., On a New Multiaxial Fatigue Limit Criterion: Theory and Application, Biaxial and Multiaxial Fatigue, Brown, M. and Miller, K. (Eds.), Mechanical Engineering Publications: London, pp. 479-498, 1989.
[5] Palmgren, A., Die Lebensdauer von Kugellagern [Life Length of Roller Bearings], Zeitschrift des Vereines Deutscher Ingenieure (VDI Zeitschrift), 68(14), 1924,
pp 339-341. (In German)
[6] Miner, M.A., Cumulative Damage in Fatigue, Journal of Applied Mechanics, 67 A157, 1945.








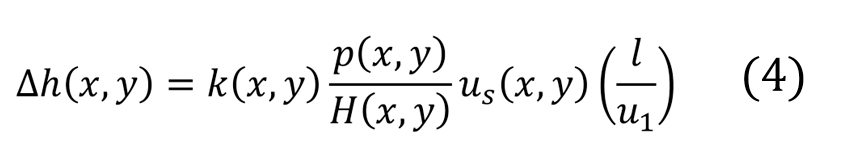

![Fig. 8: c) mappa dei danneggiamenti di Palmgren-Miner dopo la simulazione per lo stesso esempio della Tabella 1 con un coefficiente di usura di Fig. 8: c) mappa dei danneggiamenti di Palmgren-Miner dopo la simulazione per lo stesso esempio della Tabella 1 con un coefficiente di usura di =0.5x10-11 [s]](https://evolution.skf.com/wp-content/uploads/sites/5/2019/06/wear-and-surface-fatigue-in-rolling-bearings-fig8c-1-850x486.jpg)