滚动轴承磨损
和表面疲劳
即使借助仔细的观察、测量和监测,滚动轴承内发生的磨损也难以实现精确地预测。SKF在滑动和磨损以及它们对轴承寿命的影响等方面做了大量的研究和分析工作。
在一些应用场合中,滚动轴承由于缺乏润滑、存在污染颗粒、腐蚀、摆动运行等原因会造成其材料的大量损失(磨损)。而磨损反过来又会对轴承的运行产生不利影响,导致预紧力减少,甚至可能会引发灾难性的后果。轴承滚道上发生不均匀磨损会造成一种常见且出人意料的后果:使轴承出现表面疲劳的可能性大大增加。
在另外一些应用场合中,如果沿轴承滚道方向上普遍出现带状的表面劣化或表面剥落的情况,这可能与不均匀磨损导致轴承滚道轮廓发生变形相关。这会造成轴承内部产生应力集中和润滑油膜厚度降低。
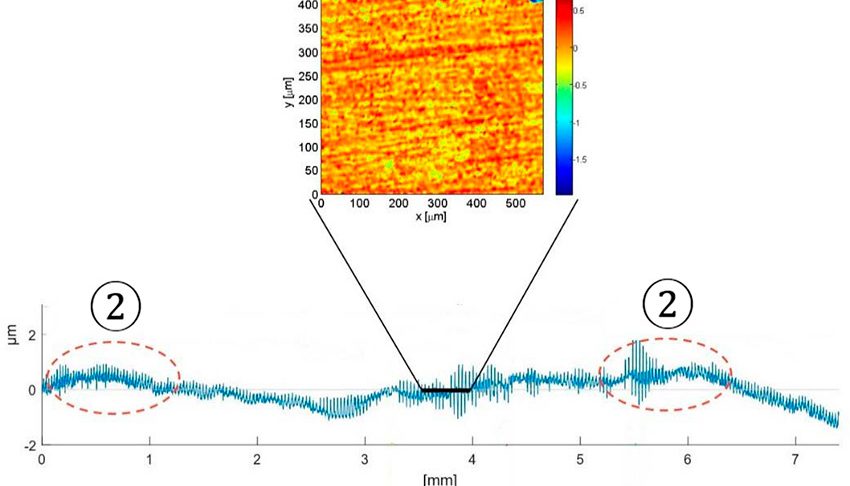
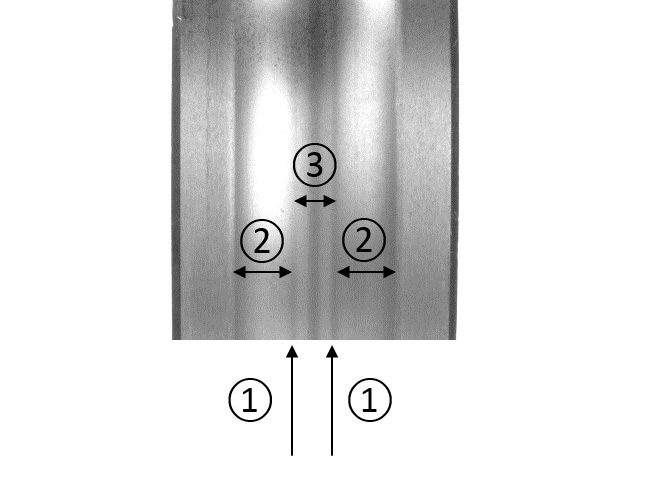
滚动轴承在润滑不良的条件下运行、或运行时出现不均匀滑动、或润滑剂中有磨粒磨损的颗粒、或有液体污染存在时,滚道的轮廓形貌可能会发生大幅改变(图1)。随着时间的推移,伴随轴承滚道上的形貌变化的发展,会导致大多数的承载区出现应力集中(图2)的现象,这可能会有局部区域出现表面疲劳的情况增加,表现为轴承滚道的高应力区内出现微点蚀带或剥落带(图3)。任何类型的滚动轴承都有可能受到这种损伤模式的影响,但是这种损伤模式在有严重污染、腐蚀、润滑不良以及存在不均匀滑动或变化载荷的应用中的影响最为显著。在采矿业、纸浆和造纸行业、风能应用和其他行业的应用中可以找到这类失效模式的实例。
滚动轴承的磨损是一种非线性现象,即使定期观察和测量滚动轴承磨损,结果也表明仅凭直觉不足以预测磨损会如何随时间演变。造成这一状况有多种原因:磨损主要取决于局部滑动和局部载荷,而磨损本身会改变这两个因素,因此无法进行简单外推。需要进行更严格的分析,因此,SKF才在滚动轴承的滑动和磨损以及它们对轴承寿命的影响等方面做了大量研究工作[1]。
任何滚动轴承内部都会发生一定程度的滑动,出现滑动是一种正常现象,是由轴承内部的几何形状和/或载荷状态所造成的。例如,承受纯径向载荷的径向球轴承或滚子轴承内部也会有一定的滑动(Heathcote滑动)发生(图4a和4b),这是由于滚动体与轴承套圈接触的几何形状和在载荷作用下的弹性变形造成的。由于滑动会导致磨损产生,那就可以预期:随着时间推移(如果给定条件合适),纯滚动带(A和A1)将是唯一不会发生磨损的区域,会导致它在经过一段时间后成为接触面中唯一承载所有载荷的区域。
幸运的是,这种情况只会发生在严重磨损的情况下,例如存在磨粒磨损的颗粒、严重腐蚀、或由于轴承承受不恰当的载荷、或不正确的安装而导致的异常滑动。在大多数情况下,轴承正常工作时,这种滑动是滚动轴承在正常工作时的一种现象,不会导致问题的发生。
本文将对潜在的磨损-疲劳复合损伤模式的主要机理进行深入的探讨。为了更好地理解这类机理,并为预防这类损伤模式的方法提供一些思路,我们进行了相应的建模和试验。
建模
磨损建模
在文献[2]中,讨论了在不同润滑条件下的磨损模型,并且得出在所有情况下,它们可以用Archard模型[3]来表示,但有时需使用带有磨损系数的更为精密的模型。在大多数情况下,磨损系数是通过试验得到的经验系数。因此,最常见的磨损计算公式是:
其中:
V = 一定时间内的磨损量[m3],
![]() = Archard无量纲磨损系数[-],
= Archard无量纲磨损系数[-],
F = 接触压力[N],
H = 材料表面硬度[Pa],
s = 一定时间内滑动的距离[m]。
磨损量可以表示为:
其中:
h = 一定时间内去除的表面层厚度[m],
As = 一定时间内滑动的面积[m2]。
这样,将(2)代入(1),同时假定平均接触压力 :
现在,每个载荷循环的总接触时间 ![]() ,它表示两个滑动表面以滑动速度通过整个接触区域所花的时间,那么滑动面积就是接触面积,因此As = A。总滚动次数(N)中每次滚动时的去除层厚度可以通过以下[2]计算得出:
,它表示两个滑动表面以滑动速度通过整个接触区域所花的时间,那么滑动面积就是接触面积,因此As = A。总滚动次数(N)中每次滚动时的去除层厚度可以通过以下[2]计算得出:
其中:
us = 在某一位置时的滑动速度[m/s]
u1 = 分析表面的平均速度[m/s]
l = 沿着滑动方向的接触长度[m]。
注意几乎所有数量都是局部的(x,y)。此外,假设滚道和滚动体钢材的硬度保持不变。等式(4)给出了轴承接触面中每次滚动时某一位置去除的磨损层厚度。
磨损-疲劳之相互作用的建模
为了建立轴承磨损/疲劳相互作用的模型,需要在每次滚动碾压通过因磨损而导致表面形貌发生变化的滚道时,都应用滚动接触疲劳(RCF)模型对其进行研究,用这种方法让这两种现象(磨损和疲劳)发生相互作用。每次磨损改变其表面形貌时,就需要用疲劳模型计算接触面上新的压力分布情况。这一过程反应轴承的实际运行情况。然而,考虑到要获得典型滚动接触的疲劳寿命就需要数百万次滚动碾压通过后进行的计算,站在计算的角度上讲,其代价十分高昂。因此,我们对这种方法进行了简化,大幅降低了计算成本:
- 没有采用完全弹性流体动力润滑(EHL)条件,而是采用干接触条件的方法进行计算,这样就只需要简单考虑固定的摩擦系数(测量到的),从而避免了润滑带来的问题。
- 在经过一定次数的重复滚动碾压通过后再更新表面形貌,而不是在每次滚动碾压通过时都对其表面形貌进行更新。
- 如(2)这样的处理,就意味着:接触计算和损伤(疲劳)计算结果,可以实现在更新磨损的表面形貌时也同时进行了更新,而不是每次滚动碾压通过后就更新。
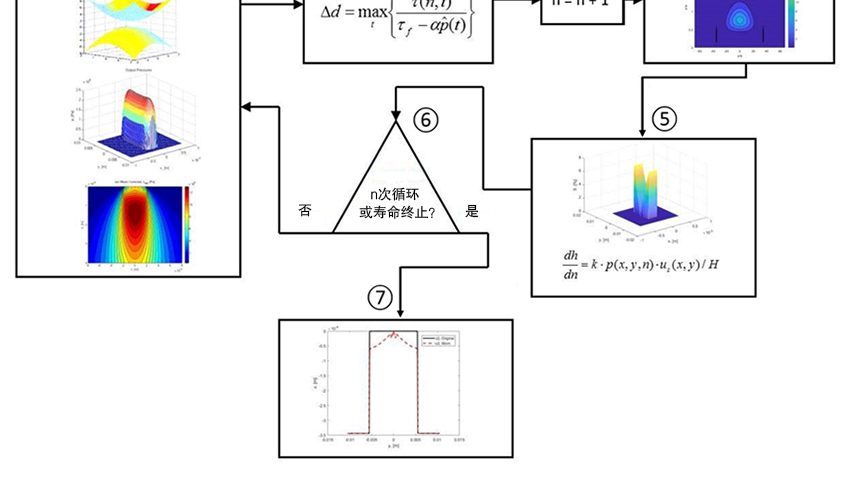
右侧的的图5流程图是这个计算过程的简要图。注意,此计算模型使用了Dang Van [4]疲劳准则,累积损伤是通过Palmgren-Miner线性准则[5, 6]来完成的。但如果试验需要,可以使用其他任何疲劳标准和累积载荷损伤。
试验
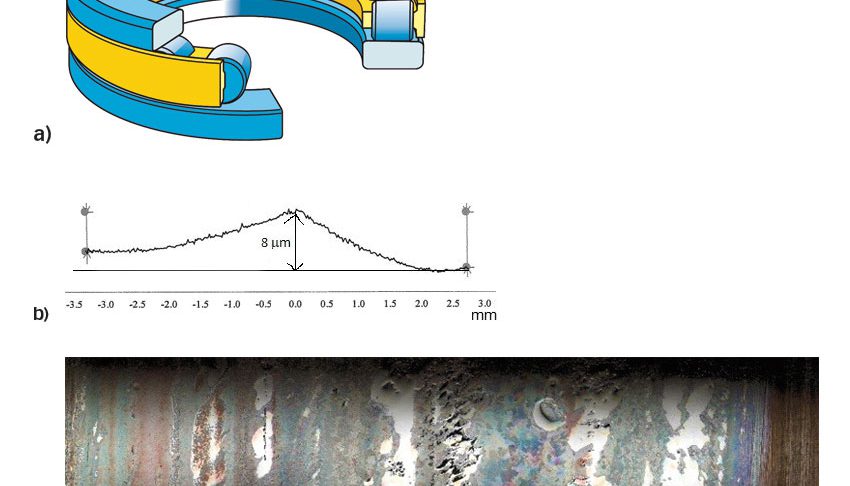
通过圆柱推力滚子轴承81107 TN(图6a)的耐久性试验来验证疲劳模型,轴向载荷C / P = 6.5,给出的润滑条件 ![]() ≈ 0.5。
≈ 0.5。
在试验之前,将新轴承的滚道加工成特殊的轮廓形貌(图6b),使它们就像在严重磨损条件下运行过一段时间一样。在试验过程中,部分轴承出现了失效,主要是滚子损坏(图6c)。因此,可以将寿命模型与这个短时间试验结果进行比较。在图5模型中的滚子和新座圈的磨损认为是完全相同的。考虑了Weibull统计后的结果显示与测量到的L10寿命的下限吻合得非常好。
同时,还对全部轴承的磨损情况进行了试验和测量,以计算磨损系数,然后不同试验组使用不同的验证模型。模型和试验结果也吻合得比较好。
结果
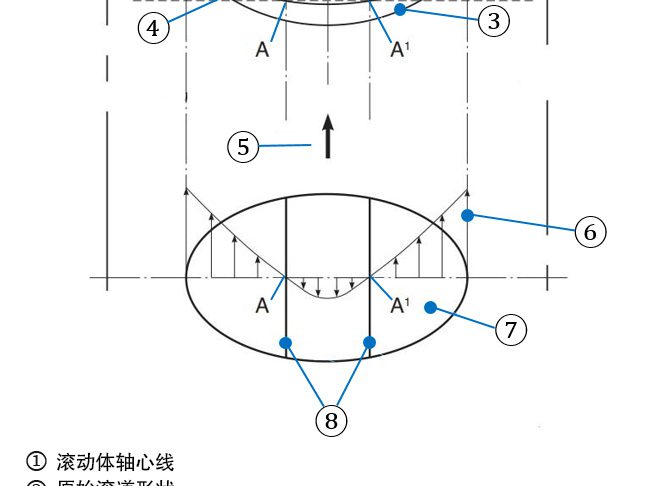
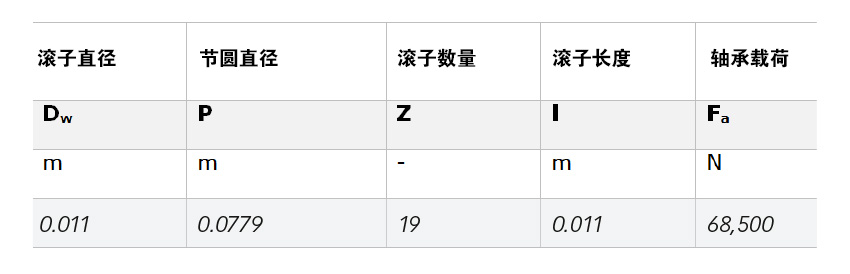
在推力圆柱滚子轴承中,滑动从滚子的两端向节圆线方向上出现线性变化(减小),节圆线处的滑动为零(图7)。越靠轴承外侧,滚子表面的速度越快;越靠轴承内侧,滚子表面的速度越慢。为了说明在滚道轴向上存在的变化滑动可以对滚动轴承的磨损和疲劳同时产生的影响,实验使用了另一个更大的轴承(81212 TN)进行试验,轴承(81212 TN)的数据列于表1中。
通过仿真模拟,该模型能够根据表1的载荷条件下产生的形貌磨损情况,通过引入一个无量纲的磨损系数,无量纲磨损系数(定义是![]() ),(进一步)对(滚道接触)形貌轮廓进行修正。该仿真模拟程序能够预测到(滚道)经过3亿次滚动碾压通过后的叠加结果。
),(进一步)对(滚道接触)形貌轮廓进行修正。该仿真模拟程序能够预测到(滚道)经过3亿次滚动碾压通过后的叠加结果。
研究发现可以在每经历1,550万次滚动碾压通过后进行一次滚道表面磨损轮廓形貌更新,就既节省计算时间,又不损失结果的精确性。此仿真采用图5中所示的模型,并包涵公式(4)的Archard磨损模型。
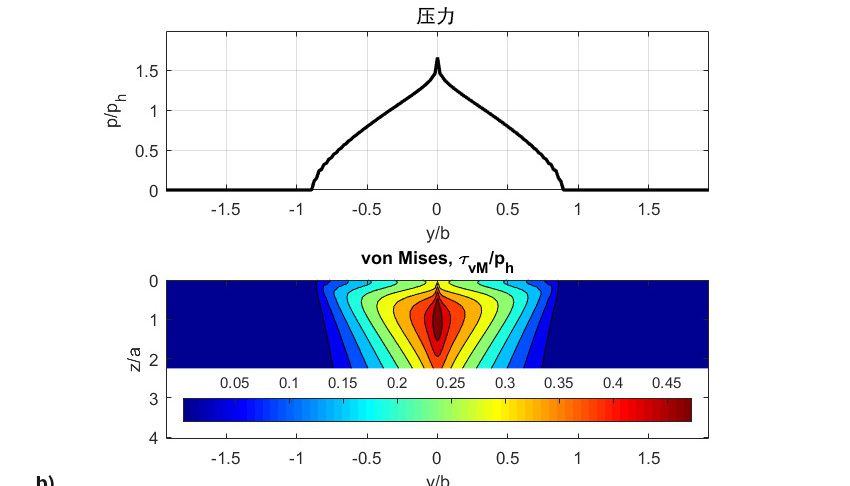
- 无量纲压力,
- von Mises剪切应力,
- 损伤图,
- 滚子和座圈原始的形貌轮廓,
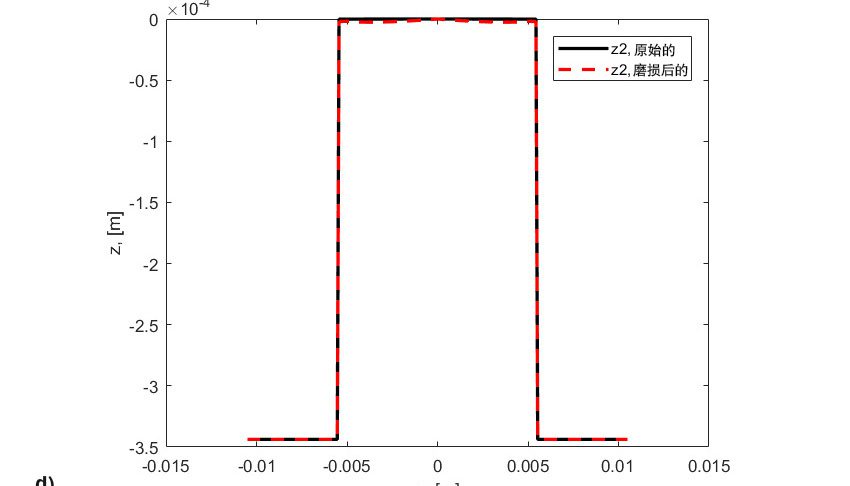
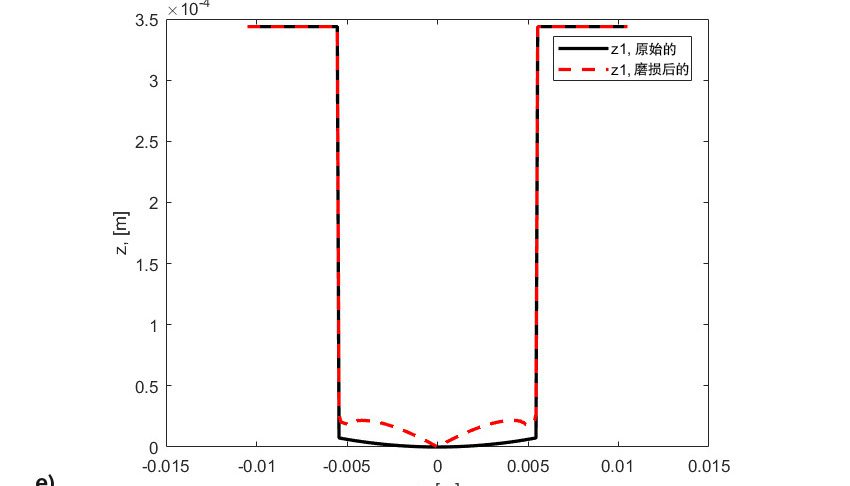
- 滚子和座圈磨损后的形貌轮廓,对应于仿真结束时的时间段。
必须指出的是,在仅有3,100万次滚动后,损伤图的总损伤值就超过了1(裂纹萌生阈值)。图8中的结果与初始和最终仿真步骤有关。第一次滚动碾压通过的初始压力(图8a)看上去有些像赫兹接触应力的曲线,但由于使用的是简单的直线轮廓滚子,而没有使用能够避免出现边缘应力的适合轮廓曲线的滚子,因此就显示出了边缘应力集中的效应。从结果可以看出,节圆线处的滑动为零。此外,仿真中的Archard磨损模型部分表明该位置的磨损为零。
实际上,磨损与滚道沿轴向的滑动分布有关。因此,离节圆线越远的滚道,磨损就越快。值得注意的是,初始的接触压力近乎是矩形分布(图8a),但随着滚动接触两侧的材料被磨损去除后,高滑动区域的压力减小,使得零滑动区域(节圆线)(图8b)处的压力大幅增加并产生应力集中。
这种压力导致滚子的中部产生高应力和发生疲劳的速度更快,直到其失效(图8c)。在同时发生的磨损和疲劳的共同影响下,它们的确可以使接触面的RCF剥落速度出现加速。这种加速疲劳剥落与滑动引起的摩擦应力无关,而是由于滚动体原始轮廓形貌的改变(图8d和8e)导致接触应力急剧上升和局部油膜厚度下降造成的。
结论
本文对磨粒磨损和滚动接触疲劳同时作用进行了建模,结果表明滑动可能成为轴承疲劳损伤增加的重要因素。轴承中存在磨损的颗粒和/或处于较差的润滑条件下常见。赫兹接触区内不均匀滑动分布也会成为应力发展增加的因素,这会显著缩短轴承预期的疲劳寿命。实际上,赫兹接触区内的滑动似乎也是最终缩短轴承滚动接触疲劳寿命(RCF)最重要的成因。
为降低这类风险,建议采用如下措施:
- 确保轴承始终有足够的润滑,特别是那些低速旋转或摆动运动的大型轴承,以及那些内部存在大量磨粒磨损的颗粒或暴露于腐蚀性环境的轴承。
- 优化密封解决方案,最终采用密封/防尘轴承。
- 尽可能减少固体和液体污染。
- 避免会显著增加轴承的标称滑动条件的冲击负荷和振动。
- 对于大型轴承,如果检测到不均匀磨损,从节约成本角度方面考虑,可以选择对轴承进行修复。
作者:
Guillermo E Morales-Espejel,
SKF研究和技术开发部(RTD)首席科学家,荷兰尼沃海恩
作者感谢Ralph Meeuwenoord在本项目试验阶段给予的热心支持。
参考文献
[1] Morales-Espejel, G.E., Gabelli, A., Rolling Bearing Seizure and Sliding Effects on Fatigue Life, Proc. IMechE, part J, Journal of Eng. Tribology, DOI: 10.1177/1350650118779174, 2018.
[2] Morales-Espejel, G.E., Brizmer, V., Piras, E., Roughness Evolution in Mixed Lubrication Condition due to Mild Wear, Proc. IMechE, part J, Journal of Eng. Tribology, 229(11), pp. 1330-1346, 2015.
[3] Archard, J.F., Contact and Rubbing of Flat Surface, Journal of Applied Physics; 24(8): 981–988, 1953.
[4] Dang Van, K., Griveau, B., and Message, O., On a New Multiaxial Fatigue Limit Criterion: Theory and Application, Biaxial and Multiaxial Fatigue, Brown, M. and Miller, K. (Eds.), Mechanical Engineering Publications: London, pp. 479-498, 1989.
[5] Palmgren, A., Die Lebensdauer von Kugellagern [Life Length of Roller Bearings], Zeitschrift des Vereines Deutscher Ingenieure (VDI Zeitschrift), 68(14), 1924,
pp 339-341. (In German)
[6] Miner, M.A., Cumulative Damage in Fatigue, Journal of Applied Mechanics, 67 A157, 1945.








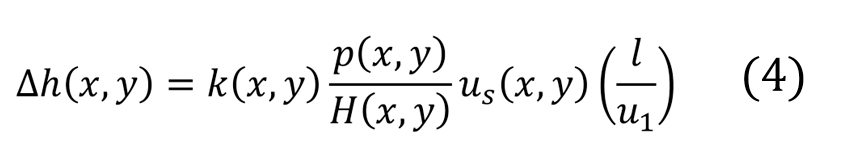


![图8:c) 以磨损系数 =0.5x10-11 [s] 对表1的相同例子进行仿真后的Palmgren-Miner损伤图 图8:c) 以磨损系数 =0.5x10-11 [s] 对表1的相同例子进行仿真后的Palmgren-Miner损伤图](https://evolution.skf.com/wp-content/uploads/sites/5/2019/06/wear-and-surface-fatigue-in-rolling-bearings-fig8c-ch-850x486.jpg)