La fatica da contatto di rotolamento (Rolling Contact Fatigue, RCF) è un danneggiamento tipico dei cuscinetti volventi e di altri componenti delle macchine. Lundberg e Palgren avevano svolto in proposito un lavoro fondamentale [1], [2]. La teoria da loro elaborata era essenzialmente concentrata sulla fatica sotto la superficie del contatto e si basava interamente su calcoli delle sollecitazioni hertziane con superfici teoriche ideali. La fatica superficiale da contatto di rotolamento (Surface Rolling Contact Fatigue, SRCF) si riferisce invece alla zona prossima alla superficie del contatto (ad una profondità di alcuni micron) che è fortemente influenzata dalle trazioni locali di superficie e dalle sollecitazioni legate alle caratteristiche geometriche della superficie stessa, come la rugosità, le variazioni di profilo, le eventuali impronte, ecc. L’interazione tra il film lubrificante elastoidrodinamico (EHL) e le caratteristiche che danno luogo alle suddette sollecitazioni in superficie è molto importante per comprendere i fenomeni di fatica superficiale nei cuscinetti volventi (Morales-Espejel e Gabelli [3]). Nel presente articolo si indaga sul modo nel quale la fatica superficiale da contatto SRCF progredisce, modellando il contatto e l’interazione con le variazioni della micro-geometria superficiale che generano concentrazioni di sollecitazioni. Il confronto tra le simulazioni numeriche e un insieme di risultati sperimentali mostra una buona correlazione, permettendo di formulare un’ipotesi sui meccanismi di base della SRCF, come pure sul suo inizio e progresso nei cuscinetti volventi. Queste nuove conoscenze aderiscono molto bene all’idea di base del modello generalizzato di durata SKF (SKF Generalized Bearing Life Model, GBLM), che tratta separatamente il danno a fatica della superficie da quello sotto-superficiale del contatto [4] [5].

Indagini teoriche sulla progressione del danno a fatica
Spesso, il danno a fatica da contatto di rotolamento si crea attorno a particolarità micro-geometriche della superficie e porta alla formazione di una cricca. La propagazione della cricca, nella sua forma più avanzata, è fortemente influenzata dalle modificazioni della macro-geometria – per esempio, l’evoluzione della geometria del contatto nella pista di rotolamento e il conseguente campo globale delle sollecitazioni del cuscinetto. Molti ricercatori hanno studiato la propagazione della cricca a fatica nei cuscinetti volventi, nel tentativo di collegare tra di loro i vari aspetti meccanici che controllano la progressione del danno a fatica. In una recente indagine, servendosi sia di modelli sia di esperimenti, gli autori del presente articolo [6] hanno studiato la propagazione della fatica SRCF sulle piste di cuscinetti su cui erano state praticate delle impronte. Fu trovato che i meccanismi di fatica richiedono di tener conto delle condizioni di lubrificazione del cuscinetto e dell’interazione delle sollecitazioni tra la superficie e la zona sotto la superficie del contatto. Questo per capire come si sviluppano le tipiche cricche a forma di V presenti lungo le piste di cuscinetti a sfere, a differenza della crescita trasversale del danno iniziale che si osserva nei cuscinetti a rulli e che può essere sufficientemente spiegato assumendo nei calcoli, semplici condizioni di contatto a secco.

Osservazioni sperimentali della progressione del danno
Nella sua analisi statistica sull’affidabilità dei cuscinetti, Snare [7] aveva monitorato la propagazione di una scheggiatura a fatica in un cuscinetto a rulli cilindrici e poté chiaramente notare come il danneggiamento progredisca trasversalmente alla pista prima di iniziare a propagarsi lungo la stessa. La fig. 1 illustra i test da lui eseguiti.

Le attuali conoscenze
Dalle indagini teoriche e sperimentali descritte nella letteratura, si possono chiaramente osservare almeno due fasi distinte della propagazione delle cricche o scheggiature da difetti superficiali. La prima si ha quando la scheggiatura cresce attraverso la pista più o meno lentamente e la seconda quando cresce lungo la pista di rotolamento in modo accelerato. Il fatto che inizialmente la scheggiatura si propaghi in senso trasversale è una diretta conseguenza delle sollecitazioni presenti sui suoi bordi diametrali, lungo la direzione ortogonale al rotolamento, che sono maggiori rispetto a quelle presenti sul bordo anteriore e su quello posteriore dell’impronta in direzione del rotolamento.

La formazione e propagazione del danno a fatica si differenzia chiaramente nel caso dei cuscinetti a sfere (fig. 2) e di quelli a rulli (fig. 3). Nei primi le cricche di superficie hanno inizio nel bordo posteriore dell’impronta e assumono subito la caratteristica forma a V, crescendo rapidamente nella direzione di rotolamento con distacco progressivo di materiale dalla zona danneggiata a forma di V. La crescita della zona scheggiata avviene nella direzione del rotolamento, che è il verso opposto alla direzione dell’attrito superficiale e dello strisciamento presente in quel punto (fig. 2). Nei cuscinetti a rulli le scheggiature che si formano in superficie si propagano inizialmente sui due lati dell’impronta, per poi crescere trasversalmente alla pista prima di espandersi lungo quest’ultima (fig. 3).

L’obiettivo del presente articolo è di comprendere meglio l’evoluzione del danno a fatica, con innesco superficiale, nei cuscinetti a rulli. Inoltre si vuole ampliare la conoscenza, tramite modelli, dei meccanismi che controllano la propagazione del danno che è osservato negli esperimenti. Questo fa seguito al lavoro, riportato dagli autori in [3], sui meccanismi dell’insorgere del danno superficiale che viene ora esteso allo studio dettagliato della fase di propagazione dell’area danneggiata.

Lavoro sperimentale
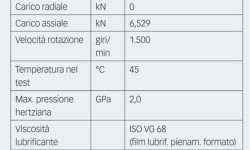
Sono stati condotti esperimenti sui cuscinetti a rulli conici standard, ved. tabella 1.

I cuscinetti sono stati artificialmente danneggiati mediante una sfera di carburo di tungsteno di 1 mm di diametro e un carico di 1.250 N, in grado di produrre impronte di 400 µm di diametro e 30 µm di profondità e con bordi a rilievo di circa 2 µm. L’esperimento prevedeva la creazione di otto impronte equidistanti attorno alla pista dell’anello interno, disponendole sfalsate in senso trasversale a 0,5 mm una dall’altra, partendo dal bordo della pista. Tuttavia, in questo articolo viene discussa nel dettaglio solamente l’evoluzione del danneggiamento delle impronte situate al centro della pista. Nelle condizioni di lavoro indicate in tabella 1, il carico assiale dava luogo ad una impronta hertziana larga circa 142 µm in direzione del rotolamento, sostanzialmente più stretta rispetto al diametro dell’impronta. Gli sperimenti sono stati eseguiti con numeri di giri diversi osservando l’evoluzione della fatica, risultante dalla concentrazione delle sollecitazioni e dalle condizioni di lubrificazione delle impronte.

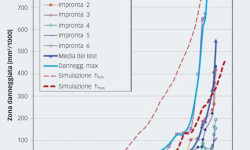
La fig. 4 illustra il risultato di alcuni esperimenti sull’evoluzione delle scheggiature su cuscinetti a rulli conici con l’aumento del numero di giri. La scheggiatura inizia da un lato dell’impronta e poi progredisce a entrambi i lati attraverso la pista, ossia in direzione perpendicolare al rotolamento. Nella fig. 4(b) è riportato un ellisse di contatto approssimativo per confronto con lo stadio finale della scheggiatura. Per rilevare le fasi di innesco e propagazione delle scheggiature sono stati monitorati molti anelli interni con ispezioni periodiche al microscopio ogni 5 milioni di giri. Tutte le impronte sono state ispezionate al microscopio e fotografate, eseguendo misurazioni sulle immagini digitali ottenute. I risultati di questo lavoro hanno fornito informazioni molto precise sull’innesco e la successiva crescita della zona scheggiata in funzione del numero di giri. I dati acquisiti sulle sei impronte che hanno dato origine a scheggiature sono illustrati in fig. 5.

Un’ispezione più particolareggiata della media dei dati dei test rivela che l’evoluzione dell’area scheggiata avviene in tre fasi:

1. un periodo di incubazione pari a 50-60 milioni di giri, in cui sulla pista non si nota alcun danneggiamento; questo corrisponde a circa la durata di base del cuscinetto.
2. una fase iniziale di danneggiamento, che si estende per 30-40 milioni di giri e, come prevedibile, mostra una crescita esponenziale dell’area danneggiata.
3. una crescita accelerata, che si estende per 20-25 milioni di giri, durante la quale il ritmo di crescita aumenta sensibilmente (più del doppio rispetto al periodo precedente).

Modello di propagazione del danneggiamento
Il calcolo del danneggiamento nel contatto di rotolamento si effettua modellando in primo luogo l’impronta iniziale sulla pista, mediante una funzione analitica parametrica che ne riproduce fedelmente la forma.

La geometria dell’impronta è quindi inclusa in un modello di contatto di rotolamento che riproduce la sollecitazione ciclica hertziana del cuscinetto in esame. Il calcolo del danneggiamento progressivo viene eseguito utilizzando il modello base della fatica superficiale e del distacco precedentemente elaborato da Morales-Espejel e Brizmer [8] e qui descritto, ma con alcune modifiche e adattamenti. Per esempio, la procedura di calcolo dell’usura, descritta in [8], è stata esclusa per accelerare le simulazioni. Nelle situazioni in cui l’impronta iniziale è più ampia del contatto hertziano nella direzione di rotolamento (come nel caso della simulazione dei cuscinetti a rulli conici di 4a) è stato escluso anche il modello della lubrificazione veloce, utilizzando solo quello del contatto a secco. Il modello viene poi utilizzato nel calcolo delle pressioni e delle sollecitazioni complessive. L’approssimazione è ritenuta valida in quanto in questo caso è probabile che il lubrificante sfugga dall’impronta e dal contatto. Non è prevedibile alcuna pressione elastoidrodinamica sui bordi dell’impronta, le cui pressioni si possono quindi modellare utilizzando l’ipotesi del contatto a secco (nel caso dei cuscinetti a sfere con una zona di contatto hertziana più ampia il modello con lubrificazione non può essere ignorato).

Una volta calcolate le pressioni di contatto, si ricava la storia delle sollecitazioni per una serie di fasi temporali studiate per simulare il passaggio dell’impronta attraverso il contatto di rotolamento (ved. [5]). Da questo processo di simulazione in più fasi, la storia delle sollecitazioni di fatica e il criterio di fatica, possono essere impiegati per ulteriori elaborazioni, al fine di stimare l’affaticamento che si accumula dall’inizio fino al ciclo di carico corrente. Lo schema segue fedelmente lo stesso processo di elaborazione dei dati presentato da Morales-Espejel e Brizmer [8]. Il danneggiamento complessivo accumulato fino al ciclo di carico corrente si calcola con la regola di Palmgren-Miner.

Quando la fatica raggiunge un valore critico si instaura la possibilità di una frattura del materiale. Lo schema attuale non si avvale di un modello dettagliato di propagazione delle cricche; il danneggiamento progressivo viene simulato semplicemente rimuovendo il materiale affaticato. A tale scopo è stato implementato un modello semplice di distacco delle schegge del materiale affaticato [8] che ha il compito di rimuovere sia il materiale in cui il danneggiamento critico si è accumulato sia il materiale soprastante. Tale modello contiene anche una profondità limite (h) dalla superficie, al di sotto della quale al materiale con danneggiamento critico non è ammesso il distacco. Questa profondità limite può essere fissata tra h = 0 e h = ∞. Se si imposta h ≥ 0 si permette al materiale al di sotto della superficie di staccarsi. Il modello attuale non può dare un’indicazione precisa circa la crescita del danneggiamento se non si conosce preventivamente il parametro h o se non sono disponibili alcuni risultati sperimentali, ma può descrivere molto bene i campi di accrescimento del danneggiamento, come si vedrà in seguito. Il processo di calcolo viene ripetuto per un dato numero di cicli di carico (fino ad un numero massimo, normalmente > 10⁹ cicli di rotolamento), dopo di che si registra la storia del danneggiamento progressivo.

Risultati del modello
I dati dei test sono riportati nella tabella 1. In questo caso le impronte sono più ampie (ad es. con 400 µm di diametro) del contatto hertziano nella direzione di rotolamento (cioè 142 µm); durante il rotolamento è quindi impossibile che sull’impronta si crei la necessaria pressione EHL. Questo fatto provoca un collasso del film d’olio sui bordi della zona scheggiata. In tali condizioni si può escludere dall’analisi l’effetto del film lubrificante e il danneggiamento progressivo può essere simulato semplicemente adottando l’approssimazione rappresentata dal contatto a secco.

La fig. 6 mostra l’evoluzione della scheggiatura partendo dall’impronta iniziale al crescere del numero di giri; essa evidenzia anche i progressivi cambiamenti della pressione hertziana e delle relative sollecitazioni sotto la superficie. Le simulazioni numeriche mostrano chiaramente la direzione preferenziale della zona che si scheggia progressivamente. Il danneggiamento inizia dai bordi laterali dell’impronta e prosegue in direzione assiale attraverso la pista in modo analogo a quello osservato negli esperimenti (ved. fig. 4). Confrontando con il numero di giri del cuscinetto la zona coperta dal danneggiamento e la sua evoluzione, è possibile ottenere la curva di progressione della zona danneggiata. Questo è stato fatto per due livelli di profondità h, uno minimo e l’altro massimo, al fine di caratterizzare meglio lo scopo delle simulazioni (h_min semplicemente toccando la zona della sollecitazione massima ortogonale di taglio attorno all’impronta e h_max  ben oltre). Le curve risultanti sono indicate in fig. 5 con linee tratteggiate. La linea tratteggiata sottile è il risultato dell’impostazione più prudenziale nella stima della micro-scheggiatura a innesco superficiale, ossia al valore minimo del limite di profondità. I risultati della simulazione rappresentano quindi un limite di sicurezza del danneggiamento, che definisce le condizioni per determinare la massima zona di danneggiamento prevedibile, conseguente ad ogni scheggiatura ad innesco superficiale.

Se si introduce il valore massimo del limite di profondità h, l’evoluzione del danneggiamento, indicata di fig. 5 con una linea tratteggiata spessa, risulta corrispondere più realisticamente ai risultati sperimentali. Si noti l’andamento iniziale a gradini, chiaramente corrispondente ad alcune delle misurazioni pratiche. La curva mostra un andamento stabile di crescita tra 90 e 120 milioni di giri; questo intervallo può essere confrontato con la fase iniziale misurata di accrescimento del danneggiamento dell’impronta come discusso nel paragrafo “Lavoro sperimentale”.

La fig. 7 mostra l’andamento del danneggiamento negli esperimenti confrontato con quello che si ottiene con le simulazioni numeriche su 11,5 milioni di giri (134 milioni di cicli). Questa buona correlazione tra la media dei risultati sperimentali e le simulazioni numeriche dimostra la capacità del sistema di calcolo di considerare alcuni degli effetti principali dei meccanismi dell’affaticamento superficiale e dell’evoluzione delle scheggiature iniziali. I risultati sperimentali indicano una crescita accelerata dopo 100 milioni di giri, che sembra essere assente nei risultati delle simulazioni numeriche. Una spiegazione possibile di questo comportamento è che la formazione della zona scheggiata dia anche luogo a carichi aggiuntivi a seguito della risposta dinamica del cuscinetto alla scheggiatura. Al momento, questi carichi aggiuntivi non sono inclusi nel modello, cosicché solo la scheggiatura iniziale può essere ragionevolmente confrontata con le simulazioni numeriche.

Nei risultati delle simulazioni è anche interessante il meccanismo del danneggiamento progressivo. Dato che l’impronta è un po’ più grande della larghezza hertziana nella direzione del rotolamento, la zona più caricata della pista è quella laterale dell’impronta, dove effettivamente inizia e progredisce il danneggiamento. Questo meccanismo di propagazione si può anche trovare nella simulazione numerica, dalla quale si evidenzia come il bordo laterale della scheggiatura sia influenzato dalle maggiori sollecitazioni superficiali e dalle concentrazioni di sollecitazioni sotto la superficie (fig. 6). Questo tipo di propagazione delle scheggiature sembra essere tipico dei cuscinetti a rulli.

Discussione e conclusioni
Gli esperimenti sono stati condotti sui cuscinetti a rulli conici, creando impronte sulle piste con utensili di durezza definita. Questo dà luogo ad una serie di fenomeni di accrescimento delle sollecitazioni superficiali da cui si originano le scheggiature, permettendo uno studio dettagliato del loro innesco e successiva evoluzione. Per studiare il processo di macro-scheggiatura con innesco in superficie è stato adattato un modello esistente della fatica della micro-geometria e affaticamento superficiale, Morales-Espejel e Brizmer [8].

Il modello è stato applicato per acquisire migliori conoscenze sull’innesco e la prima fase di propagazione delle scheggiature. Dai risultati dei calcoli si nota che in realtà il modello numerico può simulare e spiegare bene molte delle osservazioni sperimentali. In particolare, il modello ha mostrato che, nel caso dei cuscinetti a rulli conici, le scheggiature si propagano inizialmente attraverso la pista, ossia lungo la direzione perpendicolare al rotolamento. In generale, nei cuscinetti con contatti lineari, le sollecitazioni sono più elevate sui bordi laterali dell’impronta. Tali sollecitazioni facilitano la crescita delle cricche e scheggiature attraverso la pista durante la loro espansione iniziale.

Dai risultati dell’attuale lavoro si possono trarre le seguenti conclusioni:

1) Nei cuscinetti a rulli le scheggiature provenienti dalle impronte artificialmente impresse si propagano inizialmente trasversalmente alla pista, favorite dalle sollecitazioni elevate riscontrabili sui bordi delle scheggiature stesse, lungo la direzione ortogonale al rotolamento, come in precedenza discusso nella letteratura.

2) Il modello presentato descrive bene i due meccanismi di propagazione delle scheggiature. In particolare per quanto riguarda quelle dei cuscinetti a rulli, esiste nell’andamento iniziale di crescita delle scheggiature, una buona correlazione tra le previsioni del modello e le misurazioni sperimentali.

Riconoscimenti
Il progetto è stato parzialmente finanziato dall’European Commission Marie Curie Industry-Academia Partnerships and Pathways (IAPP) – iBETTER Project.

http://cordis.europa.eu/project/rcn/109976_en.html

Bibliografia
[1] Lundberg, G. and Palmgren, A. (1947), “Dynamic Capacity of Rolling Bearings,” Acta Polytechnica, 1(3), pp 1–52.
[2] Lundberg, G. and Palmgren, A. (1952), “Dynamic Capacity of Roller Bearings,” Acta Polytechnica, 2(4), pp 96–127.
[3] Morales-Espejel, G. E. and Gabelli, A. (2011), “The Behavior of Indentation Marks in Rolling Sliding Elastohydrodynamically Lubricated Contacts,” Tribology Transactions, 54, pp 589–606.
[4] Morales-Espejel, G.E., Gabelli, A. de Vries A. (2015), “A Model for Rolling Bearing Life with Surface and Subsurface Survival – Tribological Effects”, to be published at Tribology Transactions.
[5] Morales-Espejel, G.E. and Gabelli, A. (2015), “Il modello generalizzato SKF
della durata, potenza della tribologia,”
Evolution #4-2015, pp 22-28.
[6] Morales-Espejel, G.E. e Gabelli, A. (2015), “The Progression of Surface Rolling Contact Fatigue Damage of Rolling Bearings with Artificial Dents,” Tribology Transactions, 58, pp 418–431.
[7] Snare, B. (1970), “How Reliable Are Bearings?” The Ball Bearing Journal, 162, pp 3–7.
[8] Morales-Espejel, G. E. and Brizmer, V. (2011), “Micropitting Modelling in Rolling–Sliding Contacts: Application to Rolling Bearings,” Tribology Transactions, 54, pp 625–643.