La domanda di prodotti affidabili, leggeri e di prezzo competitivo, ha posto l’accento su una migliore prevedibilità delle prestazioni dei cuscinetti volventi in termini di durata. Ciò ha stimolato la ricerca e l’aggiornamento degli standard relativi al calcolo di tale durata, per tenere conto degli attuali progressi della tecnica.Gli standard attuali per il calcolo della durata dei cuscinetti risalgono al lavoro compiuto alla SKF nel 1947 da parte di Gustaf Lundberg e Arvid Palmgren. L’equazione della durata è stata elaborata sfruttando la teoria probabilistica della fatica, sviluppata da Weibull nel 1939, che ha consentito di tener conto dell’affidabilità del cuscinetto nel calcolo della durata. Ciò ha segnato un progresso decisivo nella disponibilità di metodi di calcolo progettuali per l’uso di questo essenziale organo meccanico.
La possibilità di stimare la durata e di scegliere, in modo razionale, un cuscinetto idoneo per una particolare applicazione è stata una fondamentale conquista dell’ingegneria. Da allora, la scienza e la tecnica, in particolare la tribologia, hanno compiuto enormi progressi. Oggi la progettazione dei cuscinetti si avvale delle migliori conoscenze teoriche e delle tecniche di calcolo più recenti. Ciò è favorito anche dall’impiego di computer sempre più potenti. Inoltre la moderna siderurgia è in grado di produrre acciai più puri e con composizioni più precise e omogenee. I lubrificanti, d’altro canto, sono migliorati, rendendo possibile una più efficace separazione delle superfici in movimento, mentre i metodi moderni di produzione in serie creano prodotti di alta precisione e con livelli di qualità sempre più elevati.
Questi progressi esigono che i calcoli di durata tengano conto delle migliori prestazioni oggi offerte dai cuscinetti. Nel corso degli anni, si è tenuto conto del miglioramento delle prestazioni principalmente mediante l’aumento del coefficiente di carico dinamico, che ha un effetto diretto sulla durata. Talvolta si sono introdotti fattori correttivi per tenere conto delle condizioni operative, come l’uso di materiali e lubrificanti speciali. Fino a poco tempo fa, tali calcoli di durata hanno soddisfatto l’industria abbastanza bene.
Tuttavia, le osservazioni effettuate sui principali meccanismi di cedimento dei moderni cuscinetti hanno apportato nuove conoscenze. Per esempio si è notato come i cedimenti per fatica abbiano inizio con maggiore frequenza sulla superficie delle piste, piuttosto che da cricche formatesi al disotto di questa. È stata quindi posta l’attenzione sull’influenza della finitura superficiale e della contaminazione da particelle estranee. Nei moderni acciai da cuscinetti è anche stata osservata l’esistenza di un limite di fatica.
Queste considerazioni hanno portato alla proposta di calcoli di durata più affinati e a pubblicazioni in cui si studiano appunto gli effetti della contaminazione e della finitura superficiale sulla durata del cuscinetto.
In particolare, il modello di durata a fatica pubblicato nel 1985 da Eustathios Ioannides e Tedric Harris introdusse due innovazioni alla teoria di Lundgren e Palmgren:

i) un valore di soglia della sollecitazione locale, vale a dire un limite di fatica, al disotto del quale non è previsto l’insorgere della fatica nel cuscinetto,

ii) il volume di materiale sollecitato nel contatto, considerato come un insieme di elementi di volume relativamente piccoli, ciascuno sottoposto a sollecitazioni locali individuali.

In tal modo, si possono introdurre nel calcolo della durata a fatica le reali sollecitazioni locali e i molteplici effetti provocati da concentrazioni di sollecitazioni sulla superficie di rotolamento. Queste possono essere le sollecitazioni ai bordi o quelle dovute a impronte da impurità. Naturalmente un approccio così puntuale esige programmi di calcolo complessi, dato che si deve valutare il rischio di cedimento su un campo di sollecitazioni piuttosto complicato. Non potendo accedere a tale tipo di risorse, molti utilizzatori preferiscono applicare le formule semplici che si trovano sui cataloghi dei costruttori di cuscinetti o nelle norme ISO.
Per venire incontro alle necessità degli utilizzatori e sfruttare i vantaggi offerti dai progressi tecnologici e dalle nuove conoscenze, è stata presentata l’equazione SKF della Durata , elaborata introducendo una sollecitazione reale efficace, mediata su tutto il volume a rischio. Il limite di fatica e l’effetto delle sollecitazioni locali sono stati introdotti in questa formulazione, usando equazioni simili a quelle sviluppate da Lundberg-Palmgren. In pratica, si introduce un fattore di sollecitazione che agisce sul limite di fatica del cuscinetto. Si tratta di un fattore che tiene conto della effettiva sollecitazione del cuscinetto, considerando le condizioni d’impiego reale. Naturalmente questo fattore non è presente nel campo delle sollecitazioni hertziane ideali, usate nella classica analisi di Lundberg-Palmgren. Questo approccio ha portato ad un’espressione semplificata, che può essere calcolata in modo analogo a quanto contenuto nella norma ISO 281 (1990).
L’equazione mantiene in misura notevole la semplicità originaria, sebbene descriva le prestazioni dei moderni cuscinetti in modo più preciso.

Formule standard della durata
Nella previsione della durata dei cuscinetti il modello della durata a fatica occupa una posizione centrale. Il modello tradizionale di danneggiamento cumulativo originato da cricche presuppone per le sollecitazioni una legge esponenziale per descrivere la porzione di durata spesa nell’avvio di una cricca, che, come noto, domina l’intera durata dei contatti volventi.
Nelle previsioni di durata dei cuscinetti si sono inizialmente applicati metodi probabilistici, a causa della naturale dispersione dei valori riscontrati nella pratica. Lundberg e Palmgren (1947) usarono la distribuzione probabilistica della fatica nei metalli di Weibull (1939) per stabilire la teoria di base della dispersione stocastica delle durate dei cuscinetti, come dimostra l’equazione seguente:

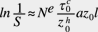        (1)

Sostituendo i parametri del contatto hertziano (in termini di carico applicato e geometria di contatto), essi ottennero una relazione carico-durata per i cuscinetti volventi, che, nella sua forma finale può essere espressa in modo molto semplice:

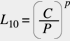        (2)

in cui C è il coefficiente di carico dinamico del cuscinetto, un fattore che dipende dalla geometria di quest’ultimo, e P è il carico equivalente sul cuscinetto stesso. L’esponente p vale 3 per i cuscinetti a sfere e 10/3 per i cuscinetti a rulli. La formula (2) è stata adottata dalla ISO nella raccomandazione R281 (1962). Nel 1977, sono stati introdotti i fattori correttivi a₁, a₂ e a₃ per tenere conto dei differenti livelli di affidabilità, proprietà alla fatica del materiale e lubrificazione, dando luogo alla formula standard di oggi, quella ISO 281 (1990):

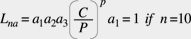        (3)

Molti produttori di cuscinetti, che hanno riconosciuto la correlazione tra il materiale e la lubrificazione, usano tale formula sotto la forma:

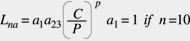        (4)

La Formula SKF della Durata
Una semplice formulazione analitica per la durata dei cuscinetti che considera la resistenza alla fatica del materiale è stata derivata dal modello della fatica dei contatti volventi, stabilito da Ioannides e Harris nel 1985.
Questo modello fu inizialmente applicato alle soluzioni numeriche del rischio di fatica di campi tridimensionali di sollecitazione di contatti volventi. A causa dell’evidente similitudine esistente tra i campi di sollecitazione hertziani, si è pensato che, nel caso di contatti per l’appunto strettamente hertziani, una semplificazione era possibile. Questo viene realizzato usando un criterio di sollecitazione basato sul valore massimo dell’ampiezza della sollecitazione ortogonale di taglio t₀, oltre un valore di soglia, e introducendo una sollecitazione limite di fatica tu del contatto volvente . Così l’uso della sollecitazione limite di fatica t_u, può essere realizzato tramite la sostituzione dell’ampiezza della sollecitazione di taglio t₀, del campo di sollecitazione hertziano della equazione (1) con la differenza t₀, – t_u, . Pertanto l’equazione (1) diventa:

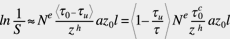        (5)

Nella formulazione di cui sopra, per le parentesi si usa la notazione Macauley; in altre parole il termine vale zero se la quantità racchiusa è negativa. Per ottenere l’equazione della durata per i cuscinetti volventi, in presenza di un limite di fatica del materiale, si può usare l’equazione (5), la quale differisce da quella originaria di Lundberg e Palmgren (1) solo per le parentesi Macauley di destra. È quindi possibile eseguire le stesse operazioni per la derivazione della capacità dinamica dei cuscinetti come descritto nel lavoro originario di Lundberg e Palmgren. Applicando la nota relazione fra le sollecitazioni indotte e il carico applicato per i contatti di tipo hertziano, sia puntiforme che lineare, come fatto da Lundberg e Palmgren nel 1947, si ottiene un’equazione corrispondente alla (5), ma scritta in termini di carico equivalente e di coefficiente di carico. Per una probabilità di cedimento del dieci per cento, la corrispondente durata del cuscinetto si esprime con la formula :

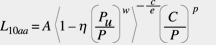         (6)

in cui il parametro h è un fattore (corrispondente ad un fattore di sollecitazione) introdotto per tenere conto delle effettive sollecitazioni presenti nei contatti in condizioni operative reali del cuscinetto. Naturalmente questo parametro non può essere calcolato usando le sollecitazioni hertziane ideali, applicate nella derivazione della equazione originaria di Lundberg e Palmgren del 1947. Inoltre si può dimostrare che, oltre alle sollecitazioni dovute al trattamento termico e al montaggio, il fattore di sollecitazione h dipende in larga misura dalle condizioni di lubrificazione del contatto e dalla concentrazione di sollecitazioni su scala microscopica dovuta a impronte o imperfezioni. Di conseguenza, h è dato in funzione delle condizioni ambientali, (lubrificazione e contaminazione) e delle dimensioni del cuscinetto.

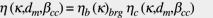         (7)

Introducendo l’equazione (7) nella (6) si ottiene:

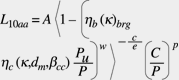         (8)

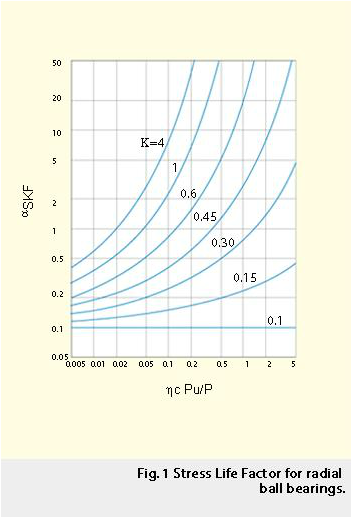
Per semplificare l’uso dell’equazione precedente, nel 1989 la SKF introdusse un fattore a_SKF per ogni classe di cuscinetti, radiali a sfere, radiali a rulli, assiali a sfere, assiali a rulli. Tale fattore si può calcolare e mettere in diagramma come mostrato in fig. 1:

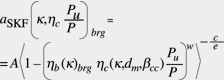        (9)

Sono state anche derivate curve della
funzione h_c(k, d_m, b_cc), come spiegato da Bergling e Ioannides (1994) e da Ioannides e colleghi (1999) . Esempi di tali curve parametriche sono rappresentati in fig. 2. Con tali informazioni l’equazione (8) della durata si può scrivere in modo semplice:

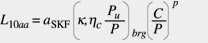        (10)

Questa è l’equazione della durata usata nel Catalogo generale SKF dal 1989. Questa equazione, assieme ai diagrammi delle figure 1 e 2, può essere utilizzata per calcolare la durata dei cuscinetti volventi in maniera diretta, simile a quella indicata nella norma ISO 281 (1990). Tuttavia, l’equazione (10) può tenere conto di condizioni particolari di lubrificazione e contaminazione e degli incrementi di durata sperimentabili su cuscinetti non eccessivamente caricati e ben lubrificati con lubrificante pulito.

Verifiche sperimentali
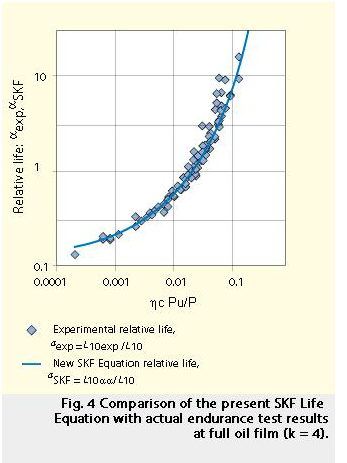
Per verificare la precisione l’equazione SKF della durata dei cuscinetti (l’equazione 10) sono state effettuate numerose prove su più di 8.000 cuscinetti in varie condizioni di carico, lubrificazione e contaminazione. La fig. 3 presenta una panoramica delle durate medie L₁₀ rilevate in tali prove. È stato fatto un confronto tra le durate previste e quelle effettivamente riscontrate, riportate in fig. 3, diagrammando il rapporto della durata sperimentale sulla durata teorica di base, ossia di a_exp=L_10exp/L₁₀, in funzione del corrispondente parametro h_c P_u/P.
In fig. 4, è riportato un gruppo di punti ottenuti sperimentalmente, relativi a cuscinetti a sfere operanti in presenza di un film completamente formato. I vari punti appaiono sovrapporsi in gran parte alla corrispondente curva di a_SKF relativa alla durata calcolata con l’equazione (9). La fig. 4 mostra una buona concordanza fra la durata relativa calcolata con l’equazione SKF e i risultati sperimentali. Una valutazione più approfondita di questi ultimi ha anche indicato che, usando l’equazione SKF, il divario totale nel calcolo della durata può essere dimezzato, rispetto ai risultati degli stessi calcoli basati esclusivamente sui coefficienti di carico dinamico standard dei cuscinetti. Questa migliore precisione e corrispondenza fra i dati teorici e quelli sperimentali conferma la scelta delle costanti usate nello sviluppo del modello analitico e applicate nell’equazione SKF della durata. Inoltre, il trend asintotico presentato dalla funzione askf (k, h_c P_u/P), figure 1 e 4, al tendere del parametro h_c P_u/P verso condizioni di minori sollecitazioni nel cuscinetto, è un’ulteriore conferma del limite di sollecitazione di fatica ipotizzato per i contatti di tipo volvente. L’andamento della curva di askf (sollecitazione relativa rispetto a durata relativa) è in verità simile a quello delle familiari curve di Wöhler (sollecitazione rispetto al numero di cicli di sollecitazione) usate per diagrammare la probabilità di sopravvivenza di campioni soggetti a prove di fatica con differenti livelli di sollecitazione.

Conclusioni
I cuscinetti hanno reso possibile l’uso di forti carichi ad alta velocità, con un buon livello di affidabilità e un attrito minimo, rendendo possibile l’intenso processo di meccanizzazione che ha caratterizzato il recente sviluppo industriale, rivoluzionando profondamente il nostro modo di vivere. La disponibilità di strumenti adatti per la scelta e l’impiego dei cuscinetti può incidere in modo considerevole su funzionamento, rendimento e costo delle macchine. L’equazione SKF della durata introduce un nuovo e più valido standard per la previsione delle prestazioni dei cuscinetti e risponde alle continue richieste di migliori metodi di progettazione, scelta e uso dei cuscinetti.
Usando solamente alcuni parametri essenziali e concentrandosi su quei fattori che sono veramente decisivi per le prestazioni, l’equazione SKF della durata riesce a descrivere il complesso sistema tribologico nel quale operano i cuscinetti. Inoltre l’equazione considera che gli effetti, in termini di fatica, derivanti da tali fattori non possono essere descritti come una sovrapposizione semplicistica dei rischi indotti dai vari tipi di sollecitazioni considerati separatamente. Quindi, anziché cercare di derivare fattori di lubrificazione, contaminazione, ecc. capaci di influire indipendentemente sulla durata, L’equazione SKF della Durata introduce un singolo fattore a carattere multidimensionale a_SKF = f (k, h_c P_u/P), dipendente da quelle quantità che sono veramente importanti per lo stato tribo-fisico del sistema. Questo approccio permette di sfruttare al meglio i dati disponibili dell’applicazione, a tutto vantaggio del progettista e dell’utilizzatore della macchina. La corrispondenza con i risultati sperimentali e la migliore precisione ottenuta usando l’equazione SKF della durata giustifica l’adozione di tale approccio per i calcoli di previsione della durata dei moderni cuscinetti volventi.

Ioannides E., Bergling G. e Gabelli A. “An analytical formulation for the life of rolling bearings” .Acta Polytechnica Scandinavica, ME 137, Espoo (1999).

Eustathios Ioannides, SKF Engineering & Research Centre (ERC), Nieuwegein,
Olanda, e Imperial College of Science & Technology, Londra, UK;
Gunnar Bergling, AB SKF, Göteborg, Svezia,
e Antonio Gabelli, SKF Engineering & Research Centre (ERC), Nieuwegein, Olanda.