滚动接触疲劳是滚动轴承和类似机器零件的一种典型失效模式。Lundberg和Palmgren完成了滚动接触疲劳研究的基础工作[1], [2]。Lundberg-Palmgren理论主要关注次表面滚动接触疲劳，且完全依赖于理想光滑赫兹应力计算。相反，表面滚动接触疲劳涉及靠近接触表面（几微米深）的区域，该区域受到粗糙度、外形偏差、压痕等表面形状特点产生的局部表面牵引力和应力的强烈影响。弹性液动润滑薄膜与决定表面应力集中的实际特征的相互作用，对了解滚动轴承表面疲劳现象非常重要（Morales-Espejel和Gabell[3]）。本文通过对接触面和与产生应力集中的表面微观形状偏差的相互作用进行建模，研究了表面滚动接触疲劳的演变过程。本文对数字仿真与一组试验结果进行了比较，发现它们具有很好的关联性，这使得有关表面滚动接触疲劳以及它在滚动轴承中出现和增长的基础机理的假说得以成立。这个新知识非常符合SKF通用轴承寿命模型（SKF Generalized Bearing Life Model）背后的基本思想，后者是把表面与次表面疲劳损伤分离开来进行研究[4] [5]。

损伤演变过程的理论研究
起源于表面微观形状特征的滚动接触疲劳损伤，通常会发展成剥落。高级形式的剥落扩展，受到宏观形状方面的强烈影响，例如，滚道接触形状的演变和滚动轴承中出现的总应力场。几名研究者已经研究了滚动轴承的剥落扩展，试图将其与促进损伤演变的机械方面关联起来。

本文作者[6]在一项最新研究中同时使用模型和试验方法，研究了预先刻出凹痕的滚动轴承的表面滚动接触疲劳的演变过程， 结论是球轴承涉及的机理要求考虑润滑条件以及表面与次表面应力的相互作用，来了解沿滚道的典型V形裂纹的发展，这不同于在滚子轴承中观察到的初始横向损伤增长，后者用干摩擦接触假设就能得到充分解释。

损伤演变过程的试验观察
Snare [7]在他的轴承可靠性统计分析中，监测了圆柱滚子轴承的一处剥落的扩展，显示出在剥落开始沿滚道扩展前损伤就横穿滚道的清晰演变过程。图1列出了Snare的试验测试。

现有了解
从文献记载的理论和试验研究中，能够明确识别出至少两个表面缺陷导致的剥落扩展阶段。第一个阶段是剥落以较低的速度横穿滚道增长，第二个是以加速的方式沿着滚动路线增长。在初始阶段剥落之所以横穿滚道扩展，被认为是因为剥落的直径边缘出现的应力（方向垂直于滚动方向）要高于剥落头和尾边缘的应力。

球轴承（图2）和滚子轴承（图3）剥落出现和扩展的行为是明显不同的。球轴承中由表面引起的剥落，初始是在压痕的尾部边缘呈现独特的V形，然后在滚动方向快速增长，同时V形区域的滚道材料出现剥落。剥落的增长是在滚动方向上观察到的，该方向与剥落位置出现的摩擦和滑动的方向相反（图2）。滚子轴承中由表面引起的剥落发源于早期损伤处并向两侧扩展，然后垂直于滚道增长，再沿着滚道扩展（图3）。

本文的目的是进一步揭示滚子轴承表面疲劳损伤的演变过程。通过对试验观察到的损伤进行建模来进一步了解其扩展的驱动机理，是文本作者[3] 所发表工作的继续。之前这项工作专注于初始损伤阶段，但现在专注损伤的演变过程。

试验工作
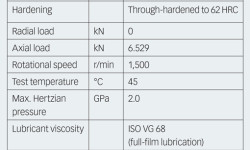
试验采用标准圆锥滚子轴承，见表1。

使用1,250 N压痕载荷和直径1毫米的碳化钨球压头，人为在圆锥滚子轴承上制造出压痕。这个载荷产生直径400微米、深30微米、边缘凸起高度约2微米的压痕。在这个试验中，沿着圆锥滚子轴承内圈的圆周上均等间隔分布8个压痕。此外，这些压痕在垂直滚道方向上，从滚道边缘开始，以0.5毫米的阶跃间隔。不过，本文只详细讨论位于滚道中心的压痕的损伤演变过程。在表1的工作条件下，轴向载荷在滚动方向上产生约142微米的赫兹宽度，它要比压痕直径窄得多。试验在不同转数下进行，以观察压痕的应力集中和润滑条件造成的疲劳损伤的演变过程。

图4列出了圆锥滚子轴承在不断增加转数情况下压痕剥落演变过程的试验结果。剥落起初出现在压痕的一侧，然后横穿滚道朝着压痕两侧扩展，也就是说，扩展方向垂直于滚动方向。图4(b)画出一个近似接触椭圆，以与最终剥落比较。每隔约500万转，定期用显微镜检查多个轴承内圈，来确定剥落的初始阶段和扩展阶段。对每个压痕进行显微镜检查和照相，并将压痕状况作为试验中转速的函数。收集单独的压痕的显微照片并进行数字图像处理，来测量压痕周围的剥落区域的初始发展和进一步扩展。这个详细研究的结果给出了有关剥落损伤
面积的产生和扩展与转数之间关系的精确信息。图5列出了从出现剥落损伤的6个压痕收集的所有数据。

对平均试验数据的更详细研究表明，剥落区域的演变是一个包含三个阶段的过程：1. 潜伏阶段：持续5,000-6,000万转，未在轴承滚道上检测到明显的可见损伤，这大约是轴承的额定疲劳寿命。2. 初始损伤演变阶段：持续3,000-4,000万转，如同预计的一样，损伤面积出现指数式增长。3. 加速增长阶段：持续2,000-2,500万转，此期间的增长率显著加快（是上个阶段的两倍多）。

损伤扩展模型
滚动接触损伤的计算是引入能严格再现实际压痕的参数分析函数，首先对滚道的初始压痕进行建模。

然后把压痕形状纳入滚动接触模型来再现实际试验轴承的赫兹循环应力。损伤演变过程计算采用由Morales-Espejel和Brizmer [8]以前开发的基本表面疲劳和剥落模型，如下详述。不过，对模型也做了一些改进和调整。例如，关闭了[8]中介绍的磨损计算例行程序以加快数字仿真的速度。关闭了快速润滑模型，并且对初始压痕宽于滚动方向赫兹接触点的情况（就是图4a中仿真的圆锥滚子轴承的情况），只采用干摩擦接触模型。然后用该模型计算整体压力和应力。这个近似是合理的，因为在这种情况下，润滑剂有可能从压痕和接触点流失。预计在压痕边缘区域不会产生液动压力，因此可以使用干摩擦接触假设对此压力建模（对于赫兹接触面积较宽的球轴承，就不能忽略润滑模型）。

一旦计算出接触压力，从一系列时间步长中就能获得应力发展情况，这些时间步长用来仿真压痕穿过滚动接触区域的路径（见[5]）。通过该多步仿真过程，可以进一步通过疲劳标准处理来计算疲劳应力的发展过程，从而预计从开始到当前载荷周期所累积的疲劳损伤。这个数据处理的方法，与Morales-Espejel和Brizmer介绍的一样[8]。从开始到当前载荷周期累积的总损伤是用Palmgren-Miner准则计算的。

当疲劳达到临界损伤值，材料断裂的可能性就出现了。现有的研究方法没有提供详细的裂纹扩展模型，损伤扩展是用简单去除疲劳材料来仿真的。为此，建立了一个简单的材料分离模型[8]，负责去除达到累积临界损伤的材料及其上面的材料。这个模型还含有一个距离表面的阈值深度（h），它下面的达到临界损伤的材料不允许被去除。这个阈值深度可以设置成从h = 0到h = ∞。设置h ≥ 0将允许分离表面下材料。如果无法提前知道系数h或一些试验结果无法获得，现有模型无法精确说明损伤增长，但它能非常好地说明下面介绍的损伤增长范围。计算过程以给定的载荷周期数量重复（最多到最大值，通常为>10⁹滚动周期），之后报告损伤演变过程。

模型结果
测试数据如表1所示。在这种情况下，压痕（即直径400微米）宽于滚动方向的赫兹接触点（即142微米），因此滚动过程中不可能在压痕上产生所需的弹性液动压力。这将破坏在压痕区域边缘的油膜。该条件下，可在分析中排除润滑油膜的影响，仅用干摩擦接触模型近似模拟损伤的演变过程。

图6显示了在转数不断增加时，初始压痕的剥落演化，以及赫兹压力和相关次表面应力的渐进变化。数字仿真的结果清楚显示了剥落区域演变过程的优先方向。损伤开始于压痕侧边缘，沿轴向穿过滚道发展，与试验观察到的方式类似（见图4）。通过计算损伤覆盖的面积以及它随轴承转数的演变，可以获得损伤面积相对轴承转数的演变过程曲线。计算是为获得两个阈值深度水平，即h的最小值和最大值，来描述模型仿真的范围（hmin表示接触到压痕周围的最大剪应力区域时的深度值，而hmax则表示远离这个区域的深度值）。获得的损伤演变过程曲线见图5的虚线。细虚线表示在最保守设置下的表面微剥落的结果，即阈值深度的最小值。因此，仿真结果代表损伤的安全界限，确定了任何表面剥落导致的最大预计损伤面积的条件。

图5粗虚线表示了在引入阈值深度h的最大值时，损伤的演变过程，该虚线与实际试验结果更加相符。显而易见的是计算损伤面积的初始趋势，显示出逐步的演变过程，完全符合一系列试验测量结果。在9,000万至1.2亿万转时趋势达到稳定增长率，这个间隔可与“试验工作”部分讨论的压痕损伤增长的测量初始演变阶段相当。

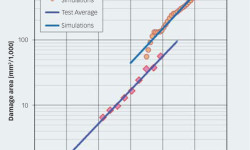
图7显示试验的损伤增长率与数字仿真中获得的一个损伤增长率的对比，数字仿真进行了1,150万转（1.34亿周期）。试验结果平均值与数字仿真具有很好的相关性，这表示该计算能够体现出表面疲劳机理和初始剥落演变过程的一些主要影响。此外，试验结果表明在1亿转以后损伤增长率出现加速增长，而数字仿真似乎没有得到这一结论。这个现象的一个可能的解释是，轴承会对剥落区域产生动态响应，承受由剥落导致的额外载荷。目前，这些额外载荷没有被纳入模型，因此只有初始剥落损伤试验可以很好地与数字仿真相比较。

在仿真结果中，损伤演变过程的机理也令人感兴趣。因为该压痕比滚动方向的赫兹宽度略宽，滚道上载荷最大的区域是压痕的侧面，这是损伤实际出现和扩展的地方。这个扩展机理在显示受最大表面压力和次表面应力集中影响的剥落的侧边缘的数字仿真中也能发现（图6）。这种剥落扩展似乎是滚子轴承所特有的。

讨论和结论
该试验在圆锥滚子轴承上进行。用预先规定硬度的标记物在轴承滚道上产生压痕。这导致出现一系列表面应力集中，剥落从这些地方发生，从而允许对它们的发生和演变过程进行详细研究。采用了一个现有的表面微观形状疲劳模型（Morales-Espejel和Brizmer [8]; 即表面损坏）来研究起源于表面的宏观剥落过程。

采用这个模型是为了更好地认识剥落的发生和早期扩展阶段。从计算结果发现，数字模型的确可以对许多试验结果进行很好的仿真和解释，特别是试验结果指出对圆锥滚子轴承，剥落初始是横穿滚道扩展的，也就是沿着与滚动方向垂直的方向扩展。对线接触轴承来说，压痕侧边缘的应力通常较高。在剥落初始扩展期内，这些较高的应力会促进剥落横穿滚道增长。

可从现有工作结果得出下面几条结论：

1. 如文献先前描述的一样，已产生压痕的滚子轴承的剥落，初始是横穿滚道扩展的，是受到剥落边缘处与滚动方向垂直的较高应力所推动的。

2. 本文提出的模型很好地说明了两个剥落扩展机理。特别是对滚子轴承，研究发现初始剥落增长率的模型预测与试验结果有很好的关联性。

致谢
本项目的部分资金来自欧洲委员会居里夫人产学合作和途径(IAPP) –iBETTER项目。

http://cordis.europa.eu/project/rcn/109976_en.html

参考文献
[1] Lundberg, G. and Palmgren, A. (1947), “Dynamic Capacity of Rolling Bearings,” Acta Polytechnica, 1(3), pp 1–52.
[2] Lundberg, G. and Palmgren, A. (1952), “Dynamic Capacity of Roller Bearings,” Acta Polytechnica, 2(4), pp 96–127.
[3] Morales-Espejel, G. E. and Gabelli, A. (2011), “The Behavior of Indentation Marks in Rolling Sliding Elastohydrodynamically Lubricated Contacts,” Tribology Transactions, 54, pp 589–606.
[4] Morales-Espejel, G.E., Gabelli, A. de Vries A. (2015), “A Model for Rolling Bearing Life with Surface and Subsurface Survival – Tribological Effects”, to be published at Tribology Transactions.
[5] Morales-Espejel, G.E. and Gabelli, A. (2015), “The SKF Generalized Bearing Life Model – the power of tribology,” Evolution #4-2015, pp 22-28.
[6] Morales-Espejel, G.E. and Gabelli, A. (2015), “The Progression of Surface Rolling Contact Fatigue Damage of Rolling Bearings with Artificial Dents,” Tribology Transactions, 58, pp 418–431.
[7] Snare, B. (1970), “How Reliable Are Bearings?” The Ball Bearing Journal, 162, pp 3–7.
[8] Morales-Espejel, G. E. and Brizmer, V. (2011), “Micropitting Modelling in Rolling–Sliding Contacts: Application to Rolling Bearings,” Tribology Transactions, 54, pp 625–643.