Comprender las imperfecciones del material
Los investigadores de SKF han trabajado constantemente para comprender mejor los efectos que tienen sobre el rendimiento de los rodamientos la microestructura y las imperfecciones preexistentes en el material. El presente estudio es fundamental para definir qué características y clases de severidad relacionadas tienen una influencia crítica en el rendimiento de los rodamientos.
Actualmente, las fallas de rodamientos debidas a fatiga por contacto rodante (rolling contact fatigue, RCF) son, en general, poco frecuentes, y normalmente la vida útil final que alcanzan los rodamientos supera la vida nominal calculada. No obstante, hay casos en aplicaciones específicas en las que los rodamientos pueden fallar prematuramente. Comprender los mecanismos de fallas en los rodamientos es fundamental para una mejora continua de su rendimiento, en respuesta a los requisitos que impone el constante incremento de la densidad de potencia en aplicaciones de rodamientos modernas.
La confiabilidad de los rodamientos en diversas aplicaciones obedece al principio del eslabón más débil, es decir, las fallas se producen como resultado de una rotura en el elemento más débil del sistema en cuestión. En condiciones de lubricación deficientes, las fallas en los rodamientos pueden deberse a daños por deformación en la superficie o desgaste. En otro caso, el eslabón más débil podría existir en la región de la subsuperficie. Ello se debe a la tensión cortante que se produce al alcanzar el contacto herciano su valor máximo a una determinada profundidad por debajo de la superficie del camino de rodadura. Además, al igual que la mayoría de los materiales de alta resistencia, los aceros de rodamientos, en general, pueden acusar una falta de tolerancia a daños en forma de sensibilidad a imperfecciones preexistentes en el material, por ejemplo, inclusiones no metálicas como un subproducto de los procesos de producción del acero.
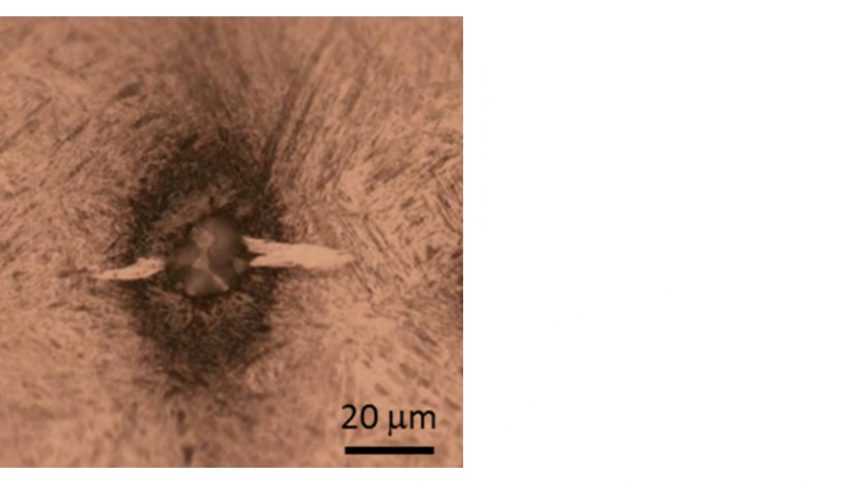
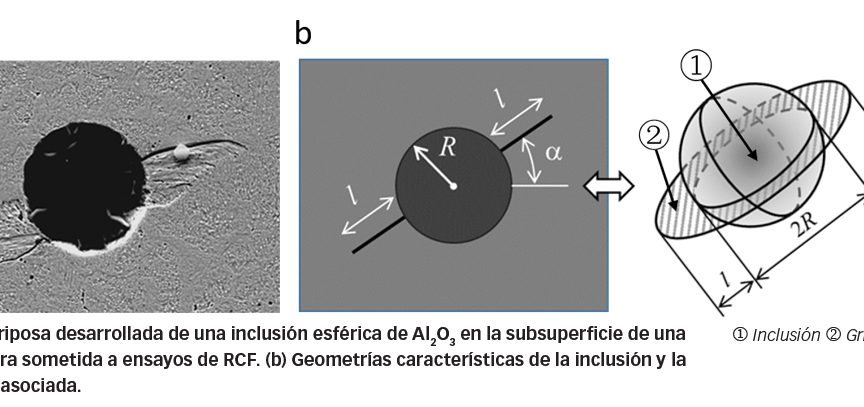
Investigaciones metalográficas en muestras sometidas a ensayos de RCF indican que las denominadas mariposas suelen desarrollarse a causa de inclusiones no metálicas. La mariposa procedente de una muestra atacada con nital observada con un microscopio óptico muestra un par de grietas que proceden de una inclusión, decoradas con una zona blanca de corrosión ácida, tal como se muestra en la fig. 1. La zona blanca de corrosión ácida es la microestructura alterada resultante de roce entre las caras de la grieta [1,2]. La grieta, bajo carga de contacto rodante, puede propagarse y eventualmente romper la superficie del camino de rodadura, lo que conduce al desconchado.
Imperfecciones del material en RCF
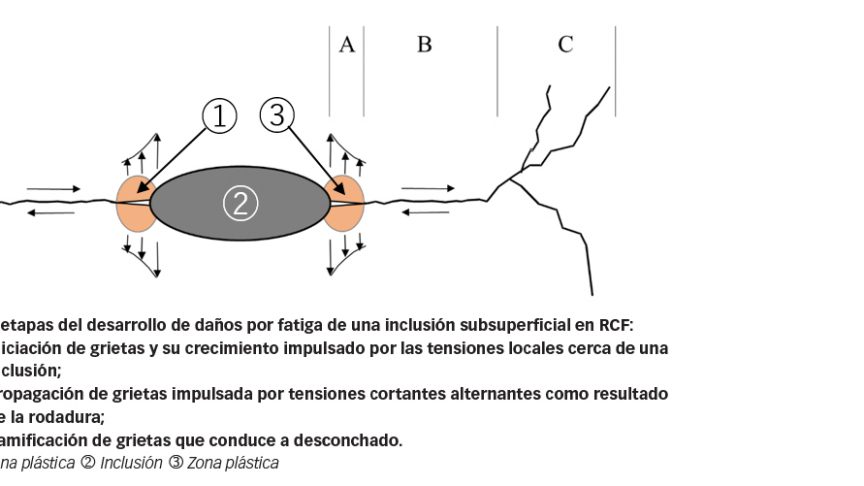
El contacto rodante en superficies de caminos de rodadura de rodamientos ocasiona tensiones cíclicas que se extienden desde la superficie hasta la subsuperficie. Debido al efecto del incremento de las tensiones, las grietas pueden iniciarse a causa de inclusiones, incluso bajo una presión de contacto inferior al llamado límite de prueba elástica (elastic shakedown limit), es decir, una presión de contacto por debajo de la cual todo el material, a excepción de las zonas próximas a inclusiones, se comporta elásticamente. Tal como se describe en la fig. 2, el proceso de los daños implica tres etapas que gradualmente pueden conducir al desconchado de la superficie del camino de rodadura del rodamiento.
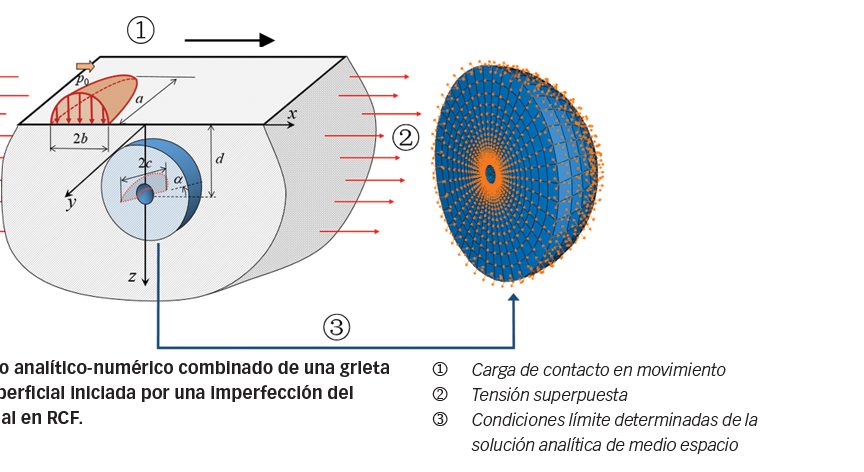
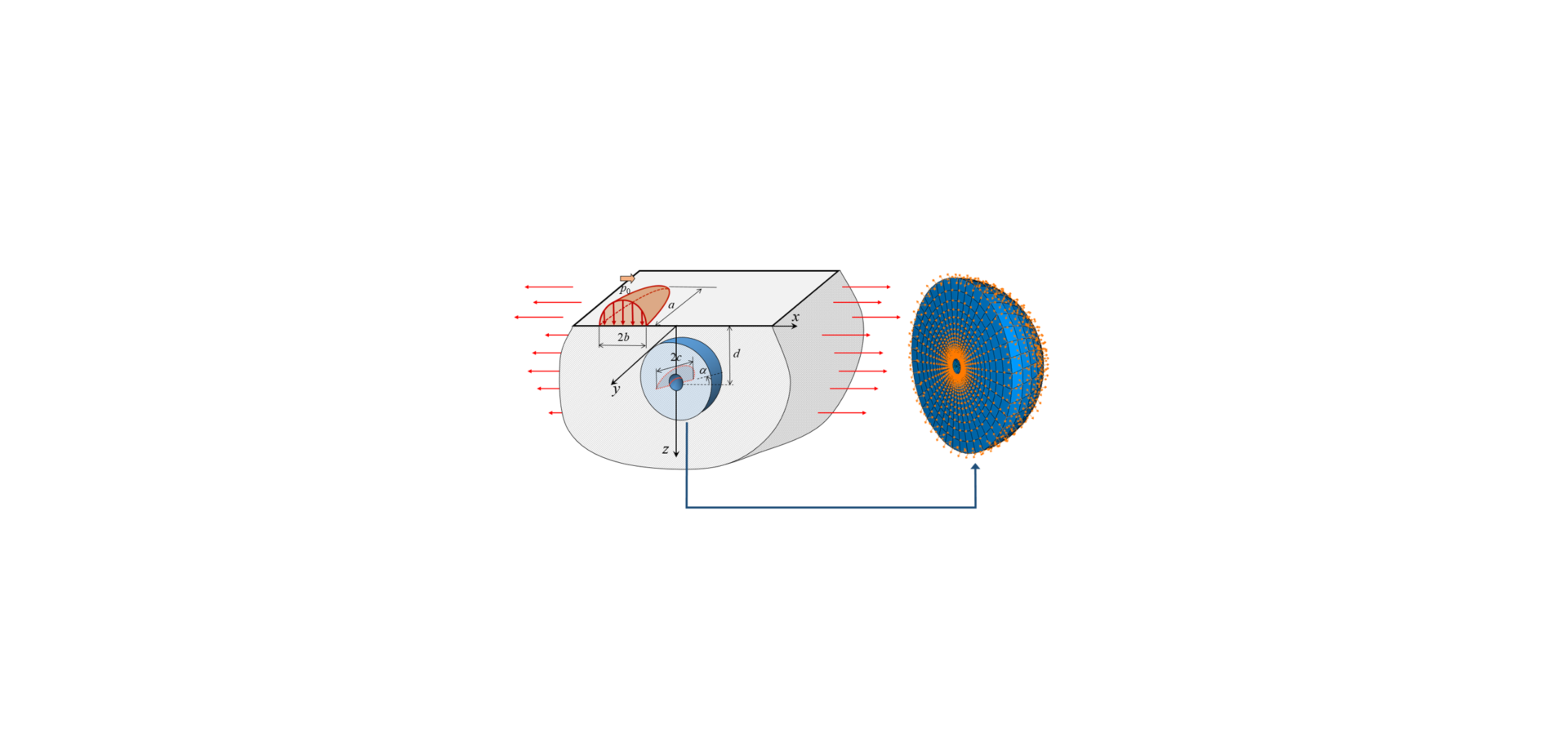
Se ha desarrollado una nueva metodología que combina la modelización con elementos finitos (FEM) con una solución analítica de un medio espacio sometido a carga en la superficie. Tal como se ilustra en la fig. 3, el FEM modeliza una capa de material rodeando el defecto, mientras que las tensiones en la subsuperficie y la deformación producida por el contacto rodante son “transmitidas” por los nodos limítrofes, en los cuales se prescriben los desplazamientos usando la solución analítica de medio espacio [3].
Se han tenido en consideración diferentes tipos de inclusiones en términos de composición o morfología, y las condiciones de ligazón entre inclusiones y matriz de acero. La simulación de FE también incorpora el comportamiento elástico-plástico de los aceros de rodamientos que responde de la plasticidad localizada.
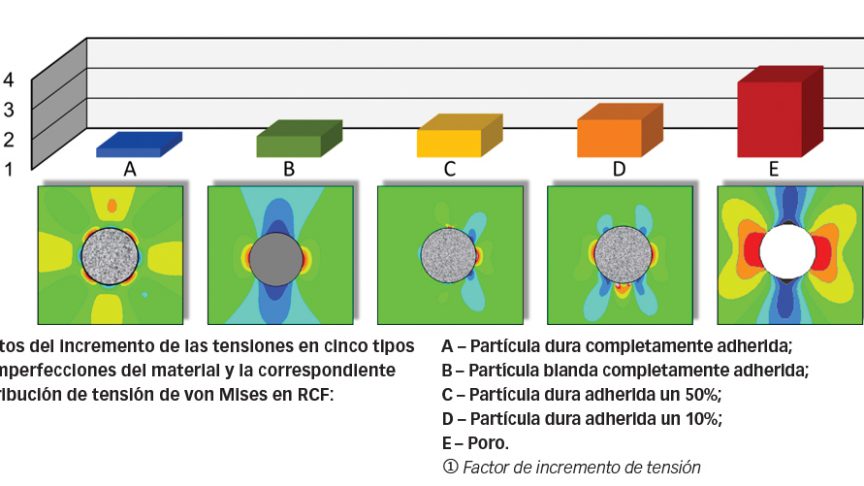
La fig. 4 muestra los factores del incremento de tensiones calculado de varias imperfecciones del material bajo RCF, incluidas partículas blandas y duras, y un poro. Las partículas se consideran como sólidos elásticos con una rigidez diferente de la de la matriz de acero. La fig. 4 también muestra la distribución de tensión de von Mises cerca de cada una de las inclusiones. La inclusión completamente adherida tiene un factor de incremento de tensiones relativamente bajo. Una partícula blanda completamente adherida tiene un factor de incremento de tensiones mayor que el de una inclusión dura completamente adherida. El factor de incremento de tensiones aumenta con la extensión del despegue entre la inclusión y la matriz de acero. Un poro es el caso extremo que posee el máximo factor de incremento de las tensiones.
La concentración de tensiones cerca de la inclusión puede causar plasticidad local en el acero, lo cual induce una tensión residual de tracción localizada. La tensión residual de tracción, junto con otros componentes de la tensión local cerca de la inclusión, puede causar la iniciación de grietas y la propagación de grietas inicial, es decir, la etapa A de daños por fatiga indicados en la fig. 2. La severidad del incremento de tensión mostrada en la fig. 4 indica la nocividad de diferentes inclusiones. Se ha comprobado que las partículas de nitruro de titanio, que normalmente están bien adheridas a la matriz de acero del rodamiento, son mucho menos dañinas que las inclusiones de óxido de aluminio, que también son partículas duras, pero tienen una adherencia deficiente con la matriz de acero, incluso despegadas.
Bajo una presión de contacto especificada, la iniciación de una grieta de una inclusión depende principalmente de la tensión local cerca de la inclusión. En otras palabras, la iniciación de una grieta está determinada por el tipo de inclusión, no por su tamaño, debido a que el factor de incremento de la tensión es independiente del tamaño de la inclusión. No obstante, una grieta iniciada por una inclusión no siempre se desarrollará en forma de desconchado. En ciertas circunstancias, la grieta puede detenerse permanentemente.
El crecimiento de grietas por fatiga se analiza dentro del marco de la mecánica de fracturas. La fuerza que impulsa el crecimiento de grietas por fatiga puede calcularse teniendo en cuenta los tamaños de la grieta e inclusiones de un tipo específico, y la tensión subsuperficial como resultado del contacto herciano y tensiones superpuestas como tensiones residuales, tensiones estructurales y/o circunferenciales, tal como se indica en la fig. 3. Si esa fuerza supera un determinado valor umbral, la grieta se propagará y terminará ocasionando una falla. En otro caso, la grieta se detendrá. Cuanto más elevada sea la fuerza impulsora, más rápidamente se propagará la grieta.
Considérese, por ejemplo, una inclusión esférica con un radio R y con una grieta anular de longitud l, tal como se indica en la fig. 5. La fuerza impulsora es proporcional a p0 √(R + l) donde p0 es la presión de contacto. Esto significa que la fuerza impulsora crece con la presión de contacto. Con una p0 especificada, el tamaño R de la inclusión determina la velocidad de crecimiento de la grieta, en especial durante la fase A, donde l es muy inferior a R. La influencia de la inclusión disminuye cuando la propagación de la grieta se aleja de la inclusión.
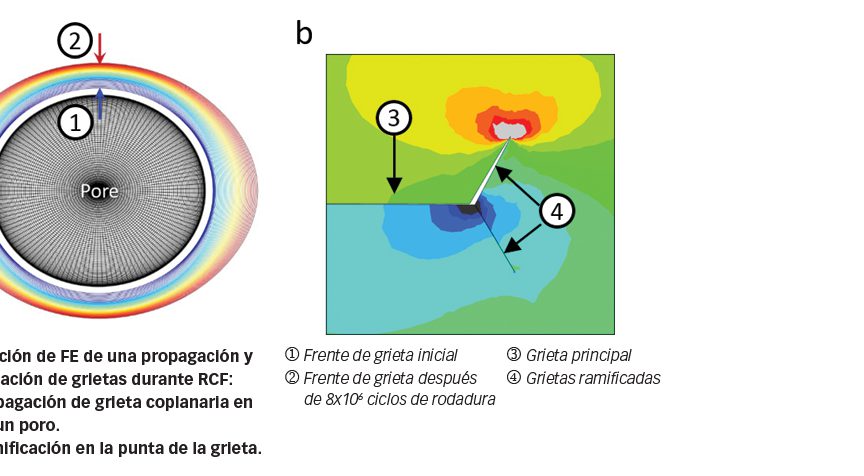
El análisis de elementos finitos se ha realizado para simular la propagación de una grieta 3D de un poro elipsoidal que representa una inclusión despegada por RCF. La propagación de grieta simulada, tal como se muestra en la fig. 6a, se comparó con la configuración de grieta observada en experimentos con RCF. Se comprobó una concordancia cualitativa entre el pronóstico y el experimento.
La propagación en la etapa B es impulsada principalmente por la alternancia de la tensión cortante que procede del contacto rodante, que más pronto o más tarde conduce a la propagación de la grieta de la etapa C, es decir, a su ramificación debido a una zona de tensión de tracción-compresión alternante en las proximidades de la punta de la grieta, tal como se muestra en la fig. 6b. Hay una pugna entre el crecimiento de grieta coplanaria del modo cortante y la ramificación de grieta del modo de tracción. La existencia de ramificación de grieta puede recibir el efecto de tensiones superpuestas. Una tensión de tracción fomenta la ramificación de las grietas y puede reducir la vida de fatiga. Una tensión de compresión es beneficiosa porque tiende a suprimir la ramificación de las grietas.
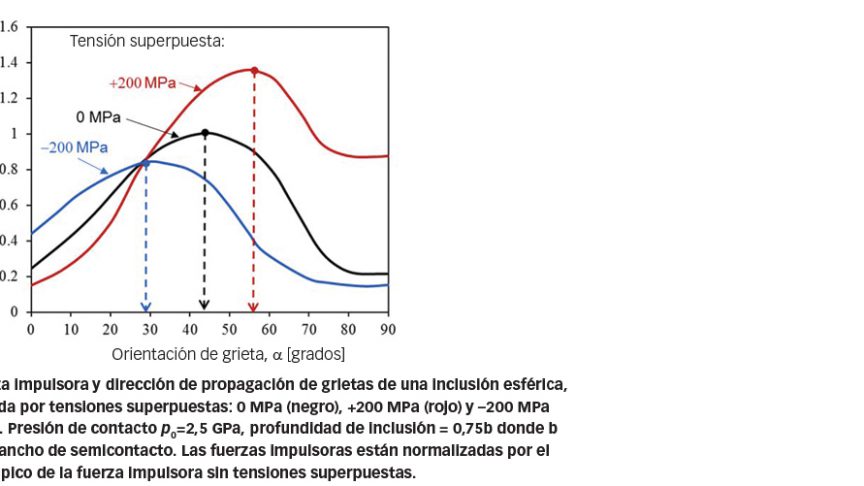
La fig. 7 muestra la fuerza que impulsa la propagación de grietas de una inclusión esférica como función de la orientación de la grieta, teniendo en cuenta una presión de contacto de 2,5 GPa y diferentes niveles de tensiones superpuestas. Se evaluaron las fuerzas impulsoras de grietas de diferente orientación. De la fig. 7 puede verse que, en ausencia de tensiones superpuestas, la fuerza impulsora máxima corresponde a una orientación de grieta de 45°. Si se aplica una tensión de compresión de 200 MPa, la curva de la fuerza impulsora alcanza su pico a un ángulo de 30°; sin embargo, si se aplica una tensión de tracción de 200 MPa, la orientación de la grieta en la cual la fuerza impulsora alcanza el valor máximo se incrementa a 57°. Puede decirse que una tensión de tracción puede acelerar la propagación de grietas y tiende a impulsar su crecimiento hacia un ángulo inclinado, mientras que una tensión de compresión puede retardar el crecimiento de grietas y tiende hacia una propagación de grietas en dirección horizontal.
Importancia desde la perspectiva de ingeniería
mos de fatiga ha conducido a que se identificara una de las causas raíz de fallas prematuras en los rodamientos [2]. La falla prematura de rodamientos caracterizada por grietas de corrosión blanca por ataque ácido (WEC) y grietas axiales se ha reproducido con éxito en pruebas en laboratorio. En ellas, el aro interior de un rodamiento de rodillos cilíndricos se había montado en un eje de manguito con ondulación introducida artificialmente. Quedó demostrado por simulación de FE que una desviación de forma del asiento de un rodamiento, ondulación por ejemplo, puede provocar tensiones de tracción cerca del camino de rodadura del aro interior. Si estas tensiones exceden de un determinado límite, pueden debilitar el material y, en combinación con tensión herciana, comportan una iniciación y crecimiento acelerado tempranos de grietas por imperfecciones preexistentes en el material, que desembocan en la falla prematura del rodamiento.
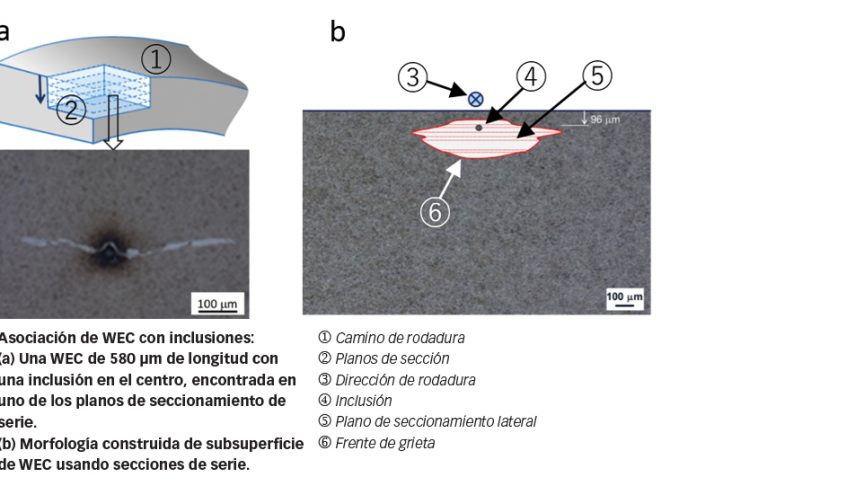
Además, la inspección metalográfica usando seccionamiento de serie de pequeños pasos de los aros sometidos a ensayos indicaba que las WEC que suelen encontrarse en rodamientos que fallan prematuramente pueden iniciarlas inclusiones subsuperficiales, tal como se indica en la fig. 8. Se llegó a una conclusión similar en una investigación independiente referida en [4]. La importancia de este hallazgo es la aclaración relativa al origen de las WEC. Puede decirse que una WEC es fundamentalmente una grieta subsuperficial, por ejemplo una mariposa, que puede iniciarse a partir de un incremento de tensiones, pero que ha crecido y llegado a una etapa avanzada. Un roce repetido entre superficies de grieta bajo RCF causa una alteración gradual de la microestructura que conduce a la formación de zonas blancas de corrosión ácida (WEA) cerca de las superficies de la grieta. Por ello, las WEC o WEA no son la causa de la falla prematura de los rodamientos, sino un síntoma de daños de RCF avanzados.
Resumen
La investigación de mecanismos de fatiga es fundamental para que el progreso de la tecnología de rodamientos aborde los retos de aplicaciones exigentes. El presente estudio demuestra que, al comprender mejor las imperfecciones del material y sus efectos sobre el rendimiento de los rodamientos, se esclarecen algunos problemas para los que pueden desarrollarse soluciones potenciales, a fin de reducir la tasa de fallas prematuras en los rodamientos. Además, pueden establecerse los límites de tolerancia para imperfecciones del material.
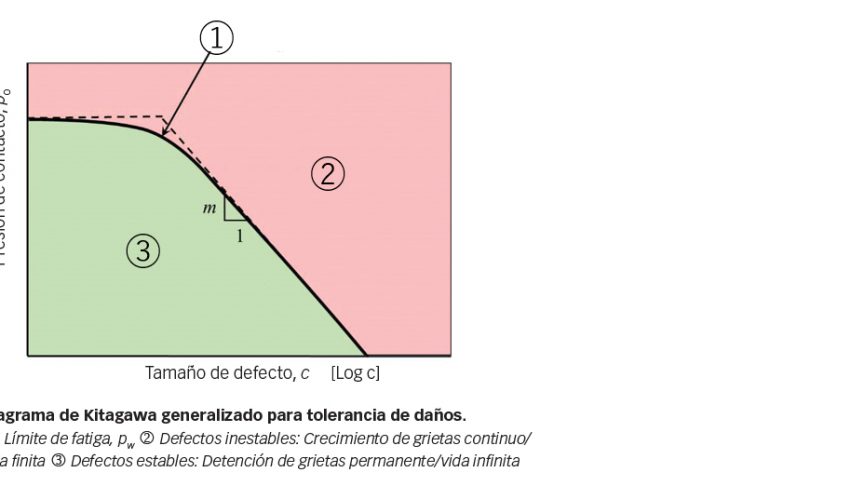
Los límites de tolerancia de imperfecciones del material pueden establecerse en virtud de un diagrama de Kitagawa generalizado, tal como se ilustra en la fig. 9, que relaciona, con respecto al tamaño del defecto, el límite de fatiga en términos de límite de presión de contacto máxima. Cuando el defecto es insignificante, la curva se acerca al límite de fatiga intrínseco del material matriz. En defectos grandes, el límite de fatiga puede determinarlo la condición umbral del comienzo del crecimiento de grieta por fatiga, es decir, la asíntota con una pendiente constante de –m, el valor de la cual depende del tipo de defecto.
Se propuso el diagrama de Kitagawa [6] original para los defectos similares a grietas en los que m = 0,5. El diagrama de Kitagawa generalizado puede aplicarse en diferentes materiales y defectos de diversos tipos. Por ejemplo, se ha usado para establecer el límite de tolerancia de los defectos del material que falta en la superficie de bolas de nitruro de silicio para rodamientos híbridos [6]. En este tipo de defecto, m es 0,46.
A partir de la descripción de iniciación y propagación de grietas por fatiga de inclusiones subsuperficiales, se ha desarrollado un modelo para predecir la resistencia a la fatiga a ciclos muy altos (very high cycle fatigue, VHCF) y el límite de fatiga de aceros de rodamientos. Se demostró [8] que hay una buena correlación entre los límites de fatiga pronosticados y los datos de pruebas de VHCF con el valor del límite de fatiga establecido en la norma ISO 281:2007 de la vida nominal de los rodamientos.
Referencias
[1] W. Solano-Alverez, H.K.D.H. Bhadeshia, White-etching matter in bearing steel. Part II: Distinguishing cause and effect in bearing steel failure, Metall. Mater. Trans. A 45A (2014) 4916-4931.
[2] J. Lai, K. Stadler, Investigation on the mechanisms of white etching crack (WEC) formation in rolling contact fatigue and identification of a root cause for bearing premature failure, Wear 364-365 (2016) 244-256.
[3] J.L. Johnson, Contact Mechanics, Cambridge University Press, 1985, Cambridge, UK.
[4] M. Evans, White structure flaking failure in bearings under rolling contact fatigue, PhD Thesis, University of Southampton, UK, 2013.
[5] H. Kitagawa, S. Takahashi, Applicability of fracture mechanics to small cracks or cracks in the early stage. In: Proceedings of the second international conference on mechanical behaviour of materials. ASM, 1976, pp. 627-631.
[6] J. Lai, Y. Kadin, C. Vieillard, Characterization and modelling of the degradation of silicon nitride balls with surface missing-material defects under lubricated rolling contact conditions, Wear 398-399 (2018) 146-157.
[7] J. Lai, T. Lund, K. Ryden, A. Gabelli, I. Strandell, The fatigue limit of bearing steels – Part I: A pragmatic approach to predict very high cycle fatigue strength, Int. J. Fatigue 38 (2012) 155-168.
[8] A. Gabelli, J. Lai, T. Lund, K. Rydén, I. Strandell, G.E. Morales-Espejel, The fatigue limit of bearing steels – Part II: Characterization for life rating standards, Int. J. Fatigue 38 (2012) 169-180.