Los engranajes están en contacto con elementos de máquinas que, en muchos aspectos, se enfrentan con retos muy similares a los de los rodamientos. También tienen importantes diferencias. En muchas aplicaciones, los rodamientos y engranajes trabajan conjuntamente y mantienen una estrecha interacción. Los ingenieros que trabajan con rodamientos, a menudo, se encuentran con la necesidad de tener conocimientos básicos de las condiciones de funcionamiento de los engranajes debido a que pueden influir en el comportamiento del rodamiento. Sin embargo, los métodos de cálculo de la vida útil son muy diferentes, a pesar de tener aspectos tribológicos similares. En este artículo, aspectos bien conocidos de la vida útil de la superficie del rodamiento se aplican a los engranajes, y se analiza el nuevo método de integración de superficie-subsuperficie para el cálculo de la vida útil del rodamiento, a fin de lograr una posible extensión a los engranajes. De este modo, por primera vez, el cálculo de los rodamientos y engranajes podría hacerse con exactamente la misma metodología.

Las condiciones tribológicas de las superficies de los flancos de los dientes del engranaje son similares a las condiciones de las superficies de contacto de los rodamientos, aunque diferentes en magnitud. En ambos tipos de superficie, hay rodadura/deslizamiento (en los rodamientos, mucho menor deslizamiento que en los engranajes), ambos sufren presiones elevadas (los rodamientos, más elevadas que los engranajes) y ambos tienen rugosidad superficial de una magnitud del mismo orden que el espesor de película lubricante. Todo esto apunta hacia la posibilidad de que puedan aplicarse métodos de cálculo de la vida útil de las superficies de contacto de los engranajes similares a los aplicados a las superficies de los rodamientos. Un buen ejemplo de ello es el modelo de deformación superficial de SKF [1], desarrollado originalmente para los rodamientos y aplicado más tarde a los engranajes [2].

Hoy, la vida nominal de los engranajes y rodamientos se calcula de formas diferentes. La selección y los métodos de diseño de los engranajes se basan, en general, en la ecuación de Lewis [3] para la flexión de vigas. El estándar de la AGMA [4] introduce factores de seguridad adicionales a la ecuación de Lewis para tener en cuenta la concentración de tensiones en la raíz del diente, la distribución de la carga y la sobrecarga en el diente. Además de la resistencia a la fatiga de la raíz del diente, la AGMA también incluye la verificación de la condición de tensión máxima desarrollada en la superficie de contacto del diente.

La AGMA introduce una ecuación para la durabilidad de la superficie basada en tensiones de contacto “secas”, de modo que, cuando la tensión de contacto supera un determinado valor crítico, se considera que el diente de engranaje se desconchará. Estos métodos se han usado con éxito en el diseño y dimensionado de los engranajes durante las últimas décadas. No obstante, con el incremento de las demandas de la industria de reducir el tamaño de los componentes de las máquinas, y de disminuir el consumo de energía y los costos de fabricación, los ingenieros están buscando constantemente nuevas maneras de optimizar las dimensiones de los componentes mecánicos.

Los últimos conocimientos tribológicos en lubricación automática, acabado superficial avanzado y control de limpieza pueden contribuir claramente a la durabilidad de los engranajes. Esto puede brindar nuevas oportunidades de reducir el sobrediseño e incrementar la eficiencia mecánica. Hoy, en las organizaciones de estandarización de los engranajes, se están haciendo esfuerzos considerables para determinar en ellos el riesgo de microdesconchado (micropicado) [5], lo que indica la importancia de esta cuestión en cuanto a su durabilidad. Sin embargo, hasta ahora, los aspectos tribológicos (denominados riesgo de microdesconchado) solo pueden considerarse indirectamente en el proceso de diseño del engranaje y, contrariamente al enfoque usado en los rodamientos, no hay directrices específicas respecto de la longevidad del engranaje.

En cambio, a lo largo de los años, los rodamientos han aprovechado los aspectos de modelización especializados y únicos en su clase para predecir la vida a fatiga esperada del contacto rodante con respecto a las condiciones de funcionamiento. Los más significativos son:

• la aplicación de la teoría de Weibull del eslabón más débil de la resistencia del material [6], que tiene en cuenta el volumen de tensión del material en riesgo
• el uso de la teoría de la capacidad de carga dinámica de Lundberg-Palmgren [7-8]
• el enfoque estadístico de la definición de resistencia a la fatiga, es decir, un 90% de confiabilidad de la vida útil L₁₀
• la aplicación del criterio de tensiones de fatiga de Ioannides-Harris [9], que permite incluir el efecto de la calidad de la lubricación y la limpieza en la vida a fatiga del contacto rodante.

Además, muy recientemente se introdujo un nuevo enfoque general sobre la vida a fatiga de un contacto rodante, el denominado Modelo generalizado de cálculo de vida útil de rodamientos (Generalized Bearing Life Model, GBLM) [artículo en Evolution #4-2015 de SKF]. En este nuevo método, los daños originados en la superficie se formulan explícitamente en las ecuaciones de fatiga básica del contacto rodante. El método toma en consideración la probabilidad de supervivencia de la superficie como un riesgo de falla que se separa de las tensiones hercianas de la subsuperficie [10-11]. Esto abre nuevas posibilidades en el uso de modelos tribológicos especializados para describir las fallas del contacto rodante relacionadas con la superficie.

Los engranajes todavía no han aprovechado esos conceptos de modelización. Ni el uso de L₁₀ ni el de la capacidad de carga dinámica han prosperado en el diseño de engranajes, a pesar de los esfuerzos significativos realizados durante la década del setenta por la labor pionera de Coy et al. [12-15].

El objetivo aquí es comentar brevemente una adaptación del modelo [10] y estudiar su aplicación potencial a los engranajes. El concepto principal se describe en la fig. 1. Las zonas de tensiones en la superficie y subsuperficie del contacto del engranaje se analizan separadamente en cuanto a su contribución a la supervivencia del dentado del engranaje, aunque ambas se han incluido en la estimación de L₁₀.

Esto será útil para ilustrar las ventajas del método de vida nominal propuesto en comparación con los actuales, y presentará las posibilidades ofrecidas por el uso de un enfoque más integrado de la vida de útil de las superficies de contacto de los engranajes.

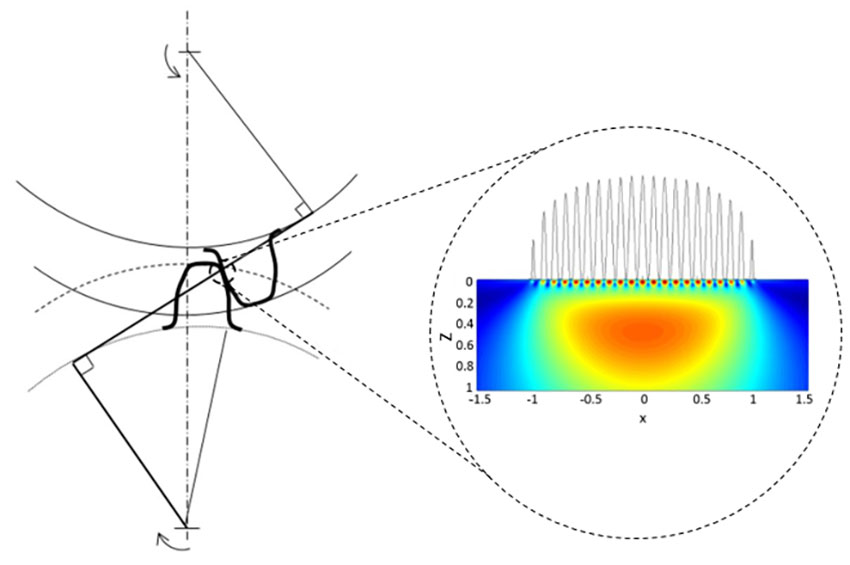
Condiciones tribológicas de los rodamientos y engranajes

La fig. 2 muestra una comparación entre las condiciones tribológicas típicas de los engranajes y rodamientos. Puede verse que, en general, las condiciones de un rodamiento parecen ser más exigentes que las de los engranajes, con mayores presiones, una vida útil requerida más larga y menores espesores de película lubricante. Sin embargo, los engranajes muestran un mayor deslizamiento y una rugosidad más alta, lo que no favorece la vida útil de las superficies. Además, los engranajes tienden a tener una configuración de superficie transversal al sentido de rodadura/deslizamiento, al contrario de los rodamientos, que, en general, tienen una configuración de rugosidad a lo largo del sentido de rodadura. Esto, en condiciones de lubricación mixta, puede ser una ventaja para los rodamientos.

La vida útil de una superficie tribológica en los engranajes y rodamientos la determinan principalmente dos factores importantes: la calidad de la lubricación y la contaminación sólida, dos aspectos considerados en el cálculo general de la vida útil del rodamiento (ISO 281), pero no considerados plenamente en el cálculo actual de la vida útil del engranaje. No obstante, el concepto recientemente desarrollado de introducir la probabilidad de supervivencia de la superficie como un riesgo de falla separado de las tensiones hercianas de la subsuperficie (el GBLM) podría ayudar a considerar los mismos aspectos de la superficie en engranajes que en rodamientos, y de una vez por todas unificar los métodos de cálculo.

Deformación superficial en engranajes

Los engranajes, al igual que los rodamientos, pueden estar expuestos a deformación superficial (también denominada microdesconchado o coloración gris) si las condiciones de lubricación no son adecuadas. Esto puede suceder en condiciones de viscosidad de aceite baja, rugosidad excesiva en los engranajes, y condiciones de velocidad baja. En otras palabras, a una calidad de lubricación baja o relación baja.

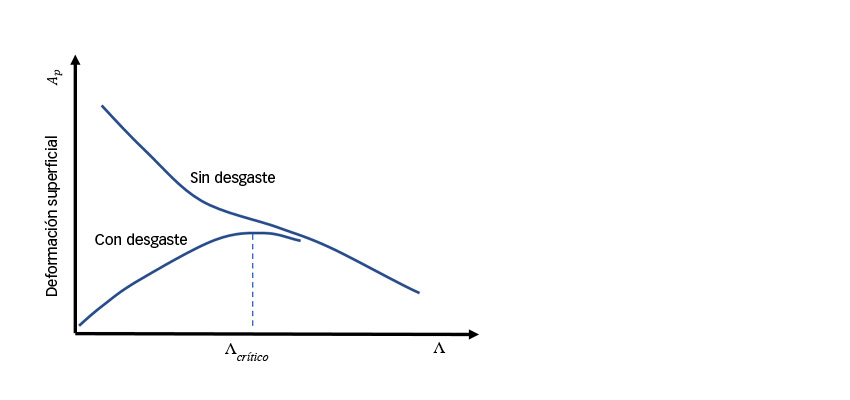
La deformación superficial es el resultado de fatiga de la superficie a nivel de la aspereza compitiendo con un desgaste leve [1–2]. Un desgaste leve puede eliminar los picos de aspereza y reducir las presiones locales, y así disminuir las tensiones en la superficie y la fatiga. Un desgaste leve también puede eliminar las capas de material fatigado. Demasiado poco desgaste leve puede prolongar la fase de rodaje de las superficies, y así generar más daños y causar más deformación superficial. En esta condición, valores más bajos pueden llevar a menor deformación superficial debido a que el desgaste aumentará; de lo contrario, aumentaría la deformación superficial. Esto se ilustra en la fig. 3.

Otro aspecto importante de la deformación superficial en los engranajes es el caso de lo que se denomina condiciones de deslizamiento negativo, cuando se observa la superficie más lenta. Se dice con frecuencia que esta superficie más lenta es más propensa a verse afectada por deformación superficial que la superficie más rápida. Este fenómeno se explica en [2], donde se muestra que una superficie más lenta sufrirá más microciclos de fatiga producidos por la rugosidad de la superficie más rápida, además de los efectos potenciales de apertura y propagación más rápida de grietas superficiales.

Vida útil de engranaje con supervivencia de la superficie y subsuperficie

En [16] se ofrecen detalles completos del modelo propuesto; sin embargo, aquí es importante citar la ecuación de la vida útil final

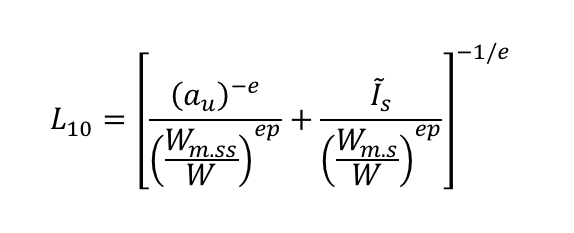
En donde:

Esta ecuación de la vida útil (1) tiene dos términos, el primero (lado izquierdo) solo se refiere a la subsuperficie, donde pueden aplicarse ecuaciones de Hertz clásicas. El segundo término (lado derecho) solo se refiere a los términos de superficie, donde se usan modelos tribológicos más sofisticados [1] para calcular el daño superficial. Esta ecuación sigue el mismo concepto que el GBLM desarrollado para rodamientos.

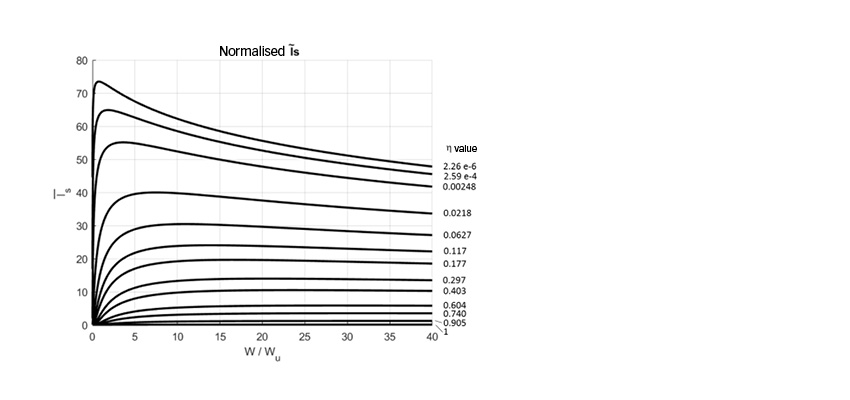
Anteriormente las ecuaciones de la capacidad de carga dinámica de los engranajes (subsuperficie) W_m.ss se han presentado con la labor de Coy et al. [12-15]. En [16] se introduce una ecuación de la capacidad de carga dinámica (superficie) W_m.s. Obsérvese que, a diferencia de los rodamientos, aquí también se introduce una capacidad de carga dinámica de la superficie. En rodamientos, sería equivalente a introducir también un valor “C” para la superficie.

Fig. 4. Ejemplo de valor Ĩ_s normalizado, usado en los ejemplos, con η como factor medioambiental η=η_b η_c (como en los rodamientos).

Caso de aplicación

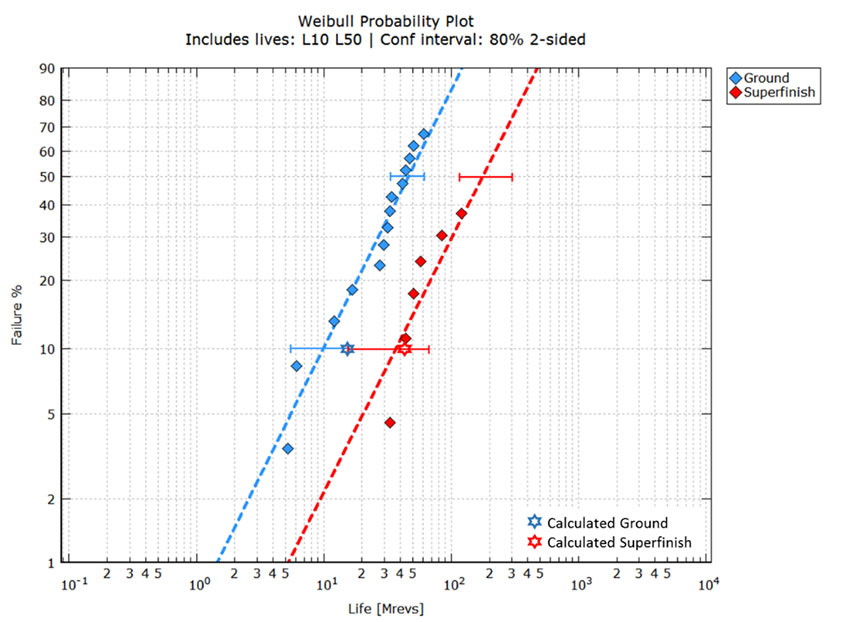
La referencia [17] compara la vida útil de dos conjuntos de engranajes rectos, uno con las superficies solo rectificadas y el otro con las superficies superpulidas. Todos los datos de los engranajes, materiales, geometría y condiciones de funcionamiento se presentan en la referencia. Los dos conjuntos se han probado con las mismas condiciones de funcionamiento, excepto en que el conjunto con las superficies rectificadas empeora con una relación más baja debido a su mayor rugosidad ( 1,13), y el conjunto con las superficies superpulidas muestra una mejor calidad de la lubricación debido a su menor rugosidad ( 6,17). Los datos de la prueba presentados en [17] de los engranajes rectificados y superpulidos se han digitalizado y presentado en el gráfico en la fig. 5, que muestra una comparación de los datos medidos y calculados.

La fig. 5 muestra que los intervalos de confianza se superponen ligeramente y se precisarían más fallas (especialmente en la versión superpulida) para reducir la incertidumbre. En cualquier caso, de los datos se desprende una clara diferenciación en la vida útil. Esta figura también muestra las vidas útiles calculadas con la aplicación de la ecuación (1) (asteriscos).

Las vidas útiles calculadas sobreestiman ligeramente las mediciones, algo más en la versión rectificada que en la superpulida. Con la disponibilidad de pruebas posteriores, el modelo podría calibrarse mejor siguiendo los métodos ya usados para los rodamientos. Sin embargo, en esta etapa, el objetivo principal es dar una primera evaluación de la teoría básica sin la interferencia de los factores de calibración. Teniendo esto en cuenta, tal como se muestra en la fig. 5, la comparación entre los datos de la prueba y los resultados calculados usando la metodología presentada aquí muestra una buena correlación.

Conclusiones

Ahora se ha adaptado a los engranajes un modelo de concepto de supervivencia de la superficie y subsuperficie por fatiga de contacto rodante inicialmente desarrollado para rodamientos. Como ejemplo de aplicación, se ha mostrado el efecto de la calidad de la lubricación.

El modelo de concepto puede desarrollarse hasta un modelo predictivo una vez calibrado con el uso de resultados más experimentales en engranajes, realizados en diferentes condiciones de aplicación. Es necesario tener especialmente en cuenta el efecto del material, la lubricación, el acabado superficial y la contaminación de partículas.

No obstante, incluso en el estado de concepto, el modelo ya puede dar valores correctos de referencias [12–15, 17] en pruebas con engranajes rectos. Por primera vez, un modelo de vida útil de engranaje muestra un parámetro nominal de la superficie (capacidad de carga dinámica de la superficie).

De las observaciones aquí presentadas, pueden extraerse las siguientes conclusiones:

1. El enfoque actual introduce una separación de la supervivencia de la superficie y la subsuperficie. Por tanto, podrían obtenerse ventajas significativas incrementando la flexibilidad en la modelización de la vida útil de los engranajes puesto que se analiza más de una región. Esto permitiría a los ingenieros introducir modos de falla de la superficie además de la fatiga herciana por contacto rodante.
2. Debido a que los efectos de la superficie se incorporan directamente en la formulación, este enfoque permite aprovechar los conocimientos obtenidos del uso de modelos tribológicos avanzados. En el futuro, podrían incluirse efectos no tribológicos, como tensiones de raíz del diente.
3. La introducción en los engranajes de la capacidad de soportar cargas dinámicas en la superficie, además de la capacidad de soportarlas en la subsuperficie, es una innovación que podría dar flexibilidad en la clasificación de engranajes de características especiales que influyen claramente en el rendimiento de la superficie, como tratamientos superficiales, revestimientos y acabado.
4. Especialmente en el diseño de cajas de engranaje, una homologación de los métodos de cálculo de la vida útil entre engranajes y rodamientos sería extremadamente útil, no solo al considerar suposiciones iguales en rodamientos y engranajes, sino también confiabilidades comunes.