Bei Zahnrädern handelt es sich um formschlüssige Maschinenelemente, die in vielerlei Hinsicht ähnliche Anforderungen wie Wälzlager erfüllen müssen, sich aber auch erheblich von diesen unterscheiden. In vielen Anwendungen sind Wälzlager und Zahnräder gemeinsam im Einsatz und stehen in enger Wechselbeziehung zueinander. Ingenieure, die sich mit Wälzlagern befassen, müssen oft auch ein grundlegendes Verständnis für die Betriebsbedingungen von Zahnrädern haben, da diese das Lagerverhalten beeinflussen können. Trotz ähnlicher tribologischer Aspekte unterscheiden sich die Lebensdauerberechnungsmethoden jedoch sehr voneinander. In diesem Artikel werden die bei Wälzlagern bekannten Aspekte zur Oberflächenlebensdauer auf Zahnräder angewendet. Die neue Methode zur Berücksichtigung von Werkstoffermüdung an und unterhalb der Oberfläche in der Lebensdauerberechnung wird im Hinblick auf eine mögliche Ausweitung auf Zahnräder untersucht. So könnte es erstmals möglich sein, Wälzlager und Zahnräder mit genau derselben Methodik zu berechnen.

Die tribologischen Verhältnisse der Zahnflankenoberflächen von Zahnrädern sind ähnlich wie die der Kontaktflächen von Wälzlagern, aber sie unterscheiden sich in ihrer Größenordnung. Auf beiden Arten von Oberflächen gibt es Roll-/Gleitvorgänge (bei Wälzlagern viel geringere Gleitvorgänge als bei Zahnrädern), beide verfügen über hohe Flächenpressungen (bei Wälzlagern höhere als bei Zahnrädern) und beide weisen eine Oberflächenrauheit in der gleichen Größenordnung wie die Schmierfilmdicke auf. All dies deutet auf die Möglichkeit hin, dass zur Berechnung der Oberflächenlebensdauer von Zahnradkontaktflächen ähnliche Methoden wie bei Wälzlageroberflächen angewendet werden können. Ein gutes Beispiel dafür ist das SKF Modell für Oberflächenzerrüttung [1], das ursprünglich für Wälzlager entwickelt wurde und jetzt auch bei Zahnrädern [2] angewendet werden soll.

Die Lebensdauerberechnung von Zahnrädern und Wälzlagern wird heute auf unterschiedliche Weise durchgeführt. Bei der Auswahl und Konstruktion von Zahnrädern wird im Allgemeinen die Lewis-Gleichung [3] für Balkenbiegung zugrunde gelegt. In der AGMA-Norm [4] wurden zusätzliche Sicherheitsfaktoren in die Lewis-Gleichung aufgenommen, um die Spannungskonzentration im Zahnfuß sowie die Überlast und die Lastverteilung auf den einzelnen Zahn zu berücksichtigen. Zusätzlich zur Ermüdungsfestigkeit des Zahnfußes sieht AGMA auch die Überprüfung des maximalen Spannungszustandes vor, der an der Oberfläche des Zahnkontaktes entsteht.

AGMA führte eine Gleichung für die Oberflächenbeständigkeit ein, die auf „trockenen“ Kontaktspannungen basiert, so dass berücksichtigt wird, dass Ausbrüche an den Verzahnungen entstehen, sobald die Kontaktspannung einen bestimmten kritischen Wert überschreitet. Diese Methoden wurden in den letzten Jahrzehnten erfolgreich zur Auslegung und Dimensionierung von Zahnrädern eingesetzt. Angesichts der verstärkten Forderungen der Industrie nach Downsizing und einer Senkung des Energieverbrauchs sowie der Herstellungskosten sind Ingenieure jedoch ständig auf der Suche nach moderneren Möglichkeiten zur Optimierung der Abmessungen mechanischer Komponenten.

Die neuesten tribologischen Erkenntnisse in den Bereichen automatisierte Schmiersysteme, verbesserte Oberflächenbeschaffenheit und Überwachung der Reinheit können erheblich zur Langlebigkeit von Zahnrädern beitragen. Dies kann neue Möglichkeiten zur Vermeidung von Überdimensionierung und zur Steigerung des mechanischen Wirkungsgrades eröffnen. Heute werden innerhalb der Normungsorganisationen für Zahnräder beträchtliche Anstrengungen unternommen, um das Risiko von Mikroausbrüchen (Micropitting) bei Zahnrädern zu bewerten [5]. Dies weist auf die Bedeutung dieses Themas im Hinblick auf die Lebensdauer von Zahnrädern hin. Allerdings können tribologische Aspekte wie das Risiko von Mikroausbrüchen bisher nur indirekt bei der Konstruktion von Zahnrädern berücksichtigt werden. Anders als bei Wälzlagern, gibt es keine speziellen Richtlinien hinsichtlich der voraussichtlichen Lebensdauer von Zahnrädern.

Im Gegensatz dazu haben sich bei Wälzlagern im Laufe der Jahre besonders spezialisierte Methoden für die Vorhersage der zu erwartenden Ermüdungslebensdauer von Wälzkontakten unter den jeweiligen Betriebsbedingungen als nützlich erwiesen. Die wichtigsten sind:

• die Anwendung von Weibulls Theorie des schwächsten Glieds hinsichtlich der Werkstofffestigkeit [6], die das gefährdete Spannungsvolumen des Werkstoffs berücksichtigt
• die Anwendung der von Lundberg und Palmgren entwickelten Theorie der dynamischen Tragzahl [7-8]
• der statistische Ansatz bei der Definition der Ermüdungslebensdauer, d. h. 90 %ige Erlebenswahrscheinlichkeit bei der nominellen Lebensdauer L₁₀
• die Anwendung des Kriteriums der Ermüdungstheorie nach Ioannides und Harris [9], mit dem der Einfluss des Schmierfilmaufbaus und der Schmierstoffreinheit auf die Ermüdungslebensdauer von Wälzkontakten berücksichtigt werden kann.

Darüber hinaus wurde vor kurzem ein neuer allgemeiner Ansatz zur Bestimmung der Ermüdungslebensdauer von Wälzkontakten eingeführt. Dabei handelt es sich um das so genannte Generalized Bearing Life Model oder GBLM [SKF Evolution #4 2015, S. 21ff.]. Bei dieser neuen Methode wird der von der Oberfläche ausgehende Schaden explizit in den grundlegenden Ermüdungsgleichungen des Wälzkontakts formuliert. So wird die Erlebenswahrscheinlichkeit der Oberfläche als Versagensrisiko betrachtet, das von den Hertz’schen Spannungen unterhalb der Oberfläche getrennt ist [10-11]. Dies eröffnet neue Möglichkeiten für den Einsatz von spezialisierten Tribologiemodellen zur Beschreibung von oberflächenbedingten Wälzkontaktausfällen.

Zahnräder haben bisher noch nicht von diesen Modellansätzen profitiert. Trotz erheblicher Anstrengungen in den 1970er-Jahren durch die Pionierarbeit von Coy und anderen [12-15] hat sich in der Zahnradkonstruktion weder die Anwendung von L10 noch die der dynamischen Tragzahl wirklich durchgesetzt.

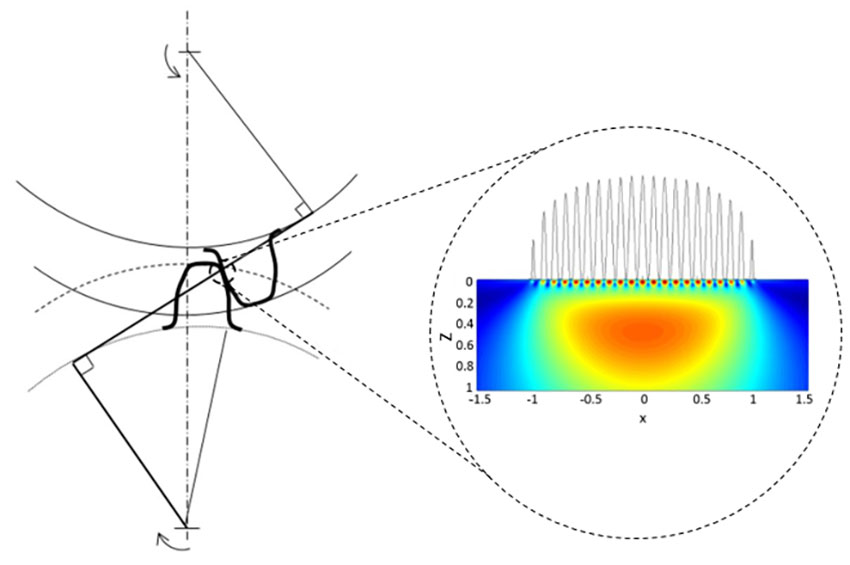
Im Folgenden soll eine Anpassung des Modells [10] andiskutiert und seine mögliche Anwendung bei Zahnrädern untersucht werden. In Bild 1 ist das Grundkonzept dargestellt. Die Spannungsbereiche an und unterhalb der Oberfläche des Zahnradkontakts werden hinsichtlich ihres Beitrags zur Standfestigkeit der Verzahnung getrennt analysiert; beide Bereiche werden aber in die Bestimmung von L₁₀ einbezogen.

So lassen sich die Vorteile der vorgeschlagenen Lebensdauerberechnungsmethode im Vergleich zu den derzeit verwendeten Methoden besser darstellen. Ferner werden Möglichkeiten aufgezeigt, die sich durch die Verwendung eines integrierteren Ansatzes für die Lebensdauerberechnung der Kontaktflächen von Zahnrädern ergeben.

Tribologische Bedingungen bei Wälzlagern und Zahnrädern

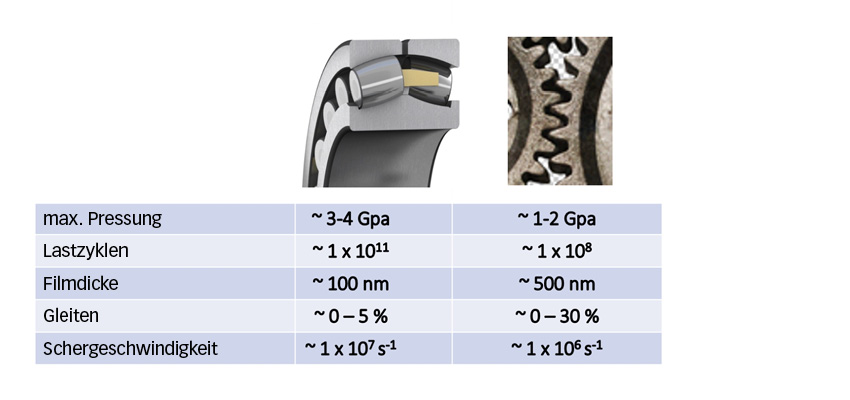
Bild 2 zeigt einen Vergleich zwischen Zahnrädern und Wälzlagern unter typischen tribologischen Bedingungen. Man kann erkennen, dass die Bedingungen in einem Wälzlager im Allgemeinen anspruchsvoller zu sein scheinen als bei Zahnrädern, und zwar mit höheren Pressungen, längeren Gebrauchsdauern und dünneren Schmierfilmdicken. Zahnräder weisen jedoch mehr Gleitbewegungen und eine höhere Rauheit auf, was sich nicht günstig auf die Lebensdauer der Oberflächen auswirkt. Außerdem haben Zahnräder tendenziell eine quer zur Roll-/Gleitrichtung ausgerichtete Oberfläche; im Gegensatz dazu ist die Rauheit von Wälzlagern häufig in Rollrichtung ausgerichtet. Dies kann bei Mischreibung ein Vorteil für Wälzlager sein.

Die Lebensdauer einer tribologischen Oberfläche bei Zahnrädern und Wälzlagern wird hauptsächlich von zwei wichtigen Faktoren bestimmt: dem Schmierfilmaufbau und der Schmierstoffverunreinigung. Beide Aspekte werden zwar bei der Gesamtberechnung der Wälzlagerlebensdauer (ISO 281) berücksichtigt, aber in die derzeitige Lebensdauerberechnung von Zahnrädern werden sie nicht vollständig einbezogen. Das kürzlich entwickelte Konzept, die Erlebenswahrscheinlichkeit der Oberfläche als Versagensrisiko getrennt von den Hertz’schen Spannungen unterhalb der Oberfläche einzuführen (GBLM), könnte jedoch bewirken, dass bei Zahnrädern die gleichen Oberflächenaspekte wie bei Wälzlagern Berücksichtigung finden und die Berechnungsmethoden endlich vereinheitlicht werden.

Oberflächenzerrüttung bei Zahnrädern

Bei Zahnrädern wie auch bei Wälzlagern könnte bei nicht ausreichenden Schmierbedingungen Oberflächenzerrüttung (auch Graufleckigkeit genannt) auftreten. Dies kann beim Einsatz niedrig viskoser Öle, bei Zahnrädern mit zu hohen Rauheitswerten und bei potenziell niedrigen Drehzahlen geschehen. Das heißt, wenn unzureichende Schmierbedingungen vorliegen oder das Λ-Verhältnis niedrig ist.

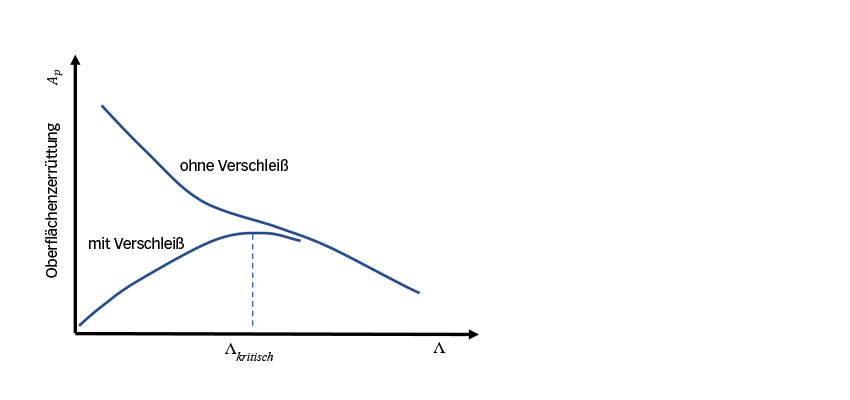
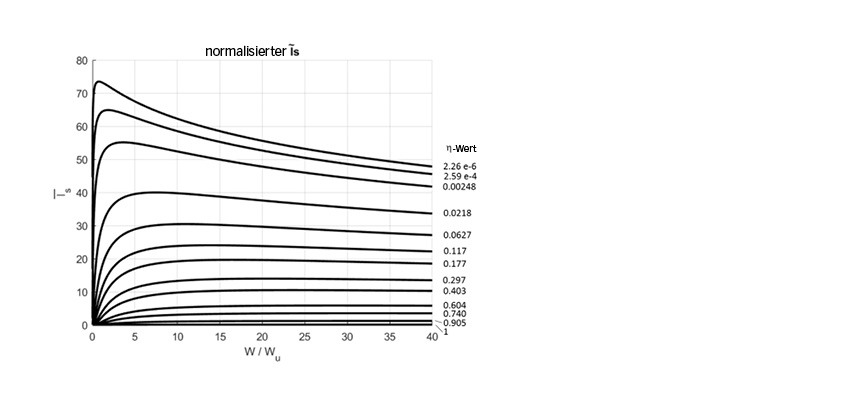
Oberflächenzerrüttung ist das Ergebnis einer Oberflächenermüdung im Bereich der Rauheitsspitzen. Sie konkurriert mit mildem Verschleiß [1-2]. Ein ausreichend milder Verschleiß könnte die Rauheitsspitzen beseitigen und kann die lokalen Pressungen senken, was zu niedrigeren Oberflächenspannungen und einer geringeren Ermüdung führt. Milder Verschleiß könnte auch die ermüdeten Materialschichten abtragen. Ein zu geringer milder Verschleiß könnte die Einlaufphase der Oberflächen verzögern, ein erhöhtes Schadensniveau bewirken und eine stärkere Oberflächenzerrüttung verursachen. In diesem Fall könnten niedrigere Λ-Werte zu einer geringeren Oberflächenzerrüttung führen, da der Verschleiß zunimmt; ansonsten sollte die Oberflächenzerrüttung zunehmen. Dies ist in Bild 3 dargestellt.

Ein weiterer wichtiger Aspekt der Oberflächenzerrüttung bei Zahnrädern zeigt sich im Falle der so genannten negativen Gleitbedingungen bei Betrachtung der langsameren Oberfläche. Häufig spricht man davon, dass die langsamere Oberfläche anfälliger für Oberflächenzerrüttung ist als die schnellere. Dieses Phänomen wurde in [2] erläutert. Hervorgerufen durch die Rauheit der schnelleren Oberfläche treten auf der langsameren mehr Mikroermüdungszyklen auf, und zwar neben den potenziellen Auswirkungen von sich öffnenden Oberflächenrissen und deren schnellerer Ausbreitung.

Lebensdauer von Zahnrädern mit Erlebenswahrscheinlichkeit der Bereiche an und unterhalb der Oberfläche

Sämtliche Angaben zum vorgeschlagenen Modell sind in [16] enthalten; hier ist es jedoch wichtig, die endgültige Lebensdauergleichung anzugeben.

 

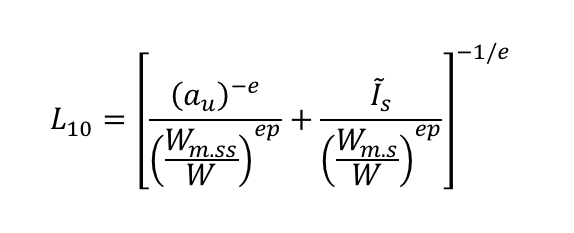
Diese Lebensdauergleichung (1) beinhaltet zwei Hauptterme: Der erste Term (links) bezieht sich nur auf den Bereich unterhalb der Oberfläche, auf den die klassischen Hertz’schen Gleichungen angewendet werden können. Der zweite Term (rechts) bezieht sich nur auf die Bedingungen an der Oberfläche, wo komplexere tribologische Modelle [1] zur Bestimmung der Oberflächenschäden verwendet werden. Diese Gleichung ist nach dem gleichen Konzept aufgebaut wie das für Wälzlager entwickelte GBLM.

In der Vergangenheit wurden Gleichungen für die dynamische Tragfähigkeit von Zahnrädern W_m.ss (Bereich unter der Oberfläche) von Coy und anderen Wissenschaftlern [12-15] aufgestellt. Eine Gleichung für die dynamische Tragfähigkeit W_m.s (Bereich an der Oberfläche) wird in Referenz [16] vorgestellt. Zu beachten ist, dass hier, anders als bei Wälzlagern, auch eine dynamische Tragfähigkeit für den Bereich an der Oberfläche eingeführt wird. Bei Wälzlagern entspräche dies der Einführung eines „C“-Wertes auch für den Bereich an der Oberfläche.

Bild 4: Beispiel des normalisierten Ĩ_s-Wertes, wie er in den Beispielen verwendet wird, wobei η für den Umgebungsfaktor η=η_b η_c (wie bei Wälzlagern) steht.

Anwendungsfall

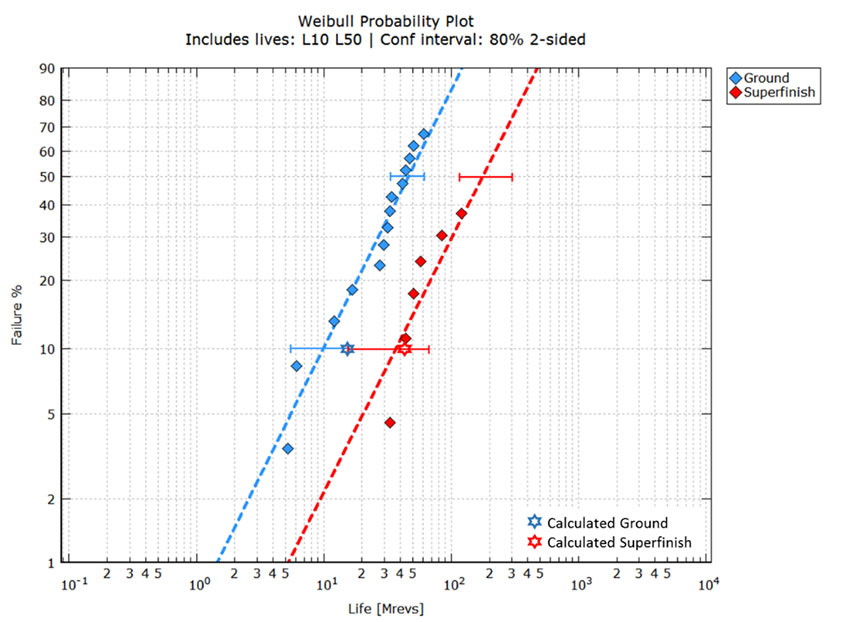
In Referenz [17] werden die Lebensdauern von zwei Geradzahnradpopulationen verglichen, von denen die eine nur geschliffene Oberflächen und die andere mit dem Superfinish-Verfahren bearbeitete Oberflächen aufweist. Sämtliche Zahnraddaten, Werkstoffe, Geometrieangaben und Betriebsbedingungen werden in der Referenz genannt. Die beiden Populationen wurden unter den gleichen Betriebsbedingungen getestet, mit dem Unterschied, dass die Population mit der geschliffenen Oberfläche bei einem niedrigeren Λ-Verhältnis aufgrund ihrer höheren Rauheitswerte (Λ≈1,13) einen schlechteren Schmierfilmaufbau aufweist. Während sich die Population mit der mit dem Superfinish-Verfahren bearbeiteten Oberfläche aufgrund ihrer niedrigeren Rauheitswerte durch einen besseren Schmierfilmaufbau auszeichnet (Λ≈6,17). Die in Referenz [17] vorgestellten Testdaten für die geschliffenen Zahnräder und für die mit dem Superfinish-Verfahren bearbeiteten Zahnräder wurden digitalisiert und in Bild 5 neu dargestellt, wobei ein grafischer Vergleich der gemessenen und berechneten Daten vorgenommen wurde.

Bild 5 zeigt, dass sich die Vertrauensbereiche etwas überschneiden und mehr Ausfälle erforderlich wären (insbesondere bei der mit dem Superfinish-Verfahren bearbeiteten Variante), um die Unsicherheit zu verringern. Anhand der Daten lässt sich in jedem Fall ein deutlicher Unterschied hinsichtlich der Lebensdauern feststellen. Dieses Bild zeigt auch die berechneten Lebensdauern bei Anwendung von Gleichung (1) (Sterne).

Die berechneten Lebensdauern liegen leicht über den Messungen, etwas mehr bei der geschliffenen Variante als bei der mit dem Superfinish-Verfahren bearbeiteten Variante. Sobald weitere Tests verfügbar sind, könnte das Modell besser nach den bereits bei Wälzlagern angewendeten Methoden ausgerichtet werden. In dieser Phase besteht das Hauptziel jedoch darin, eine erste Bewertung der grundlegenden Theorie ohne den Einfluss von Anpassungsfaktoren vorzunehmen. Unter diesem Gesichtspunkt zeigt der in Bild 5 dargestellte Vergleich zwischen den Testdaten und den mit der hier vorgestellten Methode berechneten Ergebnissen eine sehr gute Korrelation.

Schlussfolgerungen

Ein ursprünglich für Wälzlager entwickeltes Konzept für Erlebenswahrscheinlichkeiten bei Wälzermüdung an und unterhalb der Oberfläche wurde nun für Zahnräder angepasst. Als Anwendungsbeispiel wurde der Einfluss des Schmierfilmaufbaus aufgezeigt.

Das Konzept kann zu einem Vorhersagemodell werden, sobald es unter Verwendung von weiteren experimentellen Ergebnissen angepasst wurde, die anhand von Zahnrädern unter verschiedenen Einsatzbedingungen ermittelt werden. Dabei müssen insbesondere die Einflüsse von Material, Schmierung, Oberflächenbeschaffenheit und Partikelverunreinigung berücksichtigt werden.

Das Modell kann aber auch im Konzeptstadium bereits die richtigen Werte für Tests mit Geradzahnrädern aus den Referenzen [12-15, 17] liefern. Zum ersten Mal weist ein Zahnrad-Lebensdauermodell einen Bemessungsparameter für die Oberfläche auf (dynamische Tragfähigkeit der Oberfläche).

Aus der hier vorgestellten Analyse lassen sich folgende Schlussfolgerungen ziehen:

1. Der derzeitige Ansatz sieht eine Trennung der Erlebenswahrscheinlichkeiten an und unterhalb der Oberfläche vor. Durch die Analyse von mehr als einem Bereich könnten sich erhebliche Verbesserungen aufgrund einer erhöhten Flexibilität in der Lebensdauermodellierung von Zahnrädern ergeben. Ingenieure haben die Möglichkeit oberflächeninduzierte Schadensmechanismen, zusätzlich zur Wälzermüdung infolge Hertz’scher Pressung einzubeziehen.
2. Da die Oberflächeneffekte direkt in die Formulierung einfließen, ermöglicht dieser Ansatz die Nutzung von Erkenntnissen, die durch die Verwendung erweiterter tribologischer Modelle gewonnen wurden. Nicht tribologische Effekte, wie beispielsweise Zahnfußspannungen, könnten in Zukunft einbezogen werden.
3. Die Einführung einer dynamischen Tragfähigkeit der Oberfläche zusätzlich zur dynamischen Tragfähigkeit des Bereichs unterhalb der Oberfläche bei Zahnrädern ist eine Innovation, die Flexibilität in die Auslegung von Zahnrädern mit speziellen Oberflächeneigenschaften zur Verbesserung der Leistungsfähigkeit bringen würde, wie zum Beispiel Oberflächenbehandlungen, -beschichtungen und -bearbeitungen.
4. Insbesondere bei der Konstruktion von Getrieben wäre eine Homologation der Lebensdauerberechnungsmethoden von Zahnrädern und Wälzlagern äußerst nützlich, und zwar nicht nur hinsichtlich gleicher Annahmen für Wälzlager und Zahnräder, sondern auch im Hinblick auf eine einheitliche Zuverlässigkeit.