Gli ingranaggi sono elementi di contatto delle macchine, che, sotto molti aspetti, affrontano problemi analoghi ai cuscinetti volventi. Si differenziano però anche in modo notevole. In molte applicazioni cuscinetti volventi e ingranaggi operano insieme e interagiscono strettamente. Gli ingegneri che lavorano con i cuscinetti volventi spesso devono possedere alcune conoscenze di base sulle condizioni di esercizio degli ingranaggi, perché possono influire sul comportamento dei cuscinetti. Tuttavia, anche se gli aspetti tribologici sono simili, i metodi per calcolare la durata sono molto diversi. In questo articolo si adottano per gli ingranaggi aspetti relativi alla durata superficiale ben noti nei cuscinetti e si analizza il nuovo metodo dell’integrazione degli effetti della fatica superficiale e sub-superficiale per una sua eventuale estensione agli ingranaggi. In questo modo per la prima volta è stato possibile calcolare la durata di cuscinetti volventi e ingranaggi esattamente con la stessa metodologia.

Le condizioni tribologiche delle superfici dei fianchi dei denti degli ingranaggi sono simili a quelle delle superfici di contatto dei cuscinetti volventi, ma sono diverse in termini quantitativi. Entrambe le superfici presentano rotolamento/strisciamento (nei cuscinetti lo strisciamento è decisamente ridotto rispetto agli ingranaggi), pressioni elevate (maggiori per i cuscinetti rispetto agli ingranaggi) e rugosità superficiale dello stesso ordine di grandezza dello spessore del film lubrificante. Tutto ciò fa propendere per la possibilità che i metodi di calcolo basati sulla fatica superficiale adottati per le superfici dei cuscinetti volventi possano essere impiegati in modo analogo per le superfici di contatto degli ingranaggi. Un valido esempio in questo senso è il modello dell’affaticamento superficiale di SKF [1], sviluppato in origine per i cuscinetti volventi e poi adottato per gli ingranaggi [2].

Al momento le durate teoriche di ingranaggi e cuscinetti volventi si calcolano in modi diversi. I metodi di scelta e progettazione degli ingranaggi si basano in generale sull’equazione di Lewis [3] per la flessione delle travi. Lo standard AGMA [4] introduce altri fattori di sicurezza nell’equazione di Lewis, che tengono conto della concentrazione delle sollecitazioni alla radice del dente e della distribuzione di carico e sovraccarico sul dente. Oltre alla resistenza alla fatica sulla radice del dente, lo standard AGMA include anche la verifica della condizione di sollecitazione massima sviluppata a livello della superficie di contatto del dente.

Lo standard AGMA introduce un’equazione per la durata superficiale basata su sollecitazioni di contatto “a secco” in modo che, quando la sollecitazione di contatto supera un determinato valore critico, si considera che i denti degli ingranaggi siano soggetti a erosione. Questi metodi sono stati utilizzati con successo negli ultimi decenni per progettare e classificare gli ingranaggi. Tuttavia, con la crescente esigenza del settore industriale di ridurre le dimensioni dei componenti delle macchine e diminuire il consumo energetico e i costi di produzione, gli ingegneri sono costantemente alla ricerca di modi sempre più aggiornati per ottimizzare le dimensioni dei componenti meccanici.

Le più recenti conoscenze tribologiche nell’ambito della lubrificazione automatica, della finitura superficiale avanzata e del controllo della pulizia possono contribuire in modo significativo alla durata degli ingranaggi. Ciò può offrire nuove opportunità per ridurre il sovradimensionamento e aumentare l’efficienza meccanica. Oggi le organizzazioni responsabili degli standard per gli ingranaggi si adoperano con grande impegno per valutare il rischio che si creino erosioni microscopiche (micropitting) sugli ingranaggi [5], a testimonianza dell’importanza di questo argomento nell’ambito della durata degli ingranaggi. Tuttavia, finora gli aspetti tribologici (il cosiddetto rischio di erosioni microscopiche) si possono tenere in considerazione solo indirettamente nel processo di progettazione degli ingranaggi e, contrariamente all’approccio adottato per i cuscinetti volventi, non vi sono linee guida specifiche in merito all’aspettativa della durata dell’ingranaggio.

Per contro, negli anni i cuscinetti volventi hanno tratto vantaggio dalle caratteristiche uniche e specifiche dei modelli per la previsione della durata a fatica del contatto di rotolamento in relazione alle condizioni operative. Le più significative sono:

• l’applicazione della teoria dell’elemento più debole di Weibull della resistenza del materiale [6], che tiene conto del volume della sollecitazione del materiale a rischio;
• l’utilizzo della teoria del coefficiente di carico dinamico di Lundberg-Palmgren [7-8];
• l’approccio statistico nella definizione della durata a fatica, ossia l’affidabilità del 90% per la durata L₁₀;
• l’applicazione del criterio delle sollecitazioni a fatica di Ioannides-Harris [9], che consente l’inclusione dell’effetto della qualità della lubrificazione e della pulizia nella durata a fatica da contatto di rotolamento.

Inoltre, di recente è stato introdotto un nuovo approccio generico per la durata a fatica da contatto di rotolamento: il cosiddetto modello generalizzato di durata dei cuscinetti (GBLM, Generalized Bearing Life Model) [articolo n. 4-2015 SKF Evolution]. In questo nuovo metodo il danneggiamento originato a livello superficiale è formulato in modo esplicito nelle equazioni di base della fatica del contatto di rotolamento e la probabilità di durata della superficie si considera come rischio di cedimento distinto dalle sollecitazioni hertziane della sub-superficie [10-11]. Ciò offre nuove possibilità per l’utilizzo di modelli tribologici specializzati per descrivere cedimenti a livello superficiale del contatto di rotolamento.

Per gli ingranaggi non sono ancora stati utilizzati i concetti di modellazione. Il valore L₁₀ e il coefficiente di carico dinamico non sono mai stati adottati veramente nella progettazione degli ingranaggi, nonostante il notevole impegno profuso negli anni ‘70 grazie al lavoro innovativo di Coy et al. [12-15].

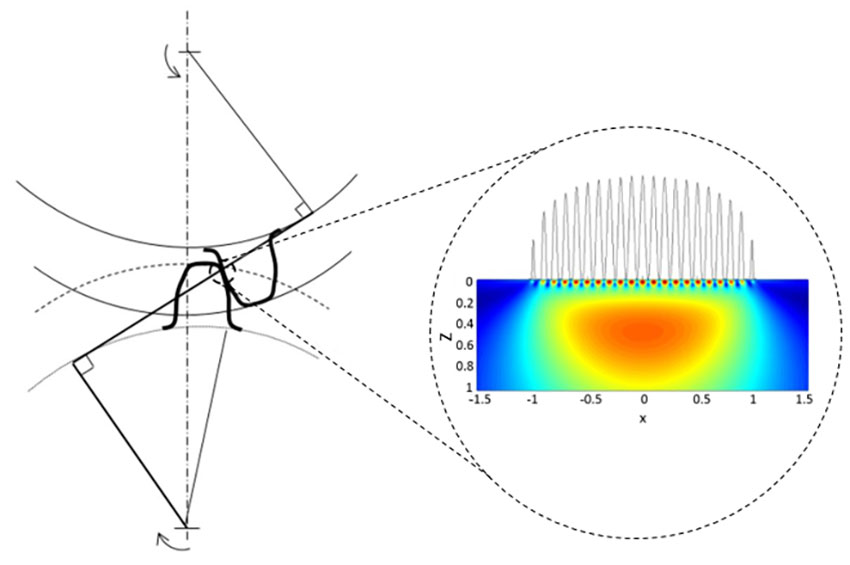
L’obiettivo di questo articolo è analizzare brevemente un adattamento del modello [10] e studiarne la possibile applicazione agli ingranaggi. L’idea principale è descritta in fig. 1. Le aree di sollecitazione della superficie e della sub-superficie del contatto degli ingranaggi sono esaminate separatamente in rapporto al relativo contributo alla durata degli ingranaggi, ma sono entrambe incluse nella stima di L₁₀.

Ciò sarà utile per illustrare i vantaggi del metodo proposto per la valutazione della durata rispetto a quelli attuali e per presentare le possibilità offerte dall’utilizzo di un approccio più integrato per la durata delle superfici di contatto degli ingranaggi.

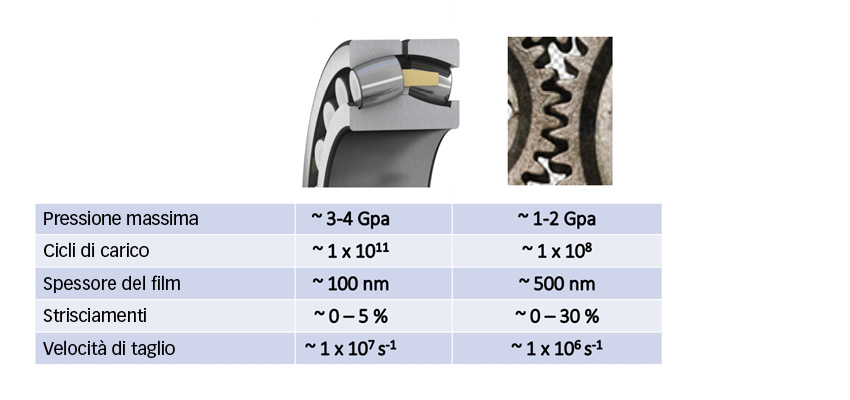
Condizioni tribologiche di cuscinetti volventi e ingranaggi

La fig. 2 mostra un confronto tra ingranaggi e cuscinetti in condizioni tribologiche tipiche. Si può notare che in generale le condizioni nei cuscinetti volventi sembrano più critiche che negli ingranaggi, con pressioni più elevate, durate maggiori e film lubrificanti con spessori inferiori. Tuttavia, gli ingranaggi mostrano maggiore strisciamento e rugosità più elevata, che non favoriscono la durata delle superfici. Oltre a ciò, gli ingranaggi tendono ad avere un orientamento della superficie trasversale rispetto alla direzione di rotolamento/strisciamento, contrariamente a quanto avviene nei cuscinetti volventi, dove in genere la rugosità è orientata nella direzione di rotolamento. Ciò, in condizioni di lubrificazione mista, può essere un vantaggio per i cuscinetti.

La durata di una superficie tribologica in ingranaggi e cuscinetti volventi è determinata principalmente da due importanti fattori: la qualità della lubrificazione e la contaminazione da particelle solide, aspetti presi in considerazione nel calcolo complessivo della durata dei cuscinetti volventi (ISO 281), ma non considerati del tutto nell’attuale calcolo della durata degli ingranaggi. Tuttavia, la recente introduzione della probabilità di sopravvivenza della superficie come rischio di cedimento distinto dalle sollecitazioni hertziane della sub-superficie (il GBLM) potrebbe essere di aiuto per tenere conto degli stessi elementi superficiali sia negli ingranaggi sia nei cuscinetti volventi e per unificare una volta per tutte i metodi di calcolo.

Affaticamento superficiale negli ingranaggi

Se le condizioni di lubrificazione non sono adeguate, gli ingranaggi, come i cuscinetti volventi, potrebbero essere soggetti ad affaticamento superficiale (definito anche erosione microscopica o grey staining, ossia macchiatura grigia). Ciò può avvenire a causa di un olio con viscosità troppo bassa, rugosità troppo elevata negli ingranaggi e velocità bassa. In altre parole, con lubrificante di bassa qualità o rapporto Λ basso.

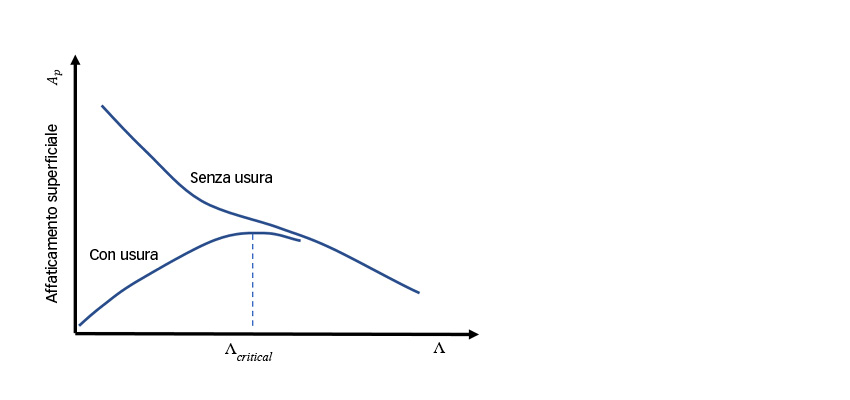
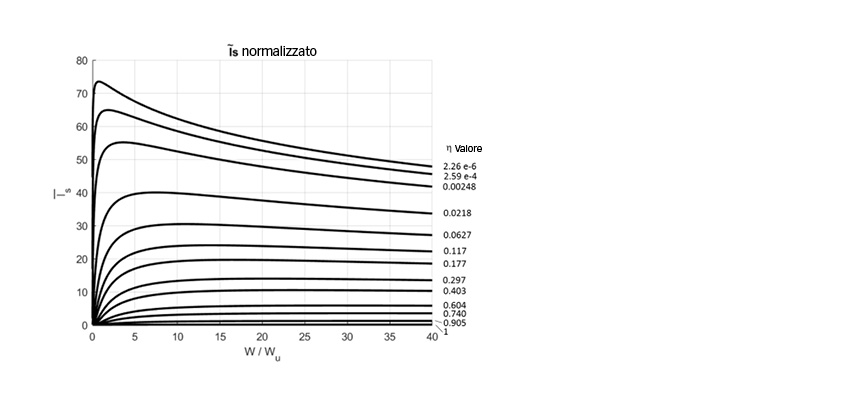
L’affaticamento superficiale si manifesta in corrispondenza delle asperità e può essere contrastato a usura moderata [1–2]. Un’usura moderata potrebbe, infatti, eliminare i picchi delle asperità e ridurre le pressioni locali diminuendo le sollecitazioni superficiali e la fatica e potrebbe inoltre eliminare gli strati di materiale soggetti ad affaticamento. Un’usura moderata troppo bassa potrebbe prolungare la fase di rodaggio delle superfici, causando un danneggiamento maggiore e un affaticamento superficiale più marcato. Per questa condizione valori di Λ inferiori potrebbero comportare un affaticamento superficiale ridotto a causa dell’aumento dell’usura; in caso contrario l’affaticamento superficiale dovrebbe aumentare. Ciò è illustrato in fig. 3.

Un altro aspetto importante dell’affaticamento superficiale negli ingranaggi è la cosiddetta condizione di strisciamento negativo, quando cioè si osserva la superficie più lenta. Spesso si ritiene che la superficie più lenta sia maggiormente soggetta ad affaticamento superficiale rispetto alla superficie più veloce. Questo fenomeno è stato spiegato in [2], dove si dimostra che una superficie più lenta presenta più microcicli di fatica prodotti dalla rugosità della superficie più veloce, oltre ai possibili effetti dovuti all’apertura di cricche superficiali e alla propagazione più rapida.

Durata degli ingranaggi con sopravvivenza di superficie e sub-superficie

Tutti i dettagli del modello proposto sono dati in [16]; tuttavia, in questo articolo è importante indicare l’equazione finale della durata:

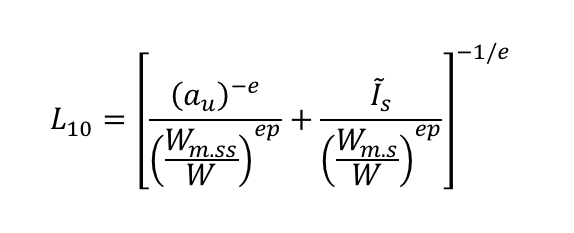
Dove:

Questa equazione della durata (1) ha due termini principali. Il primo (lato sinistro) si riferisce solo alla sub-superficie, dove è possibile applicare le equazioni hertziane classiche. Il secondo termine (lato destro) si riferisce solo alla superficie, dove si utilizzano modelli tribologici più sofisticati [1] per stimare il danneggiamento superficiale. Questa equazione segue gli stessi concetti del GBLM sviluppato per i cuscinetti volventi.

Le equazioni per la capacità di carico dinamico degli ingranaggi (sub-superficie) W_m.ss sono state sviluppate in passato grazie al lavoro di Coy et al. [12-15]. In [16] è stata introdotta un’equazione W_m.s per la capacità di carico dinamico (superficie). Si noti che, a differenza dei cuscinetti, qui è stata introdotta anche una capacità di carico dinamico per la superficie. Nei cuscinetti equivarrebbe a introdurre un valore “C” anche per la superficie.

Fig. 4: Esempio di valore Ĩ_s normalizzato utilizzato negli esempi, con η come fattore ambientale η=η_b η_c (come nei cuscinetti).

Caso di applicazione

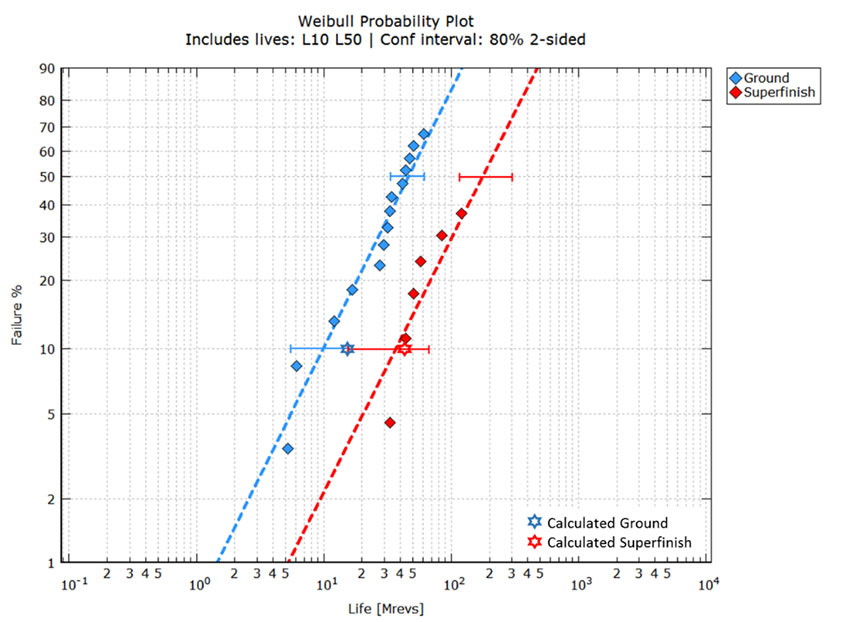
Nel riferimento [17] si confrontano le durate di due gruppi di ingranaggi a denti dritti, uno con superfici molate e l’altro con superfici super-finished. Tutti i dati, i materiali, le geometrie e le condizioni operative degli ingranaggi sono indicati nel riferimento. I due gruppi sono stati testati nelle stesse condizioni operative; tuttavia, il gruppo con superfici molate peggiora con un rapporto Λ inferiore a causa della sua maggiore rugosità (Λ≈1,13), mentre il gruppo con superfici super-finished mostra una qualità della lubrificazione più elevata a causa della sua minore rugosità (Λ≈6,17). I dati dei test rappresentati in [17] per gli ingranaggi con superfici molate e super-finished sono stati digitalizzati e riportati in fig. 5, che mostra una rappresentazione grafica dei dati misurati e calcolati.

In fig. 5 gli intervalli di sicurezza si sovrappongono leggermente e sarebbe necessario un maggior numero di cedimenti (in particolare per la variante con superfici super-finished) per ridurre l’incertezza. Ad ogni modo, grazie a questi dati si può notare che le durate sono chiaramente diverse. La figura mostra anche le durate calcolate utilizzando l’equazione (1) (stelle).

Le durate calcolate sovrastimano leggermente le misurazioni, in particolar modo per la variante con superfici molate rispetto a quella con superfici super-finished. Quando saranno disponibili ulteriori test, sarà possibile calibrare meglio il modello adottando i metodi già utilizzati per i cuscinetti volventi. Tuttavia, in questa fase l’obiettivo principale è fornire una prima valutazione della teoria di base senza l’interferenza dei fattori di calibrazione. In questa prospettiva, come mostrato in fig. 5, il confronto tra i dati dei test e i risultati calcolati utilizzando la metodologia presentata in questo articolo dimostra che esiste un’ottima correlazione.

Conclusioni

Un modello teorico delle durate basate sulla fatica superficiale e sub-superficiale, inizialmente sviluppato per i cuscinetti volventi, è stato ora adattato agli ingranaggi. Come esempio di applicazione si è illustrato l’effetto della qualità della lubrificazione.

Il modello teorico può evolvere in un modello predittivo, una volta calibrato con un maggior numero di risultati sperimentali ottenuti in condizioni di applicazione diverse degli ingranaggi, in particolare tenendo conto dell’effetto del materiale, della lubrificazione, della finitura superficiale e della contaminazione da particelle.

Tuttavia, anche a livello teorico il modello può già fornire valori significativi nei test condotti con ingranaggi a denti dritti, come illustrato nei riferimenti [12-15, 17]. Per la prima volta un modello di durata degli ingranaggi mostra un parametro di coefficiente per la superficie (capacità di carico dinamico superficiale).

Dall’analisi presentata qui, è possibile ricavare le seguenti conclusioni:

1. L’approccio attuale introduce la distinzione tra la sopravvivenza della superficie e della sub-superficie. Pertanto, potrebbero esservi sviluppi significativi aumentando la flessibilità nella modellazione della durata degli ingranaggi, perché si analizzano più aree. Ciò consente agli ingegneri di considerare modalità di cedimento superficiale, oltre alla fatica da contatto hertziano.
2. Poiché gli effetti superficiali sono incorporati direttamente nella formulazione, questo approccio consente di sfruttare le conoscenze acquisite utilizzando modelli tribologici avanzati. In futuro è possibile che vengano introdotti effetti non tribologici, come le sollecitazioni sulla radice del dente.
3. L’introduzione, negli ingranaggi, di una capacità di carico dinamico superficiale in aggiunta alla capacità di carico dinamico sub-superficiale è un’innovazione che offre maggiore flessibilità nella valutazione di ingranaggi con caratteristiche particolari che influiscono chiaramente sulle prestazioni della superficie, come ad esempio i trattamenti, i rivestimenti e le finiture superficiali.
4. In particolare nella progettazione dei rotismi, l’omologazione dei metodi di calcolo della durata tra ingranaggi e cuscinetti volventi sarebbe estremamente utile, per definire non solo le medesime ipotesi per cuscinetti e ingranaggi ma anche per una comune affidabilità.