La fatigue de contact roulant (FCR) est un mode de défaillance typique des roulements et des pièces mécaniques similaires. On doit les principaux travaux relatifs à la FCR à Lundberg et Palmgren [1], [2]. La théorie de Lundberg-Palmgren est principalement axée sur la fatigue de contact roulant en sous-couche et repose entièrement sur des calculs de contraintes hertziennes idéalisées. À l’inverse, la fatigue de contact roulant en surface (FCRS) concerne la zone proche de la surface du contact (profondeur de quelques microns) qui est fortement touchée par les tractions en surface et les contraintes induites par des caractéristiques géométriques de la surface, comme la rugosité, les variations de profil, les empreintes, etc.. L’inter­action entre le film de lubrification élasto-hydrodynamique (EHL) et les caractéristiques réelles qui induisent les concentrations de contraintes à la surface est déterminante dans la compréhension du phénomène de fatigue en surface des roulements (Morales-Espejel et Gabelli [3]). Dans cet article, la progression de la FCRS est étudiée en modélisant le contact et l’inter­action avec les variations de la micro-géométrie de la surface qui génèrent des concentrations de contraintes. La comparaison des simulations numériques avec un ensemble de résultats expérimentaux révèle une bonne corrélation, ce qui permet de formuler une hypothèse concernant les mécanismes sous-jacents de la FCRS, ainsi que son apparition et sa progression dans les roulements. Ces nouvelles connaissances corroborent l’idée élémentaire derrière le SKF Generalized Bearing Life Model (GBLM) ou le Modèle général de la durée du roulement qui distingue les dommages par fatigue en surface de ceux par fatigue en sous-couche [4][5].

Recherches théoriques sur la progression des dommages
Souvent, les dommages par fatigue de contact roulant qui apparaissent autour de caractéristiques microgéométriques de la surface évoluent vers un écaillage. La propagation de l’écaillage, sous sa forme sévère, est fortement influencée par des aspects macrogéométriques : par exemple, l’évolution de la géométrie du contact sur la piste et le champ de contraintes global qui en résulte dans un roulement. Plusieurs chercheurs ont étudié la propagation de l’écaillage dans les roulements en vue de déterminer les aspects mécaniques régissant cette progression.

Des recherches récentes relatives à la propagation de la FCRS dans des roulements pré-indentés, menées par les auteurs du présent article [6] à partir d’un modèle et d’expériences, ont montré que les mécanismes à l’œuvre dans les roulements à billes exigent de prendre en compte les conditions de lubrification et l’interaction entre les contraintes en surface et en sous-couche pour comprendre le développement des fissures typiques en V le long du chemin de roulement, à la différence de la progression des dommages transversaux initiaux observés dans les roulements à rouleaux qui, elle, peut être expliquée de manière satisfaisante à partir d’hypothèses de contacts secs uniquement.

Observations expérimentales de la progression des dommages
Snare [7], dans son analyse statistique de la fiabilité des roulements, a observé la propagation d’un écaillage dans un roulement à rouleaux cylindriques, en montrant la progression nette du dommage en travers de la piste avant que l’écaillage commence à se propager le long de la piste. La Fig. 1 illustre les essais expérimentaux de Snare.

Connaissances actuelles
D’après les recherches théoriques et expérimentales tirées de la littérature, au moins deux phases peuvent être clairement distinguées dans la propagation de l’écaillage à partir de défauts superficiels. La première phase correspond à la propagation de l’écaillage en travers de la piste, à une vitesse plus ou moins lente, et la seconde, à la propagation le long du chemin de roulement à une vitesse plus soutenue. La propagation de l’écaillage en travers de la piste, lors de la phase initiale, est provoquée par des contraintes plus importantes sur les bords diamétraux de l’écaillage, le long d’une direction perpendiculaire à l’axe de roulement, que celles en entrée et en sortie de l’écaillage.

Le comportement relatif à l’initiation et à la propagation de l’écaillage est complètement différent entre les roulements à billes (Fig. 2) et les roulements à rouleaux (Fig. 3). L’écaillage initié en surface dans les roulements à billes se développe dans un premier temps sous la forme caractéristique d’un V au niveau du bord de fuite de l’empreinte, puis se propage rapidement depuis cette zone en V dans le sens de roulement avec un détachement de fragments de matière. La progression de l’écaillage est observée dans le sens de roulement (sens opposé à celui du frottement et du glissement qui s’opèrent à cet endroit (Fig. 2)). L’écaillage initié en surface dans les roulements à rouleaux se propage d’abord des deux côtés du point de départ, puis progresse en travers de la piste avant de s’étendre le long de celle-ci (Fig. 3).

Cet article a pour but d’apporter des éclaircissements sur la progression des dommages par fatigue initiée en surface dans les roulements à rouleaux. Il vise une meilleure compréhension, grâce à la modélisation, des mécanismes sous-jacents à la propagation des dommages observés lors des expériences. Ces recherches s’inscrivent dans le prolongement des travaux évoqués par les auteurs [3] sur la phase initiale des dommages, en se concentrant cette fois-ci sur leur propagation.

Travaux expérimentaux
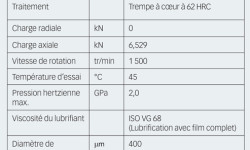
Les expériences ont été réalisées sur des roulements à rouleaux coniques standard (cf. Tableau 1).

Les roulements à rouleaux coniques ont été indentés artificiellement à l’aide d’un pénétrateur à bille en carbure de tungstène de 1 mm de diamètre et en appliquant une charge de 1 250 N. Cette charge a généré des empreintes de 400 μm de diamètre, 30 μm de ­profondeur, avec un rebord de 2 μm. Huit empreintes équidistantes ont ainsi été créées sur la circonférence de la bague intérieure des roulements à rouleaux coniques. Ces empreintes étaient, en outre, décalées tous les 0,5 mm à travers la piste en partant du bord. Dans cet article, nous ne nous intéresserons cependant de manière détaillée qu’à la progression des dommages initiés par les empreintes situées au centre de la piste. Dans les conditions de service indiquées dans le Tableau 1, la charge axiale a donné lieu à un contact hertzien d’environ 142 μm de large dans la direction de roulement, donc nettement moins large que les empreintes. Les expériences ont été réalisées à des moments différents pour observer la progression du dommage par fatigue résultant de la concentration des contraintes et des conditions de lubrification des empreintes.

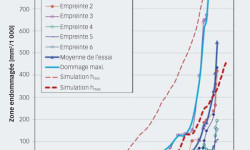
La Fig. 4 illustre certains résultats expérimentaux concernant la propagation de l’écaillage dans le roulement à rouleaux coniques pour un nombre de tours croissant. L’écaillage est apparu d’un côté de l’empreinte, puis a progressé de part et d’autre de cette dernière, en travers de la piste, autrement dit perpendiculairement à la direction de roulement. Sur la Fig. 4(b), une ellipse de contact approximative a été dessinée à des fins de comparaison avec l’écaillage final. Plusieurs bagues intérieures ont fait l’objet d’un suivi : des inspections périodiques de chaque roulement ont été effectuées à l’aide d’un microscope à des intervalles de 5 millions de tours, en vue de détecter les phases d’initiation et de propagation de l’écaillage. Chaque empreinte a été inspectée au microscope et photographiée à différents stades (nombres de tours) au cours de l’essai. Le développement initial et la progression consécutive de la zone écaillée autour de l’empreinte ont été évalués par traitement numérique des microphotographies collectées des différentes empreintes. Cette étude détaillée a permis d’obtenir des informations très précises sur l’apparition et la progression de la zone écaillée selon le nombre de tours. Toutes les données collectées sur les six empreintes ayant causé un écaillage sont présentées sur la Fig. 5.

Une étude plus approfondie des données d’essai moyennes révèle que la progression de la zone écaillée suit un processus en trois étapes :

1. Période d’incubation entre 50 et 60 millions de tours pendant laquelle aucun dommage apparent n’est détecté sur la piste du roulement ; cette période correspond à la durée de vie en fatigue du roulement.
2. La phase de progression initiale des dommages, de 30 à 40 millions de tours, est marquée, comme escompté, par un développement exponentiel de la zone endommagée.
3. Développement accéléré. Au cours de cette phase, d’une durée de 20 à 25 millions de tours, la progression s’accélère (deux fois plus rapidement que la phase précédente).

Modèle de propagation des dommages
Le calcul des dommages au niveau du contact roulant s’effectue, dans un premier temps, par modélisation de l’empreinte initiale sur piste. On recourt, pour ce faire, à une fonction analytique paramétrique qui reproduit la forme de l’empreinte au plus près de la réalité.

La géométrie de l’empreinte est ensuite intégrée à un modèle de contact roulant pour reproduire le cycle de contrainte hertzienne réel sur le roulement utilisé lors de l’essai. Le calcul de la progression des dommages est effectué en appliquant le modèle de base de fatigue en surface et le détachement de matière développé par Morales-Espejel et Brizmer [8] et décrit de manière exhaustive dans ce document. Des modifications et adaptations ont cependant été introduites. Par exemple, la routine pour le calcul de l’usure, décrite dans la référence [8], est laissée de côté pour accélérer les simulations numériques. Le modèle rapide de lubrification est également laissé de côté, et seul le modèle de contact sec est utilisé pour les situations dans lesquelles l’empreinte initiale est plus large que le contact hertzien dans le sens du roulement (comme c’est le cas pour le roulement à rouleaux coniques simulé de la Fig. 4a). Le modèle est ensuite utilisé dans le calcul des pressions et contraintes globales. Cette approximation est valable dans la mesure où, dans le cas qui nous intéresse, le lubrifiant aura tendance à s’échapper de l’empreinte et du contact. Aucune pression hydrodynamique n’étant attendue dans la région du bord de l’empreinte. Les pressions dans cette zone peuvent être modélisées en partant de l’hypothèse d’un contact sec (pour les roulements à billes, sur lesquels la zone de contact hertzien est plus large, le modèle de lubrification ne peut être ignoré).

Une fois les pressions de contact calculées, on obtient l’historique des contraintes pour une série d’étapes visant à simuler le passage de l’empreinte dans le contact roulant (cf. [5]). Ce processus de simulation en plusieurs étapes permet de suivre l’historique des contraintes en fatigue. Cela permettra un traitement supplémentaire selon le critère de fatigue dans le but d’estimer le dommage par fatigue cumulé depuis le début jusqu’au cycle de charge en cours. Cette procédure suit exacte­ment le traitement des données introduit par Morales-Espejel et Brizmer [8]. Le dommage total cumulé jusqu’au cycle de charge en cours est calculé en appliquant la règle de Palmgren-Miner.

Lorsque la valeur critique du dommage en fatigue critique est atteinte, une rupture du matériau peut se produire. La méthode actuelle n’intègre aucun modèle détaillé de propagation des fissures ; la propagation des dommages est simulée par un simple enlèvement de matière. Pour ce faire, un modèle simple d’enlèvement de matière [8] a été développé ; il permet de prendre en compte l’enlèvement de la matière correspondant au dommage critique cumulé et de la matière au-dessus. Ce modèle intègre également un seuil de profondeur (h) par rapport à la surface en dessous duquel la matière présentant un dommage critique ne peut se détacher. Ce seuil de profondeur peut être fixé entre h=0 et h=∞. Si h ≥ 0, un enlèvement de matière sous la surface est possible. Le modèle actuel ne permet pas d’obtenir une indication précise de la progression du dommage si le paramètre h n’est pas connu à l’avance ou si certains résultats expérimentaux ne sont pas disponibles, mais il peut très bien fournir des plages de progression du dommage, comme cela est expliqué ci-dessous. La procédure de calcul est répétée pour un certain nombre de cycles de charge (jusqu’à un maximum généralement supérieur à 10⁹ cycles de charge en roulement), puis l’on obtient l’historique de la progression du dommage.

Résultats fournis par le modèle
Les résultats obtenus lors du test sont indiqués dans le Tableau 1. Dans ce cas précis, les empreintes sont plus larges (diamètre de 400 μm) que le contact hertzien dans la direction du roulement (142 μm) ; par conséquent, la pression EHL requise ne peut être atteinte lors du passage des éléments roulant sur l’empreinte. Il en résulte une détérioration du film d’huile en bordure de la zone indentée. Dans ces conditions, l’effet du film lubrifiant peut être exclu de l’analyse et la progression du dommage peut être simulée en utilisant simplement une approximation de contact sec.

La Fig. 6 illustre l’évolution de l’écaillage depuis l’empreinte initiale en fonction du nombre de tours ; les changements progressifs de la pression hertzienne et des contraintes internes associées sont également représentées. Les résultats des simulations numériques indiquent clairement la direction principale de la progression de la zone écaillée. Le dommage part des bords latéraux de l’empreinte et s’étend dans le sens axial, en travers de la piste, comme cela a été observé lors des expériences (cf. Fig. 4). En calculant la surface endommagée et sa progression dans le temps (nombre de tours), il est possible d’obtenir la courbe de progression de la zone endommagée en fonction du nombre de tours effectué par le roulement. Ce calcul a été réalisé avec deux valeurs de seuil de profondeur, h : une valeur minimum et une valeur maximum pour délimiter la plage des simulations (h_min à proximité immédiate de la zone de contrainte orthogonale maximale autour de l’empreinte et h_max nettement au-delà de cette zone). Les courbes de progression des dommages obtenues apparaissent en pointillés sur la Fig. 5. Les pointillés fins correspondent au résultat obtenu à partir des paramètres les plus conservateurs pour l’estimation du micro-écaillage initié en surface – autrement dit, la valeur minimale du seuil de profondeur. Les résultats des simulations constituent, par conséquent, une délimitation prudente du dommage, définissant les conditions pour la zone de dommage maximale attendue pour tout écaillage initié en surface.

Avec l’intégration d’une valeur de seuil de profondeur maximum, h, l’évolution du dommage représentée sur la Fig. 5 par les pointillés épais présente un rapprochement plus réaliste avec les résultats expérimentaux. La tendance initiale de la zone de dommage calculée apparaît clairement avec une progression qui coïncide avec certaines des mesures expérimentales. Un rythme de progression stable est atteint entre 90 et 120 millions de tours ; cet intervalle est comparable à la phase de progression initiale mesurée concernant l’évolution de la détérioration de l’empreinte que nous avons évoquée dans la section « Travaux expérimentaux ».

Sur la Fig. 7, le rythme de progression de la détérioration mesuré dans les expériences est comparé à celui issu des simulations numériques, qui est de 11,5 millions de tours (134 millions de cycles). Cette excellente corrélation entre la moyenne des résultats expérimentaux et les simulations numériques démontre la capacité du calcul à refléter en partie les principaux effets des mécanismes de fatigue en ­surface et de la progression initiale de l’écaillage. Par ailleurs, les résultats expérimentaux indiquent une accélération de la progression après 100 millions de tours qui semble absente des résultats des simulations numériques. Une explication possible est que la formation d’une zone écaillée se traduit également par des charges supplémentaires dues à la réponse dynamique du roulement à l’écaillage. Pour le moment, ces charges supplémentaires ne sont pas intégrées au modèle ; par conséquent, la comparaison avec les simulations numériques ne peut porter que sur l’écaillage initial.

Dans les résultats des simulations, le mécanisme de progression du dommage est également intéressant. L’empreinte étant légèrement plus large que le contact hertzien dans la direction du roulement, la zone de la piste la plus chargée est la zone latérale de l’empreinte et c’est là, en effet, où le dommage va apparaître et progresser. On retrouve ce même mécanisme de propagation dans la simulation numérique : les pressions de contact et les concentrations de contraintes en sous-couche les plus élevées se situent sur le bord latéral de l’écaillage (Fig. 6). Ce schéma de propagation de l’écaillage semble caractéristique des roulements à rouleaux.

Discussion et conclusions
Les expériences ont été réalisées sur des roulements à rouleaux coniques. Les pistes de ces roulements ont été indentées avec un pénétrateur de dureté définie. Cette opération a ainsi produit une série de contraintes en surface qui ont conduit à l’apparition et la propagation d’un écaillage en surface. Un modèle existant pour la fatigue de la microgéométrie en surface (Morales-Espejel et Brizmer [8] ; fatigue de surface) a été adapté pour l’étude du processus de macro-écaillage initié en surface.

Le modèle a été appliqué afin de mieux comprendre les phases d’apparition et de propagation initiale de l’écaillage. D’après les résultats du calcul, le modèle numérique est parfaitement adapté pour simuler et expliquer de nombreuses observations expérimentales. Il a été montré notamment que dans le cas d’un roulement à rouleaux coniques, l’écaillage se propage dans un premier temps en travers de la piste, c’est à dire perpendiculairement à la direction de roulement. En général, dans les roulements à contact linéaire, les contraintes sont plus élevées sur les bords latéraux de l’empreinte. Ces contraintes plus élevées induisent le développement de l’écaillage en travers de la piste lors de la phase initiale de propagation.

D’après les résultats des travaux actuels, il est possible de tirer les conclusions suivantes :

1. Sur des roulements à rouleaux pré-indentés, l’écaillage se propage dans un premier temps en travers de la piste sous l’effet des contraintes supérieures sur les bords de l’écaillage perpendiculairement à la direction du roulement, comme cela était déjà décrit dans la littérature.

2. Le modèle présenté décrit parfaitement les deux mécanismes de propagation de l’écaillage. En ce qui concerne l’écaillage des roulements à rouleaux en particulier, une bonne corrélation entre la prédiction du modèle et les mesures expérimentales pour la rapidité de progression initial de l’écaillage a été mise en évidence.

Remerciements
Le projet a été financé en partie par une bourse Marie Curie Industry-Academia Partnerships and Pathways (IAPP) de la Commission européenne dans le cadre du projet iBETTER.

http://cordis.europa.eu/project/rcn/109976_en.html

Références
[1] G. Lundberg et A. Palmgren (1947) : « Dynamic Capacity of Rolling Bearings », Acta Polytechnica 1(3), pp 1–52
[2] G. Lundberg et A. Palmgren (1952) : « Dynamic Capacity of Roller Bearings », Acta Polytechnica 2(4), pp 96–127
[3] G.E. Morales-Espejel et A. Gabelli (2011) : « The Behavior of Indentation Marks in Rolling Sliding Elastohydrodynamically Lubricated Contacts », Tribology Transactions 54, pp 589–606
[4] G.E. Morales-Espejel, A. Gabelli, A. de Vries (2015) : « A Model for Rolling Bearing Life with Surface and Subsurface Survival – Tribological Effects » à paraître dans Tribology Transactions
[5] G.E. Morales-Espejel et A. Gabelli (2015) : « Modèle généralisé de durée de vie des roulements SKF ou la puissance de la tribologie », Evolution n° 4-2015, pp 22-28
[6] G.E. Morales-Espejel et A. Gabelli (2015) « The Progression of Surface Rolling Contact Fatigue Damage of Rolling Bearings with Artificial Dents », Tribology Transactions 58, pp 418-431
[7] B. Snare (1970) : « How Reliable Are Bearings? », Ball Bearing Journal 162, pp 3–7
[8] G.E. Morales-Espejel et V. Brizmer (2011) : « Micropitting Modelling in Rolling–Sliding Contacts: Application to Rolling Bearings », Tribology Transactions 54, pp 625–643