Usure et fatigue de surface dans les roulements
L’usure dans les roulements est difficile à prédire, y compris avec des observations, des mesures et une surveillance attentive. SKF a consacré de nombreuses recherches et analyses à l’étude du glissement, de l’usure et de leur impact sur la durée de vie des roulements.
Dans certaines applications, les roulements peuvent subir une perte de matériau (usure) significative résultant d’une lubrification insuffisante, de particules abrasives, de la corrosion ou d’un fonctionnement avec oscillations, entre autres causes. Cette usure peut, à son tour, avoir un effet néfaste sur le fonctionnement des roulements, qui peut aller de la réduction de la précharge jusqu’à des conséquences potentiellement catastrophiques. Une conséquence commune et probablement inattendue d’une usure irrégulière des pistes de roulements est un risque accru de fatigue de surface. Dans certaines applications, il n’est pas rare d’observer des bandes de fatigue ou écaillage de surface le long des pistes. Ce phénomène est lié à la modification du profil des pistes qui peut s’opérer sous l’effet d’une usure irrégulière et se traduire par une concentration des contraintes au niveau des lignes de pression élevée et une diminution de l’épaisseur du film lubrifiant.
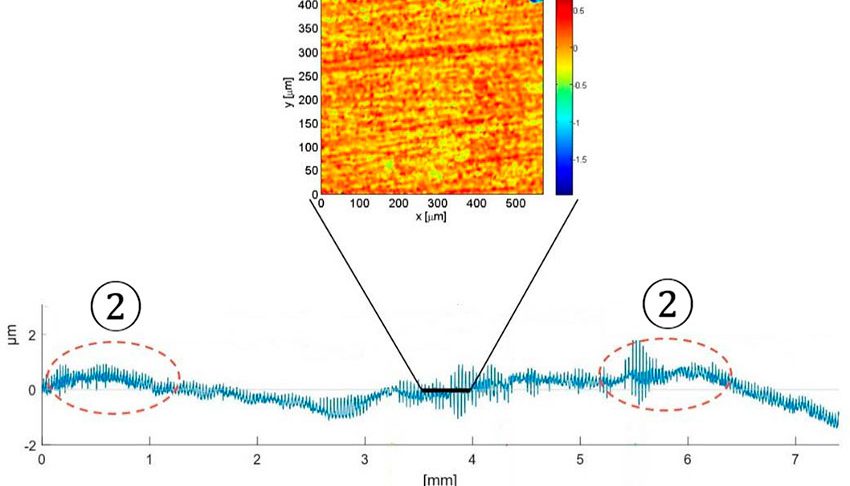
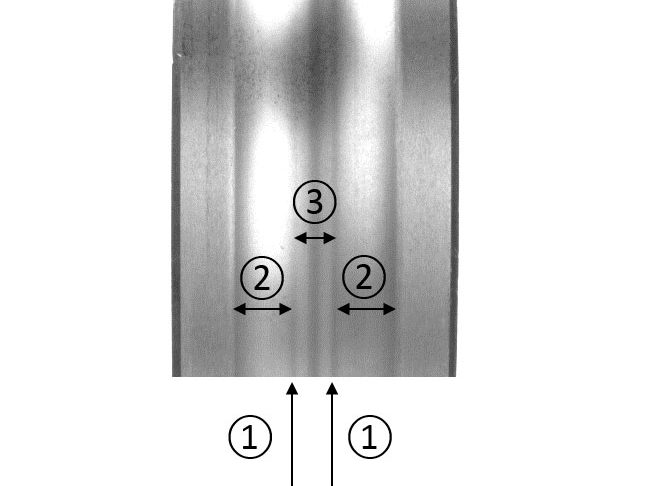
Cette modification des profils des pistes peut être particulièrement marquée dans les roulements utilisés dans des conditions de lubrification médiocre, avec un glissement irrégulier ou en présence de particules abrasives ou de contamination par des liquides (Fig. 1). Sur la durée, de telles modifications induisent des concentrations de contraintes dans les zones les plus fortement chargées (Fig. 2) avec, pour conséquence, une augmentation de la fatigue de surface et l’apparition de bandes de (micro)-écaillage le long des pistes dans ces zones (Fig. 3). N’importe quel roulement peut être sujet à ce mode d’endommagement, mais les applications caractérisées par une forte contamination, une corrosion, une lubrification médiocre, un glissement irrégulier ou une charge variable sont les plus propices à ce phénomène. Les exemples sont nombreux au sein de l’exploitation minière, de l’industrie papetière, de l’éolien et d’autres domaines encore.
L’usure dans les roulements est un phénomène non-linéaire, et des observations et mesures de l’usure à intervalles réguliers montrent que l’intuition ne suffit pas pour prédire son évolution dans le temps. Les raisons en sont multiples : l’usure dépend principalement du glissement local et de la charge locale et, en même temps, influe elle-même sur ces deux facteurs. Par conséquent, une simple interpolation n’est pas envisageable et une analyse plus rigoureuse s’impose ; c’est pourquoi SKF consacre des efforts à la recherche sur le glissement et l’usure dans les roulements et sur leurs effets relatifs à la durée de service de ceux-ci [1].
Dans tout roulement s’opère un glissement plus ou moins important. Il s’agit là d’un phénomène normal qui est dû à la géométrie interne du roulement et/ou aux conditions de charge. Par exemple, un roulement radial à billes ou rouleaux, soumis à une charge purement radiale, présentera également un glissement (microglissement Heathcote) dû à la géométrie du contact entre la bague et l’élément roulant ainsi qu’à la déformation élastique induite par la charge (Fig. 4a et 4b). Étant donné que l’usure dépend du glissement, on pourrait penser qu’à terme (si les conditions indiquées sont exactes), les bandes de roulement pur (A et A1) soient les seules zones épargnées par l’usure et, par conséquent, les seules zones à supporter toute la charge dans le contact.
Heureusement, cela n’est susceptible de se produire que dans des situations d’usure sévère, par exemple en présence de particules abrasives, de corrosion importante ou de glissement anormal dû à une charge inappropriée ou à un montage incorrect du roulement. Dans la plupart des cas, les roulements fonctionnent correctement et ce glissement fait partie des conditions de service normales.
Cet article analyse de manière un peu plus approfondie les principaux mécanismes du mode de dommage potentiel basé sur la combinaison fatigue-usure. La modélisation et les expériences réalisées ont pour but d’améliorer la compréhension de ce phénomène et d’apporter certains éclairages à visée préventive.
Modélisation
Modélisation de l’usure
Le document de référence [2] traite de différents modèles d’usure dans différentes conditions de lubrification et conclut que le modèle d’Archard [3] est adapté dans tous les cas, même si un modèle de coefficient d’usure plus élaboré peut parfois être nécessaire. Dans la plupart des cas, le coefficient d’usure est un facteur empirique basé sur l’expérience. L’équation d’usure est, par conséquent, généralement la suivante :
où :
V = volume d’usure [m3] à un moment donné,
![]() = coefficient d’usure sans dimension d’Archard [-],
= coefficient d’usure sans dimension d’Archard [-],
F = force de contact [N],
H = dureté du matériau de surface [Pa],
s = distance de glissement [m] à un moment donné.
Le volume d’usure peut être exprimé comme suit :
où :
h = épaisseur de la couche superficielle enlevée [m] à un moment donné,
As = surface de glissement [m2] à un moment donné.
Ainsi, en appliquant l’équation (2) à l’équation (1) et en considérant la pression moyenne de contact ![]() :
:
Si l’on considère ensuite le temps total de contact ![]() par cycle de charge, qui correspond à la durée du passage des deux surfaces de glissement à travers la zone de contact à la vitesse de glissement, la zone de glissement correspond alors simplement à la zone de contact, par conséquent As = A. L’épaisseur de la couche enlevée pour un nombre de tours (N) donné peut être calculée d’après le document [2] comme suit :
par cycle de charge, qui correspond à la durée du passage des deux surfaces de glissement à travers la zone de contact à la vitesse de glissement, la zone de glissement correspond alors simplement à la zone de contact, par conséquent As = A. L’épaisseur de la couche enlevée pour un nombre de tours (N) donné peut être calculée d’après le document [2] comme suit :
où :
us = vitesse de glissement locale [m/s],
u1 = vitesse moyenne de la surface analysée [m/s],
l = longueur de contact dans le sens du glissement [m].
Il convient de noter que pratiquement toutes les valeurs sont locales (x,y.) Par ailleurs, la dureté de l’acier dans les pistes et les éléments roulants est considérée ici comme constante. L’équation (4) permet d’obtenir l’épaisseur locale de la couche usée enlevée à chaque passage dans un contact de roulement.
Modélisation de l’interaction usure-fatigue
Pour modéliser l’interaction usure/fatigue dans les roulements, il convient d’appliquer un modèle de fatigue de contact de roulement (FCR) à chaque passage des éléments roulants sur la piste avec un profil préalablement modifié (sur les deux surfaces) par l’usure ; les deux phénomènes (usure et fatigue) sont ainsi en interaction. Chaque fois que l’usure modifie le profil, une nouvelle répartition de la pression dans le contact doit être calculée pour le modèle de fatigue. Ce processus reflète ce qui se produit en situation réelle. Il s’avère toutefois très gourmand en calculs puisqu’on considère généralement des durées en FCR de l’ordre de plusieurs millions de passages. Certaines simplifications peuvent cependant permettre de réduire nettement les coûts de calcul :
- le calcul porte sur un contact sec au lieu d’un mécanisme de lubrification élasto-hydrodynamique (EHL) avec film complet, omettant ainsi la solution au problème de lubrification en considérant simplement un coefficient de frottement fixe (mesuré) ;
- actualisation du profil modifié par l’usure tous les n passages des éléments roulants, et non à chaque passage ;
- il découle, en outre, du point (2) que l’actualisation du calcul du contact et du calcul du dommage (fatigue) peut être réalisée simultanément à l’actualisation du profil modifié par l’usure et non pas à chaque passage des éléments roulants.
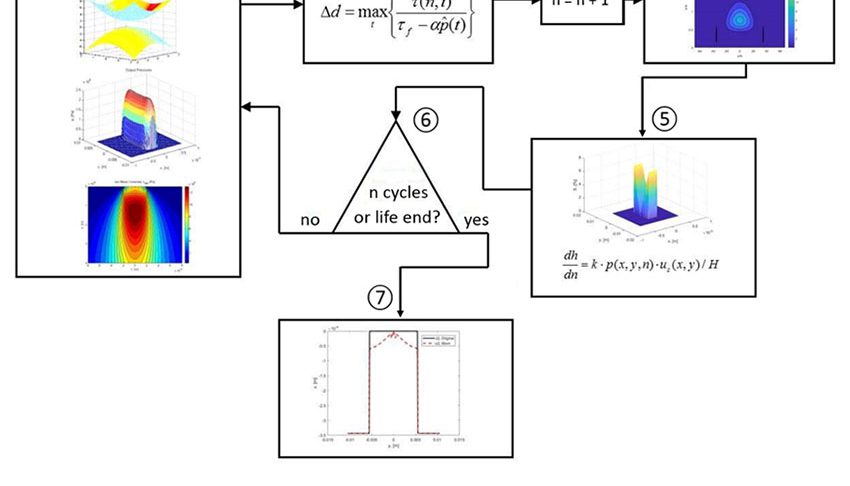
Le schéma de la Fig. 5 résume le déroulement du calcul. Notez qu’on utilise dans ce cas le critère de fatigue de Dang Van [4], ainsi que la règle du cumul linéaire des dommages de Palmgren-Miner [5, 6]. Tout autre critère de fatigue ou charge de cumul des dommages aurait pu être utilisé si les expériences en avaient souligné la pertinence.
Expériences
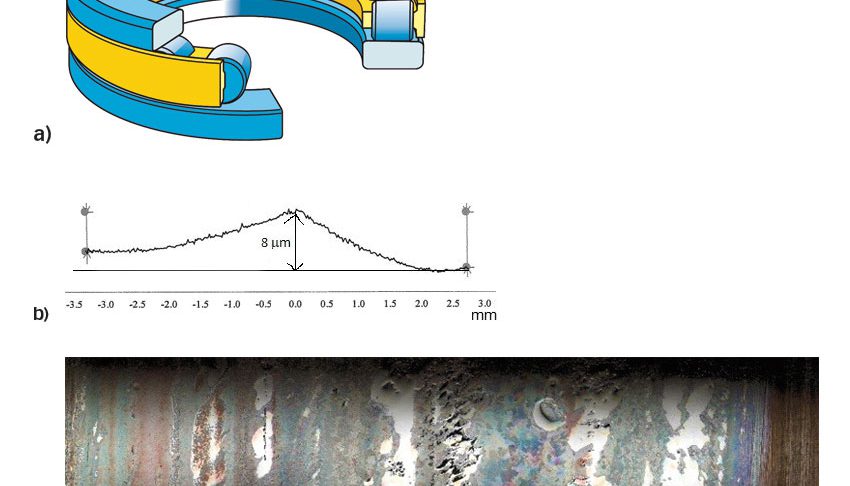
Pour confirmer le modèle de fatigue, un essai d’endurance a été réalisé avec une butée à rouleaux cylindriques 81107 TN (Fig 6a), chargée axialement avec C/P = 6,5, et des conditions de lubrification caractérisées par ![]() ≈ 0.5.
≈ 0.5.
Préalablement à l’essai, le profil des roulements neufs a été modifié artificiellement (Fig. 6b) comme s’ils avaient fonctionné dans des conditions d’usure sévère. Pendant l’essai, certains roulements ont présenté des avaries liées principalement à des dommages des rouleaux (Fig. 6c) et le modèle de durée a ainsi pu être comparé aux résultats du court essai. Les mêmes rouleaux usés et des rondelles neuves ont été pris en compte dans le modèle de la Fig. 5 ; les résultats ont montré une excellente concordance avec la limite inférieure de la durée de vie L10 mesurée en appliquant les statistiques de Weibull.
En parallèle, des essais d’usure et des mesures sur des roulements complets ont également été réalisés afin de calculer le coefficient d’usure, puis de valider le modèle. La concordance entre le modèle et les expériences était une fois encore satisfaisante.
Résultats
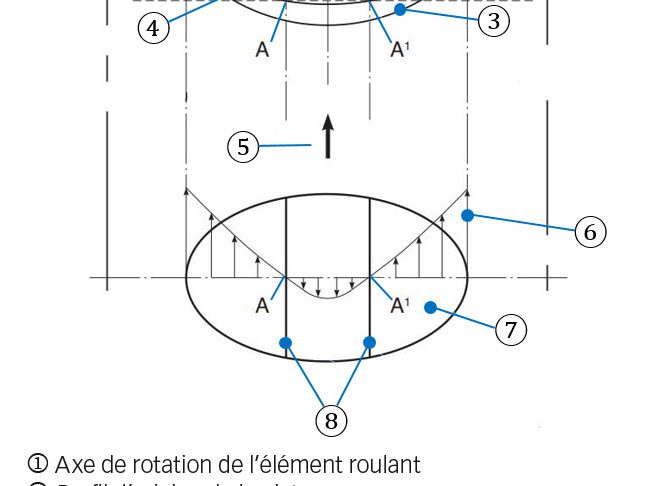
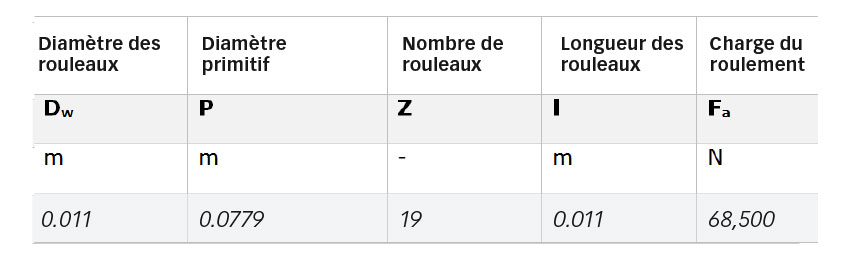
Dans les butées à rouleaux cylindriques, le glissement varie (diminue) de façon linéaire depuis les deux extrémités du rouleau vers la ligne primitive où il tombe à zéro (Fig. 7). En progressant vers le diamètre extérieur du roulement, la vitesse à la surface des rouleaux augmente et, à l’inverse, elle diminue vers le diamètre intérieur. Pour illustrer les effets concomitants de l’usure et de la fatigue dans un roulement avec un glissement qui varie dans la largeur de piste, un autre cas a été étudié avec un roulement plus large (81212 TN), conformément aux informations du Tableau 1.
Une simulation a été lancée, dans laquelle le modèle peut modifier le profil soumis à l’usure par le biais d’un coefficient d’usure dimensionnel (selon la formule ![]() ), dans les conditions de charge indiquées dans le Tableau 1, avec le projet d’atteindre une durée nominale de 300 millions de passages des éléments roulants.
), dans les conditions de charge indiquées dans le Tableau 1, avec le projet d’atteindre une durée nominale de 300 millions de passages des éléments roulants.
Au lieu d’actualiser le profil modifié par l’usure à chaque passage des éléments roulants, il a été déterminé que les actualisations pouvaient s’effectuer tous les 15,5 millions de tours. Pour la simulation, le modèle appliqué est le même que sur la Fig. 5, en incluant le modèle d’usure d’Archard de l’équation (4).
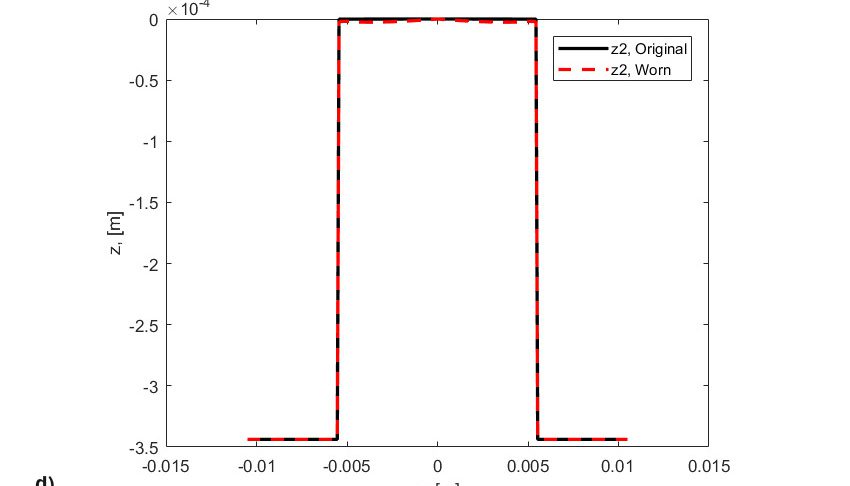
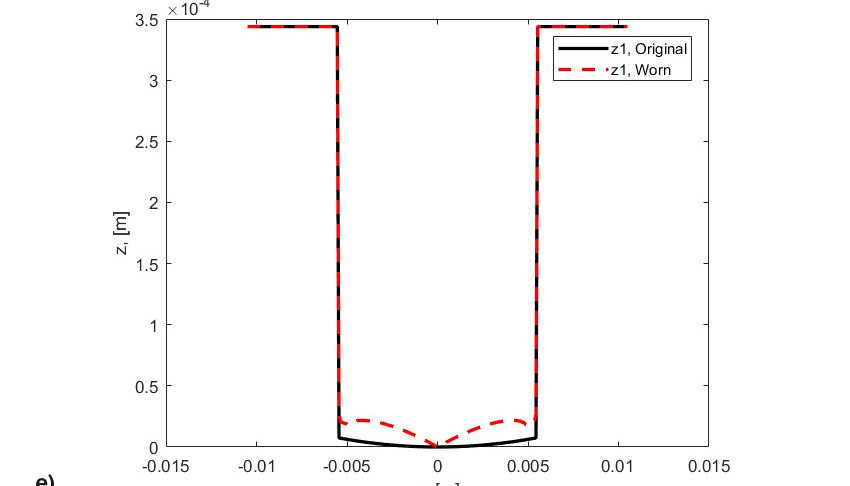
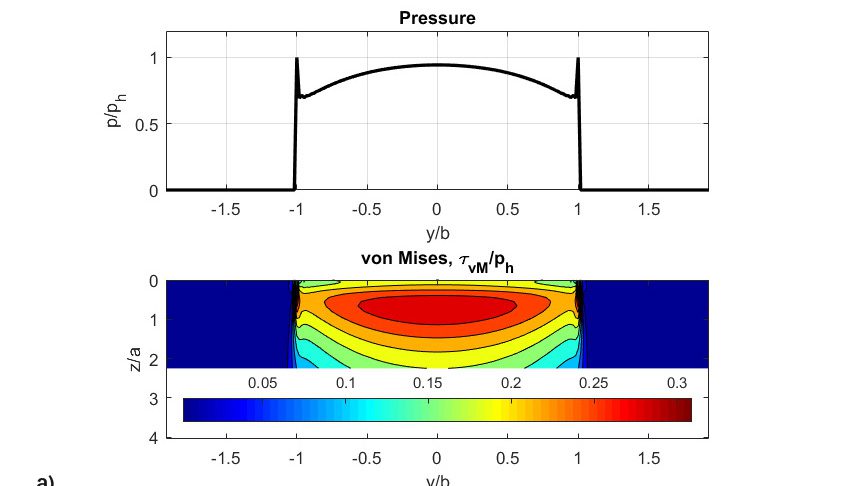
Les résultats de la simulation sont présentés sur la Fig. 8. Cette figure indique :
- les pressions sans dimension,
- les contraintes de cisaillement von Mises,
- la carte des dommages,
- les profils d’origine du rouleau et de la rondelle,
- les profils usés du rouleau et de la rondelle, correspondant au stade final des simulations.
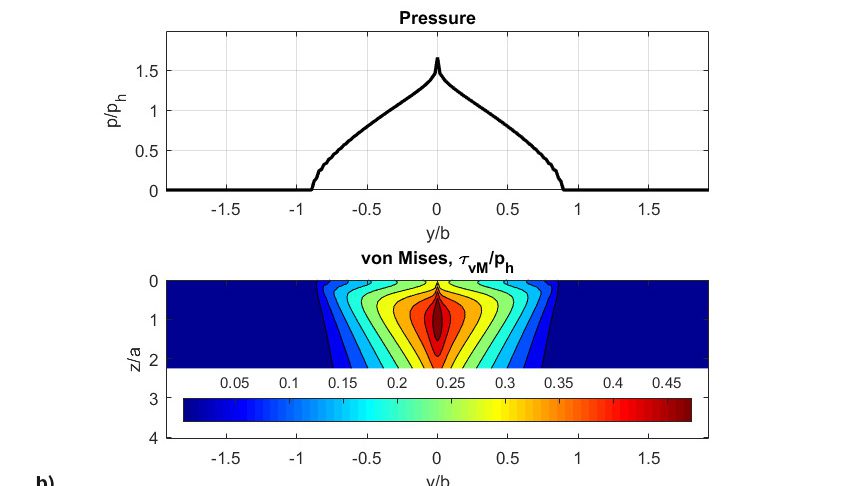
Il est important de souligner que la carte des dommages a dépassé la valeur totale de dommages de 1 (seuil de déclenchement de la fissuration) au bout de seulement 31 millions de tours. Les résultats représentés sur la Fig. 8 se rapportent aux stades initial et final de la simulation. La pression initiale (Fig. 8a) au premier passage des éléments roulants ressemble plus ou moins à une pression hertzienne, mais on observe un certain effet de contrainte de bord car le profil utilisé est un profil simple de rouleau droit, tandis qu’un rouleau au profil adéquat permettrait d’éviter ce type de contraintes de bord. Les résultats montrent clairement un glissement nul sur la ligne primitive. La partie de la simulation ayant trait au modèle d’usure d’Archard indique une usure également nulle à cet endroit.
L’usure est en effet liée à la distribution du glissement à travers la piste. Ainsi, plus on s’éloigne de la ligne primitive de la piste, plus le développement de l’usure est rapide. Il convient de noter que la pression de contact était à l’origine pratiquement rectangulaire (Fig. 8a), mais du fait de l’enlèvement de matière des deux côtés du contact roulant, la pression est réduite dans les zones de glissement important et nettement accrue et concentrée dans la zone de glissement nul (ligne primitive), (Fig. 8b). Cette pression accrue génère des contraintes élevées et une fatigue importante dues à une vitesse supérieure, jusqu’à la survenue d’une avarie au milieu du rouleau (Fig. 8c). L’effet simultané et concomitant de l’usure et de la fatigue peut en effet accélérer l’écaillage par FCR du contact. Cet écaillage de fatigue accéléré n’est pas lié à la contrainte de frottement induite par le glissement, mais résulte d’une modification du profil original des éléments roulants (Fig. 8d et 8e) qui se traduit par une brusque concentration de contraintes de contact et une plus faible épaisseur de film localement.
Résumé
La modélisation des effets concomitants de l’usure abrasive et de la FCR révèle le rôle potentiellement important du glissement dans l’augmentation de l’endommagement de fatigue d’un roulement. Cela exige la présence de particules abrasives et/ou de conditions de lubrification très médiocre dans le roulement. Une distribution du glissement non uniforme dans le contact hertzien contribue également à générer des concentrateurs de contraintes qui raccourcissent rapidement la durée de service du roulement. Il semble en effet qu’il s’agisse du mécanisme le plus significatif à travers lequel le glissement hertzien puisse réduire la durée en FCR du roulement.
Les recommandations pour réduire ce risque sont les suivantes :
- veillez à ce que le roulement soit toujours correctement lubrifié, notamment pour les roulements de grandes dimensions caractérisés par de faibles vitesses de rotation ou d’oscillation et les roulements exposés à la présence de particules abrasives en grande quantité ou à la corrosion ;
- optimisez les solutions d’étanchéité, utilisez des roulements avec flasques/avec joints ;
- limitez autant que possible la contamination solide et liquide ;
- évitez les charges avec chocs et les vibrations susceptibles d’augmenter nettement le glissement nominal dans le roulement ;
- dans le cas de roulements de grandes dimensions, si une usure irrégulière est détectée à temps, une réparation peut être une solution envisageable pour réduire les coûts.
Auteur :
Guillermo E Morales-Espejel,
scientifique en chef, SKF Research & Technology Development, Nieuwegein (Pays-Bas)
L’auteur tient à remercier Ralph Meeuwenoord pour son précieux soutien lors de la phase expérimentale de ce projet.
References
[1] Morales-Espejel, G.E., Gabelli, A., Rolling Bearing Seizure and Sliding Effects on Fatigue Life, Proc. IMechE, part J, Journal of Eng. Tribology, DOI: 10.1177/1350650118779174, 2018.
[2] Morales-Espejel, G.E., Brizmer, V., Piras, E., Roughness Evolution in Mixed Lubrication Condition due to Mild Wear, Proc. IMechE, part J, Journal of Eng. Tribology, 229(11), pp. 1330-1346, 2015.
[3] Archard, J.F., Contact and Rubbing of Flat Surface, Journal of Applied Physics; 24(8): 981–988, 1953.
[4] Dang Van, K., Griveau, B., and Message, O., On a New Multiaxial Fatigue Limit Criterion: Theory and Application, Biaxial and Multiaxial Fatigue, Brown, M. and Miller, K. (Eds.), Mechanical Engineering Publications: London, pp. 479-498, 1989.
[5] Palmgren, A., Die Lebensdauer von Kugellagern [Life Length of Roller Bearings], Zeitschrift des Vereines Deutscher Ingenieure (VDI Zeitschrift), 68(14), 1924,
pp 339-341. (In German)
[6] Miner, M.A., Cumulative Damage in Fatigue, Journal of Applied Mechanics, 67 A157, 1945.








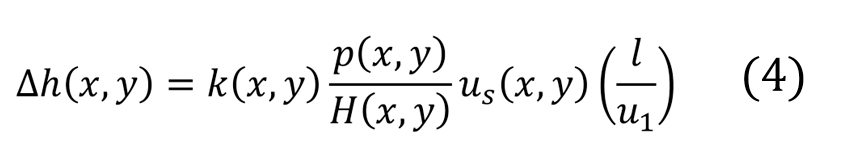

![c) Carte de dommages Palmgren-Miner à l’issue d’une simulation, conformément aux données du Tableau 1, avec un coefficient d’usure de k =0,5x10-11 [s]. c) Carte de dommages Palmgren-Miner à l’issue d’une simulation, conformément aux données du Tableau 1, avec un coefficient d’usure de k =0,5x10-11 [s].](https://evolution.skf.com/wp-content/uploads/sites/5/2019/06/wear-and-surface-fatigue-in-rolling-bearings-fig8c-1-850x486.jpg)