Profondità ottimale dello strato cementato per le prestazioni dei cuscinetti

Per migliorare la resistenza all’usura e la capacità di carico, le superfici di contatto dei cuscinetti sono sottoposte a trattamenti termici specifici. A seconda di fattori quali le dimensioni del cuscinetto e le tipologie di acciaio utilizzate, i componenti possono essere sottoposti a tempra a cuore o superficiale. La tempra a cuore è adatta per gli acciai ad alto tenore di carbonio, mentre per gli acciai a basso tenore di carbonio (< 0,25% di carbonio) è necessaria la tempra superficiale, ottenuta mediante processi come la cementazione. La tempra superficiale per induzione è un altro metodo ampiamente utilizzato per gli acciai a medio tenore di carbonio.

La cementazione prevede la diffusione di una fonte di carbonio a temperature elevate nell’acciaio a basso tenore di carbonio, che forma uno strato cementato dopo il raffreddamento per tempra. La capacità di carico dei cuscinetti sottoposti a tempra superficiale dipende da fattori quali la profondità dello strato cementato e la resistenza del cuore. I produttori di cuscinetti devono scegliere con cura le tipologie di acciaio e garantire una profondità dello strato cementato adeguata a specifiche applicazioni. Tuttavia, una profondità eccessiva dello strato cementato non solo aumenta i costi di produzione non necessari, ma può anche portare alla formazione di cricche durante la tempra e a effetti indesiderati come l’ossidazione intergranulare e l’ingrossamento dei grani [1].

Lo schiacciamento del cuore [2, 3], una modalità di cedimento nei cuscinetti sottoposti a tempra superficiale, deriva da una profondità dello strato cementato insufficiente o da carichi di contatto eccessivi, oppure da una combinazione di entrambi i fattori. Questo cedimento comporta l’innesco e la propagazione delle cricche nel cuore del materiale sotto lo strato temprato. La differenza di durezza tra lo strato superficiale e il cuore contribuisce in modo significativo allo schiacciamento del cuore, perché le sollecitazioni derivanti dal contatto di rotolamento possono superarne la resistenza statica o a fatica. Negli studi di Alfredsson e Olsson [4] e di Lai et al. [5] si è osservato lo schiacciamento del cuore in campioni sottoposti a tempra superficiale e a carico di fatica da contatto statico; quest’ultima è una prova che prevede l’improntatura ciclica della superficie del campione con una sfera o un rullo. Le simulazioni numeriche [5] hanno rivelato che profondità ridotte dello strato cementato o carichi di contatto eccessivi inducono sollecitazioni di trazione residue significative nell’area di transizione tra strato cementato e cuore, portando alla formazione di cricche laterali in condizioni di carico di fatica da contatto statico. La forte plasticità del cuore indebolisce il suo supporto allo strato cementato, con la conseguente flessione dello strato cementato e la possibile formazione di cricche se si superano i limiti di sollecitazione. Oltre allo schiacciamento del cuore, la capacità di carico statico dei cuscinetti sottoposti a tempra superficiale è indicata dalla deformazione plastica in condizioni di carico di contatto statico. Tuttavia, il coefficiente di carico statico definito nella norma ISO 76 [6] non prende in considerazione i cuscinetti sottoposti a tempra superficiale. Sono stati proposti metodi di calcolo [5] per valutare l’improntatura plastica delle piste nelle ralle di orientamento sottoposte a tempra superficiale per induzione.

Questo articolo si basa su uno studio che abbiamo pubblicato di recente [7] con l’obiettivo di caratterizzare e modellare il comportamento dei materiali dei cuscinetti cementati in condizioni di fatica da contatto statico. Mediante la valutazione dell’improntatura plastica superficiale e del rischio di schiacciamento del cuore, la ricerca offre spunti per gli ingegneri e i produttori, in particolare nell’ottimizzazione delle prestazioni dei cuscinetti cementati.

Modellazione e simulazione numeriche

L’interazione tra un corpo volvente e la superficie della pista nell’anello di un cuscinetto cementato viene simulata utilizzando l’analisi a elementi finiti con il codice commerciale ABAQUS. La simulazione comprende tre tipi di contatto: contatto puntiforme, contatto lineare e contatto ellittico.

Dato che ci concentriamo sulla comprensione della risposta dei materiali ai carichi di contatto statico, il comportamento elastoplastico dei materiali è fondamentale nel modello a elementi finiti. Per descrivere la deformazione elastoplastica si utilizza la relazione sollecitazione/deformazione, tipicamente derivata da prove di trazione o compressione. Poiché la resistenza del materiale è strettamente legata alla durezza, correliamo il gradiente di resistenza nel componente cementato al profilo di durezza. Una volta definite le curve di sollecitazione/deformazione per la struttura del cuore e per quella dello strato cementato attraverso prove di compressione, utilizziamo l’interpolazione lineare per approssimare la relazione sollecitazione/deformazione per i materiali con qualsiasi altra durezza.

Il modello a elementi finiti favorisce la valutazione dell’improntatura plastica superficiale e dei danneggiamenti sotto la superficie risultanti da carichi di contatto statici. Attraverso uno studio parametrico che comprende condizioni di carico e profili di durezza diversi, si ricavano equazioni empiriche che esprimono la deformazione plastica della pista in funzione della profondità dello strato cementato, della durezza dello strato cementato e del cuore, del diametro del corpo volvente e della pressione di contatto. Inoltre, lo studio consente di stabilire i limiti di tolleranza per i danneggiamenti sotto la superficie negli anelli di cuscinetti cementati sottoposti a condizioni di carico di contatto statico.

Si consideri un componente con durezza uniforme, analoga alla tempra passante o alla struttura del cuore prima della cementazione. L’improntatura plastica superficiale (δ) è correlata alla pressione di contatto massima (p₀) e alla resistenza allo snervamento del materiale (σ_y) come:

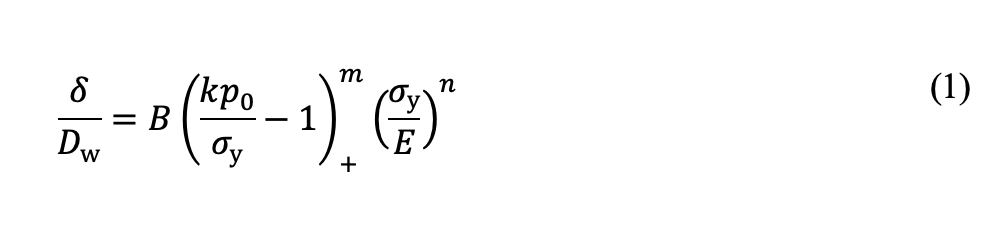
Qui, D_w è il diametro dell’elemento di rotolamento e (…)₊ rappresenta la parentesi di McCauley, che imposta il termine a zero se la quantità tra parentesi è negativa. La costante k, indipendente dai materiali, collega la pressione di contatto p₀ e le sollecitazioni massime di von Mises σ_vM (σ_vM = kp₀). Per il contatto puntiforme k = 0,62, mentre per il contatto lineare k = 0,56. Le costanti B, n e m sono specifiche del materiale.

Se il componente viene sottoposto a cementazione e tempra, l’improntatura plastica deriva dalla deformazione dello strato cementato e del cuore. La loro suddivisione dipende dalla profondità relativa dello strato cementato (h_c /D_w). In questo caso, la profondità dello strato cementato h_c è definita come la profondità alla quale la durezza è uguale a HV550. Secondo lo studio di Lai et al. [5]:

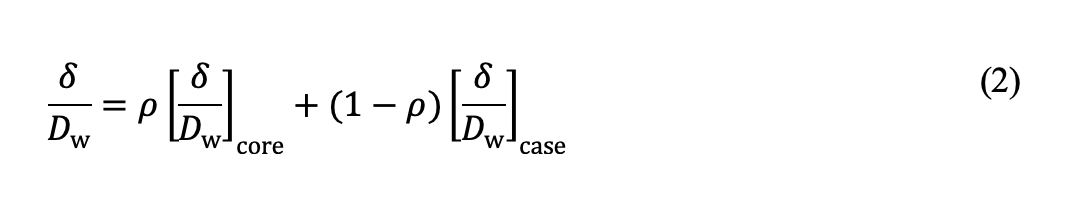
dove [δ /D_w]_core e[δ /D_w]_casee sono, rispettivamente, le improntature plastiche dei materiali del cuore e dello strato cementato date dall’equazione (1), il parametro di suddivisione ρ nell’equazione di cui sopra è una funzione della profondità relativa dello strato cementato h_c /D_w e della pressione di contatto:

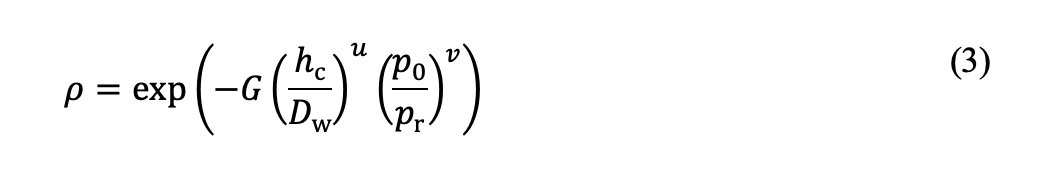
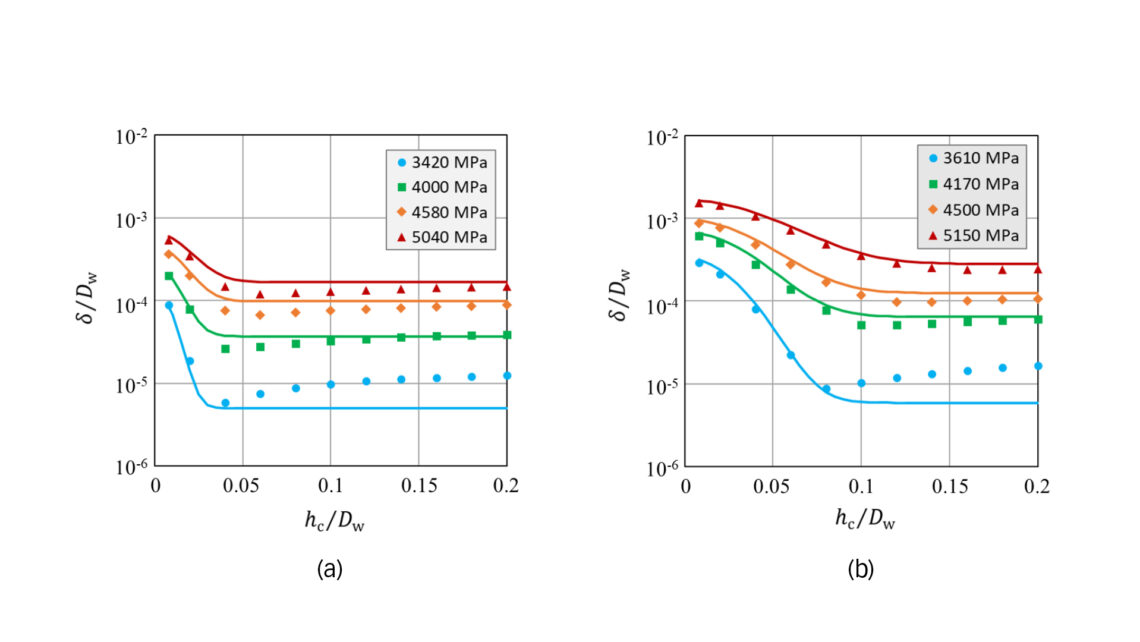
dove p_r è una pressione di riferimento impostata su 1.000 MPa. Le costanti G, u e v si determinano adattando l’equazione (2) e l’equazione (3) ai dati di improntatura plastica ottenuti dai calcoli a elementi finiti, come illustrato in figura 1. Si noti che il coefficiente di carico statico per i cuscinetti sottoposti a tempra passante è definito come la pressione di contatto che corrisponde a una profondità di improntatura plastica superficiale di 10^-4D_w [6].

L’improntatura plastica da contatto ellittico [δ /D_w]_EC risulta dall’interpolazione basata sul rapporto b /a tra i risultati dei contatti puntiformi e lineari:

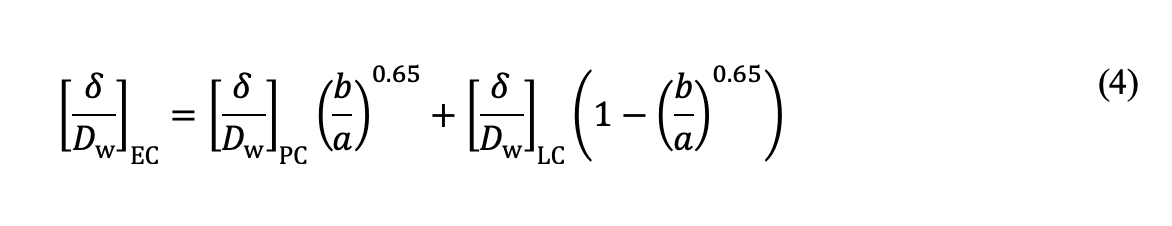
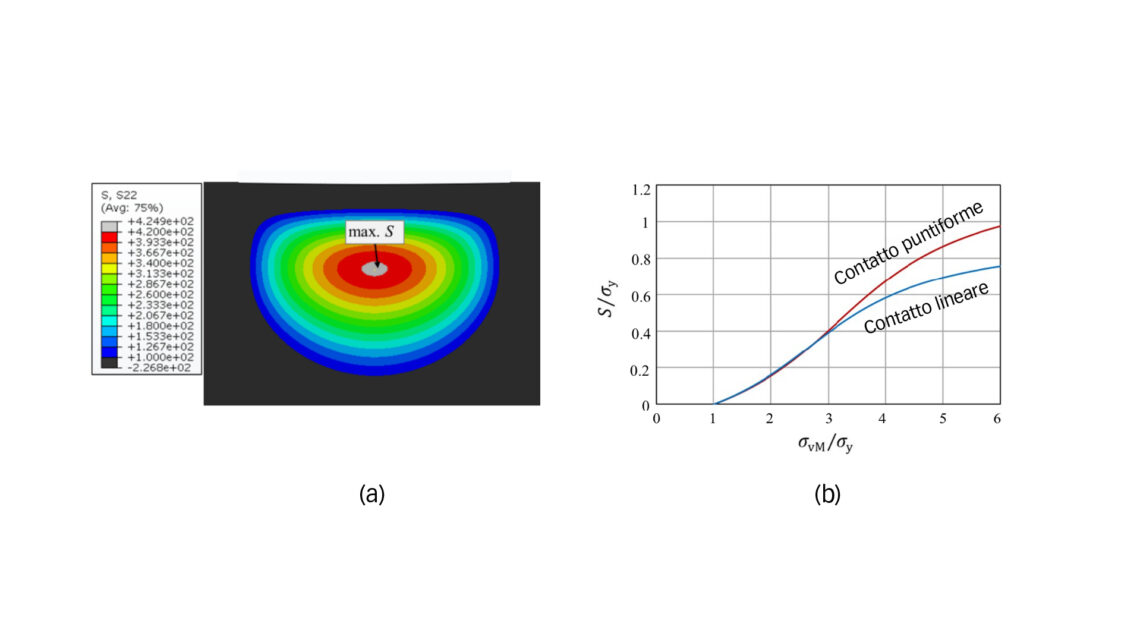
Dall’analisi a elementi finiti esaminiamo la risposta del materiale alle sollecitazioni residue indotte dalla plasticità. Quando le sollecitazioni di un carico statico superano il limite di snervamento del materiale del cuore, si verifica un flusso plastico che porta al danneggiamento del materiale sotto la superficie in forma di sollecitazioni residue. La figura 2a mostra una zona di sollecitazioni di trazione residue nell’area di transizione tra strato cementato e cuore, risultante da sollecitazioni di contatto elevate. Un modello di sollecitazioni residue analogo è stato identificato nei componenti sottoposti a tempra superficiale per induzione soggetti a improntatura con sfere o rulli, come dimostrato in uno studio precedente [5]. Questo studio ha rivelato che in condizioni di carico di fatica da contatto statico, le sollecitazioni di trazione residue possono indurre cricche o delaminazione nell’interfaccia tra strato cementato e cuore.

L’espressione per le sollecitazioni di trazione residue sotto la superficie causate dal carico di contatto statico, come dimostrato in precedenza [5], è applicabile ai componenti cementati:

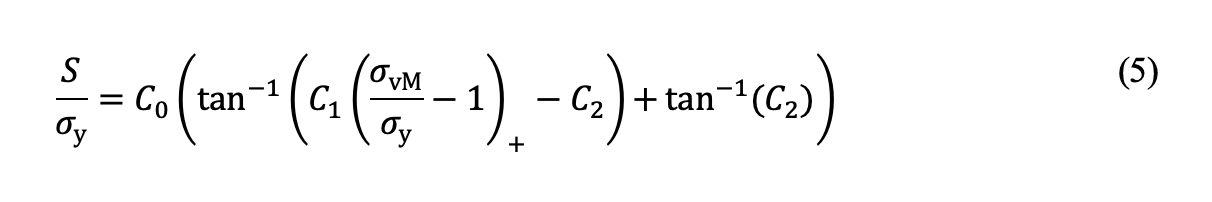
dove σ_y è la resistenza allo snervamento del materiale del cuore, σ_vM indica le sollecitazioni di von Mises equivalenti a una profondità di h_c dalla superficie o la profondità alla quale la durezza è uguale a HV550. C₀, C₁ e C₂ sono costanti, che possono essere determinate adattando l’equazione (5) ai risultati degli elementi finiti. È importante notare che le sollecitazioni di von Mises qui si valutano utilizzando la teoria hertziana del contatto elastico, che rappresenta il risultato delle sollecitazioni nell’ipotesi di elasticità lineare. La figura 2b mostra le sollecitazioni di trazione residue in funzione delle sollecitazioni di von Mises equivalenti a una profondità di h_c dalla superficie, rispettivamente per il contatto lineare e per il contatto puntiforme. Le sollecitazioni critiche, S_c, possono essere valutate utilizzando i principi della meccanica della frattura e l’approccio di El Haddad [8] per considerare gli effetti di cricche di piccole dimensioni, come specificato nel nostro precedente lavoro [5].

Verifica del modello e degli esperimenti

Le prove di fatica da contatto statico sono state condotte su un campione piatto realizzato in ASTM A534-18NiCrMo14-6. Due campioni di disco sono stati sottoposti a cementazione e in seguito a tempra, ottenendo due profili di durezza con profondità dello strato cementato rispettivamente di 0,5 mm e 0,9 mm. Per le prove di fatica da contatto statico è stato utilizzato un rullo bombato con un diametro di 10 mm e un raggio della corona di 98 mm, realizzato in acciaio ASTM A295-52100 temprato a struttura martensitica. Per monitorare le variazioni di deformazione durante le prove, sono stati applicati degli estensimetri all’esterno dell’area dove sono impresse le impronte. Si è dimostrato [4] che un improvviso aumento della deformazione indica l’innesco di una cricca laterale nell’area di transizione tra strato cementato e cuore, che serve come prova del cedimento per schiacciamento del cuore in condizioni di carico di fatica da contatto statico per un componente sottoposto a tempra superficiale.

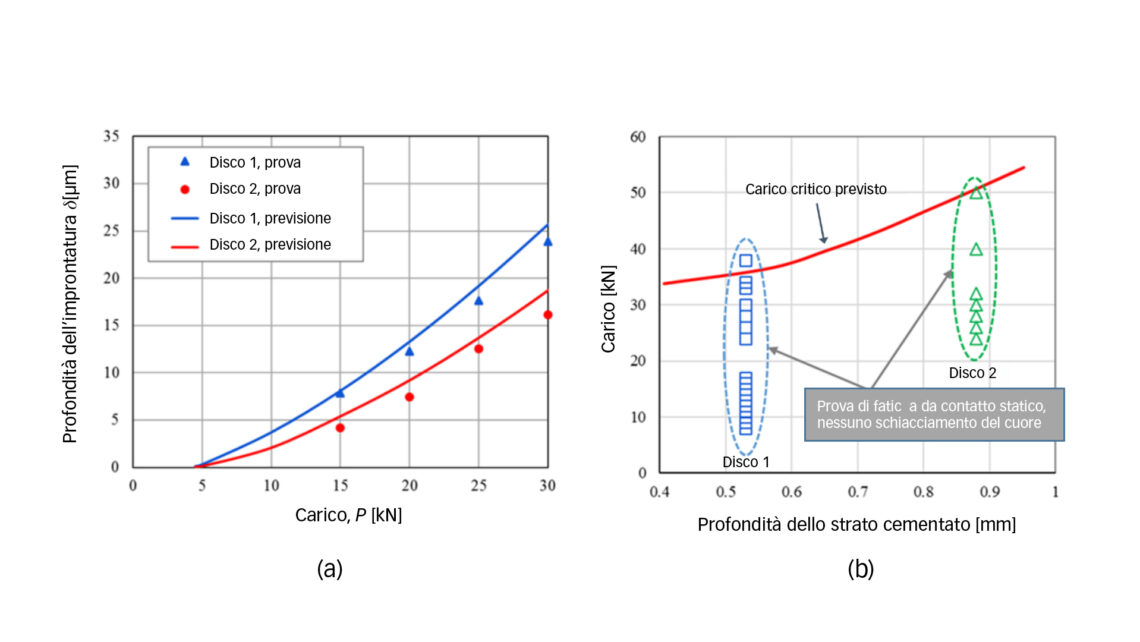
La figura 3a mostra le improntature plastiche misurate rispetto alle previsioni del modello utilizzando le equazioni (1)-(4), che confermano che previsione ed esperimento non presentano discrepanze significative.

Per tutte le prove condotte su entrambi i dischi con carichi diversi, i segnali degli estensimetri non hanno fornito indicazioni di sviluppo di cricche laterali nelle aree sotto la superficie. L’indagine metallografica successiva alle prove ha confermato l’assenza di cricche laterali nelle aree sotto la superficie dei dischi testati. La figura 3b presenta tutte le prove di fatica da contatto statico raggruppate nel disco 1 e nel disco 2, corrispondenti alle due profondità dello strato cementato. Il carico critico per lo schiacciamento del cuore, che indica l’innesco di una cricca laterale sotto la superficie, è stato calcolato e rappresentato nella figura 3b. La previsione del modello è considerata plausibile, perché quasi tutti i punti dei dati sperimentali, che non indicano lo schiacciamento del cuore, sono inferiori ai carichi critici previsti. L’unico dato leggermente superiore al carico critico previsto suggerisce una previsione conservativa del modello. In particolare, le prove di fatica da contatto statico su entrambi i dischi hanno comportato carichi estremamente elevati in termini di pressione di contatto nominale. Ad esempio, il carico massimo sul disco 1 corrisponde a una pressione hertziana di 7,1 GPa, mentre la pressione di contatto massima del disco 2 ha raggiunto i 7,7 GPa. Grazie alle sue proprietà, l’acciaio cementato di questo studio sembra meno suscettibile allo schiacciamento del cuore rispetto ai componenti sottoposti a tempra superficiale per induzione [5].

Prove di improntatura statica sono state eseguite sulla superficie della pista di un cuscinetto a rulli cilindrici. Il campione di prova era un segmento tagliato dall’anello interno del cuscinetto a rulli cilindrici in acciaio ASTM A534-18NiCrMo14-6 cementato e temprato. Per le improntature sono stati utilizzati rulli cilindrici sottoposti a tempra passante di diversi diametri per ottenere condizioni di carico con diverse profondità relative dello strato cementato in termini di rapporto hc/Dw.

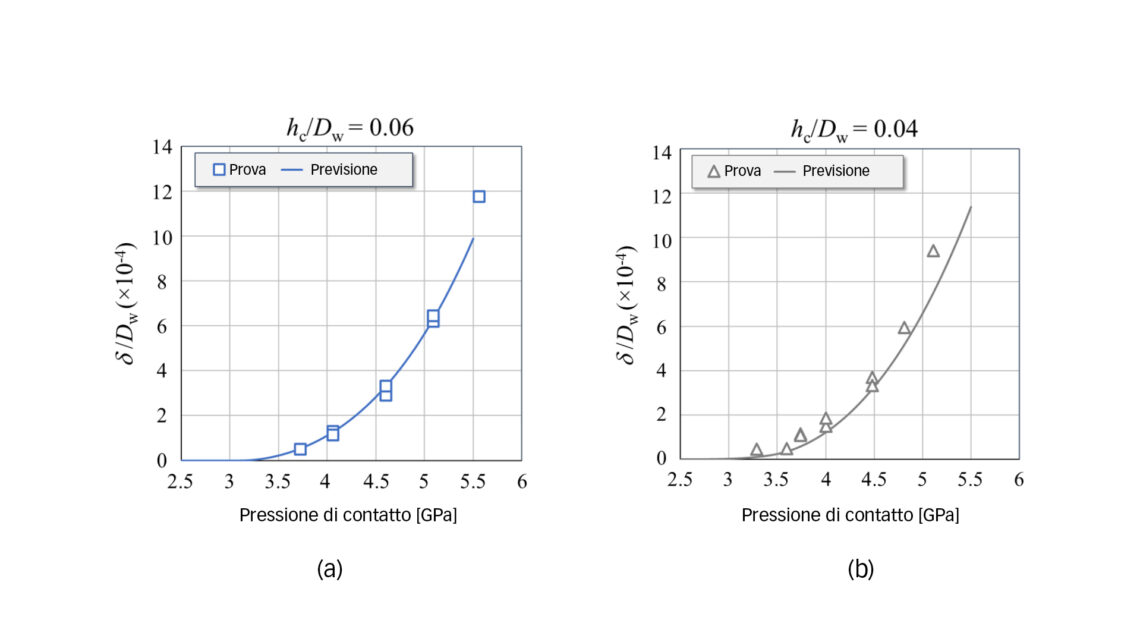
La figura 4 mostra le improntature plastiche per due profondità relative dello strato cementato, ottenute dalla misurazione e dalla previsione utilizzando le equazioni (1)-(4), rispettivamente. Esperimento e previsione del modello non presentano discrepanze significative.

Considerazioni finali

In conclusione, questo studio ha approfondito la risposta dei materiali degli anelli cementati in condizioni di carico di fatica da contatto statico, utilizzando una combinazione di simulazioni numeriche e indagini sperimentali. Concentrandosi sull’improntatura plastica superficiale e sullo schiacciamento del cuore sotto la superficie, i nostri modelli basati su elementi finiti hanno previsto con precisione il comportamento delle deformazioni e dei danneggiamenti dei materiali. La convalida mediante prove di fatica da contatto statico sul blocco e sull’anello interno cementati di un cuscinetto a rulli cilindrici ha confermato l’affidabilità del modello. Questo lavoro non solo favorisce la comprensione, ma offre anche un metodo pratico per valutare le prestazioni dei cuscinetti cementati in condizioni di contatto statico, con possibili implicazioni per l’ottimizzazione della progettazione e della durata nelle applicazioni ingegneristiche.