The estimation of the lubrication quality in rolling bearings of refrigerant compressors has always been a challenge due to many unknowns, e.g., the lubricant dilution by refrigerant, the bearing temperature, the refrigerant piezo-viscosity and viscosity variation with pressure and temperature and the chemical effects of the refrigerant on the bearing raceways. In rolling bearings, the lubrication quality parameter kappa is used. However, even if the effective viscosity of the oil-refrigerant mixture is known in an application, the classical way to calculate the bearing lubrication quality parameter κ, as described in the ISO 281:2007 [1], cannot be applied because this method assumes the lubricating film thickness in the bearing as calculated for an oil. The reduction of the piezo-viscosity in the mixture and the increase of the compressibility with the presence of the refrigerant are not considered. Therefore, in the past several researchers proposed modifications to the original model.

Meyers [2, 3] introduced modifications to the calculation of the lubrication quality parameter κ in rolling bearings to consider the diluted refrigerants in the oil. Then he applied this parameter in the L₁₀ life estimation for rolling bearings. However, no endurance tests were presented to validate the methodology. He also mentions (internal communication) that B.O. Jacobson found that the reduced chlorine of the HCFC-22 refrigerant and the absence of chlorine in the HFC-134a refrigerant significantly increases the viscosity requirements for rolling bearing lubrication. He estimated that two times greater operating viscosity is needed for a bearing lubricated by a mixture of HCFC-22 and mineral oil and three times greater viscosity for a mixture of HFC-134a and polyolester (POE) oil compared with a mineral oil-lubricated bearing. For the first time an engineering safety factor due to refrigerant chemistry (beyond the simple calculation of film thickness) was introduced in the calculation of the bearing’s required viscosity. This model is summarized in Meyers, [2].

While the L₁₀ estimation remains a challenge in this application, it is perhaps an ideal candidate for a bearing life model that explicitly separates the surface from the subsurface, as in Morales-Espejel et al. [4]. However, the methodology suggested in [4] requires a correct film thickness estimation in the contact, which is only possible if the viscosity, piezo-viscosity and compressibility of the mixture can be estimated. Some researchers have tried to develop methodologies for this. Despite the progress, very few publications exist with an engineering methodology for the estimation of oil-refrigerant mixture viscosity, piezo-viscosity, film thickness and required viscosity. The current work describes a methodology to achieve this by independently applying the viscosity variation with the pressure and temperature of the oil and of the refrigerant. Then the lubricating properties of the mixture are calculated with the use of modified mixture law equations. From this, Daniel plots can be reproduced and estimating the bearing required viscosity and lubrication quality parameter is possible.

Mixture laws

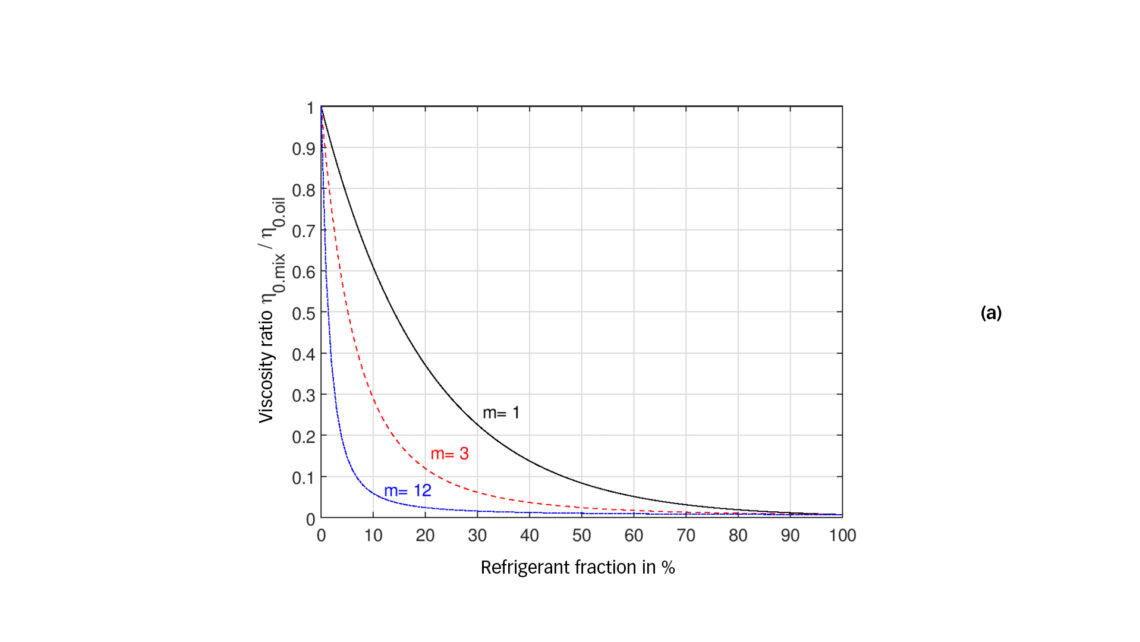
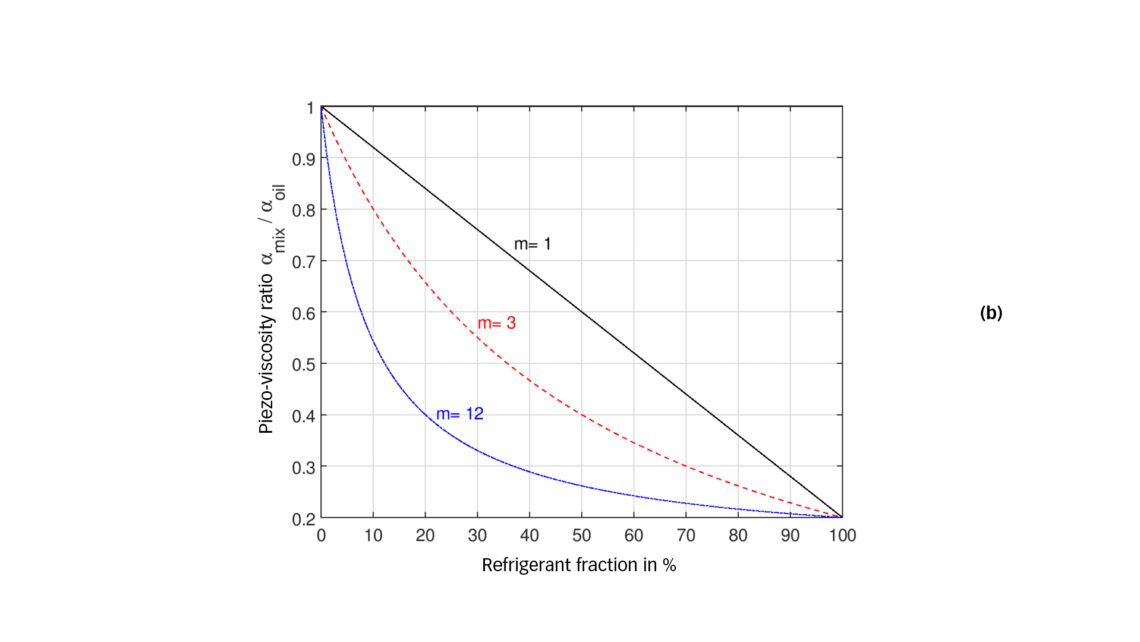
Literature models Studies have been carried out in the past to measure and estimate the film thickness in EHL contacts lubricated with oil-refrigerant mixtures. In calculating film thickness in EHL contacts lubricated with oil-refrigerant mixtures, estimating the mixture properties is a key intermediate step. Diverse equations have been suggested to estimate viscosity and piezo-viscosity of oil-refrigerant mixtures. For example, Akei and Mizuhara [5] use the Eyring theory to derive equations for the piezo-viscosity coefficient and viscosity: 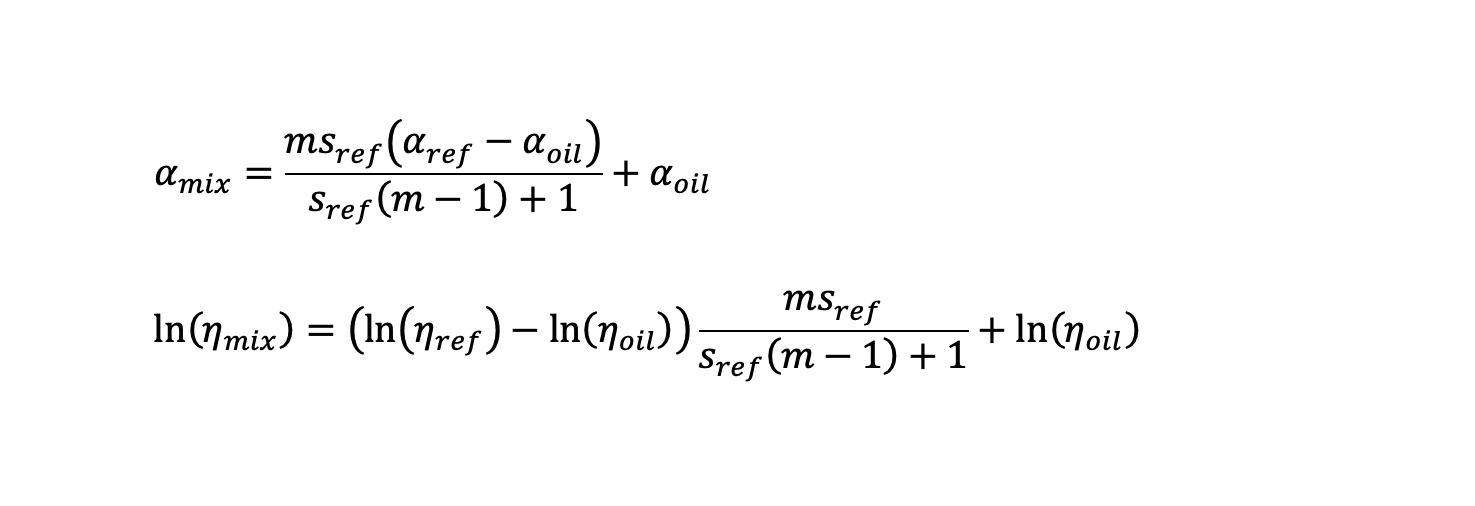Where m=M_oil / M_ref , M being the molecular mass of the component. Here α is the piezo-viscosity coefficient, η is the dynamic viscosity, s is the fraction of the component dilution, oil refers to oil and ref refers to refrigerant. The previous equations can be plotted for different refrigerant fractions and molecular mass ratios, as shown in fig. 1 as illustrative example.

In Morales-Espejel and Hauleitner [6] the predictions of these equations were confronted with different oil-refrigerant mixtures where experimental data exist. The disagreement between the predictions using the above equations together with the molecular mass ratios taken from publications and measurements motivated the modification of the equations to better predict the measurements.

Adapted model

The original mixture equations are modified with two functions (k_al, k_et) multiplying the molecular mass ratio, as follows: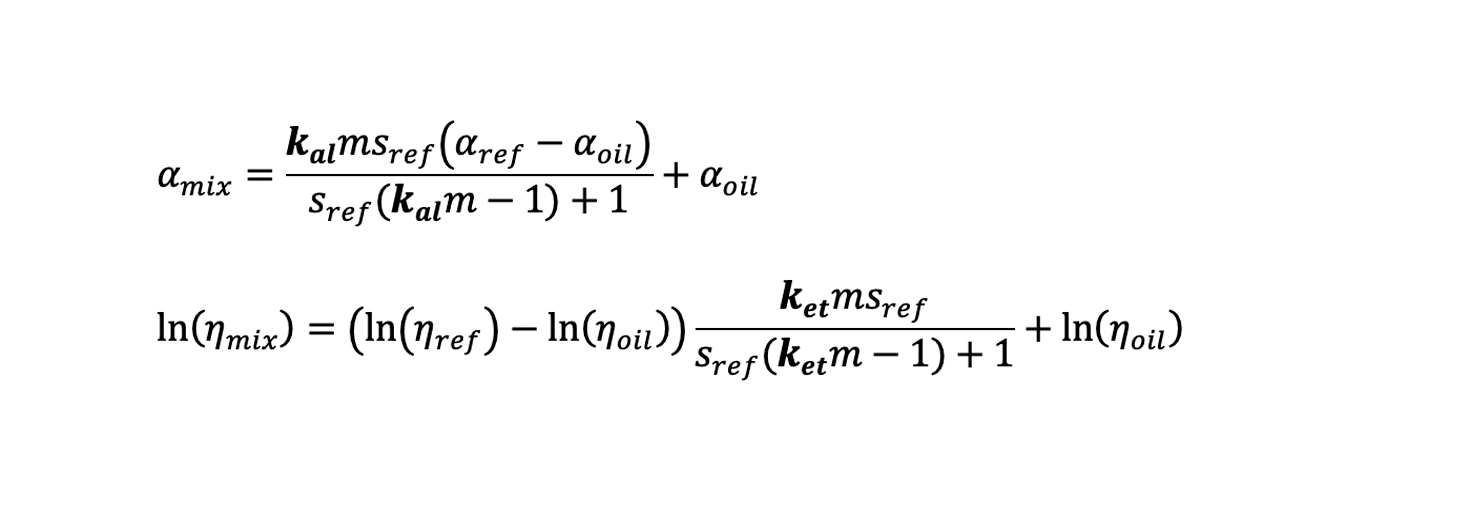

These functions are calibrated using viscosity measurements of different oil-refrigerant mixtures, so these functions depend on the oil viscosity and working temperature. Thus,

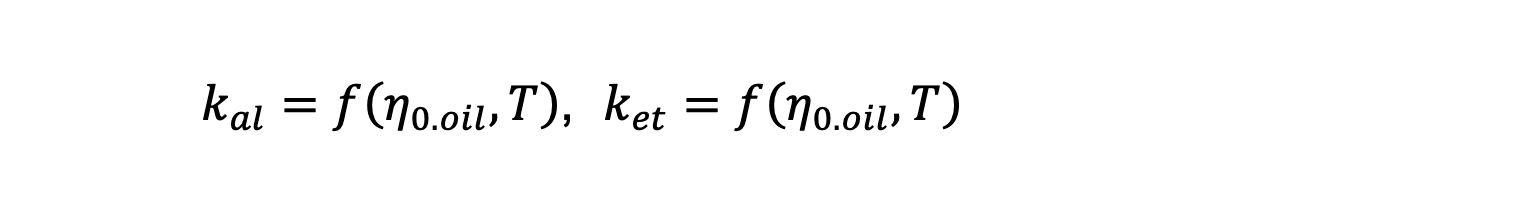
where, η₀ is the dynamic viscosity of the oil at atmospheric pressure and T is temperature.

In [6] it was shown that with the improved model a much better agreement with measurements of a mixture of refrigerant HFC-134a and POE 100 oil could be obtained. The model was tested with several other combinations of oils and refrigerants at different temperatures and dilutions, and the agreement with measurements was always much better than the original model.

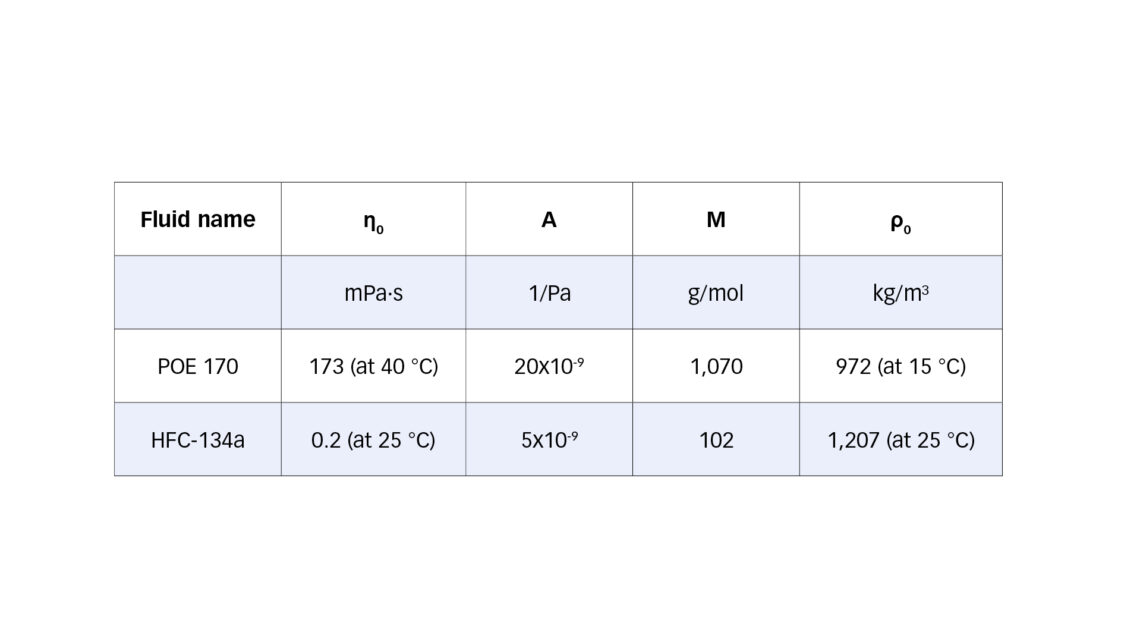
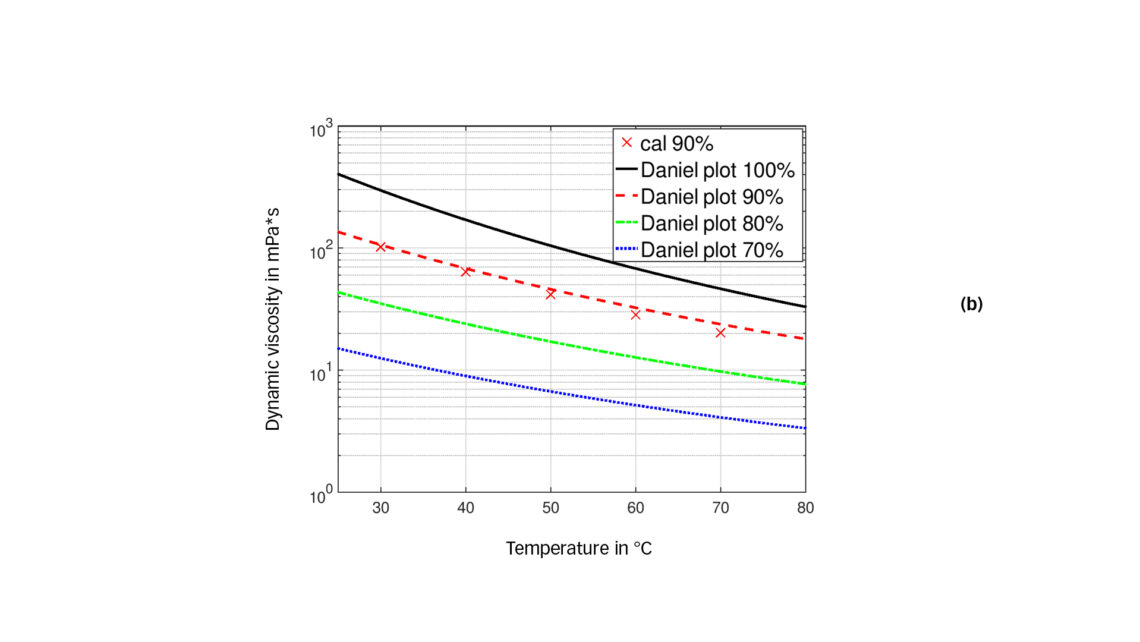
In this work the described approach is applied to the mixture of refrigerant HFC-134a and POE 170 oil, a typical combination used in refrigerant screw compressors (Fuchs Schmierstoffe GmbH [7]). The considered fluid properties are summarized in table 1. The Daniel plot for this mixture is shown in fig. 2 and was published in the brochure Fuchs Schmierstoffe GmbH [8].

Following the approach above allows reproduction of the curves of the Daniel plot based on the properties of the individual fluids. In this example, the data from table 1 is used to reproduce the viscosity of the POE 170 oil with 10 % of refrigerant HFC-134a. Fig. 3 shows a good agreement between the calculated data with the data from the Daniel plot.

Lubrication quality in rolling bearings

For the lubrication quality parameter κ of rolling bearings lubricated with a mixture of oil and refrigerant, a modification is proposed in [6]. The final adjusted actual viscosity of an oil-refrigerant mixture for kappa calculation (κ=ν_adj ⁄ ν₁) , where the adjusted viscosity is: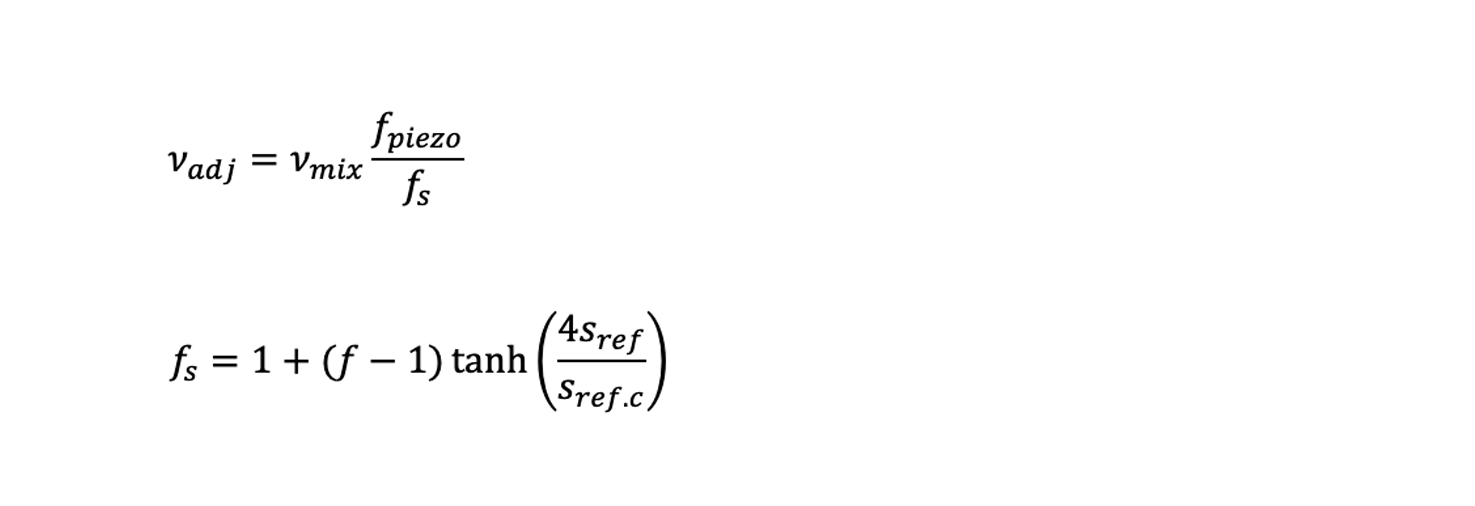

And,

 

 

Notice that mathematically the adjustment factor f_{adj =} f_piezo / f_s has no limit and can reach mixture rates of 100 % refrigerant, but of course all-steel bearings will not survive this, as discussed in [10]. Therefore, it is proposed to limit this compensation technique for practical reasons to a maximum dilution of 30 % refrigerant (s_ref <0.3).

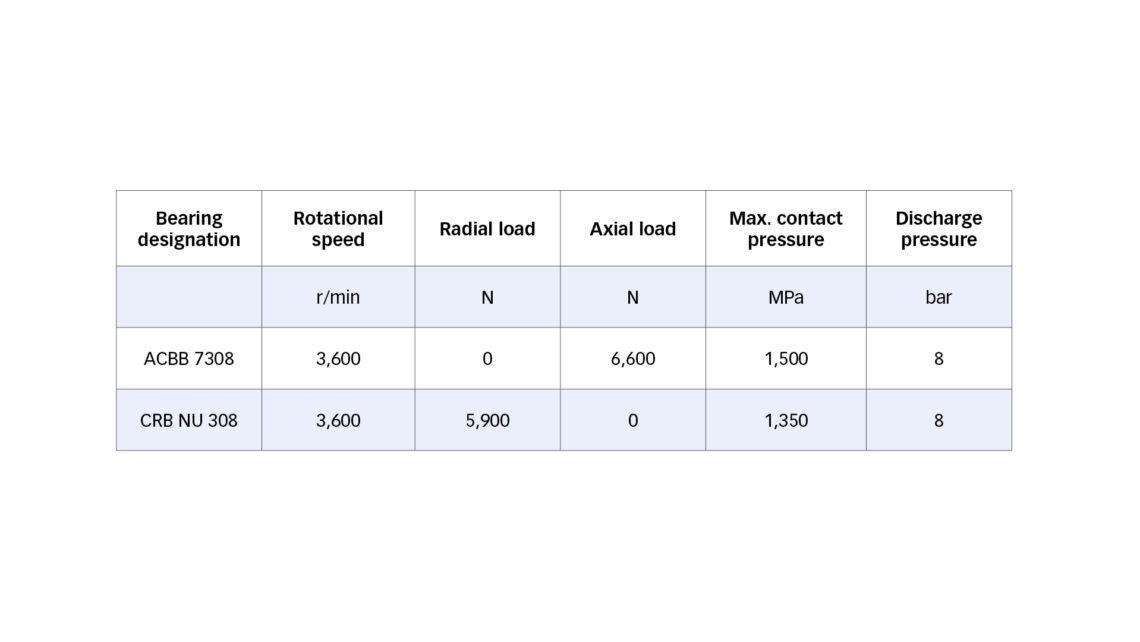
In the following, we consider a practical application example and demonstrate the potential of the described methodology and the effect of lubricant viscosity behaviour for system calculations. The lubrication quality of bearings in a screw compressor of air conditioning equipment is analysed. Table 2 summarizes the operating conditions.

While in the previous sections the behaviour of the fluid properties is investigated against one changing input parameter only, e.g., mixture viscosity versus dilution in fig. 1 or versus temperature in fig. 2 (b), we want to exemplify how the combined influence of several parameters could affect the lubrication quality of bearings in reality. For this, certain relationships between input parameters are assumed, as explained next.

Influence of temperature and dilution

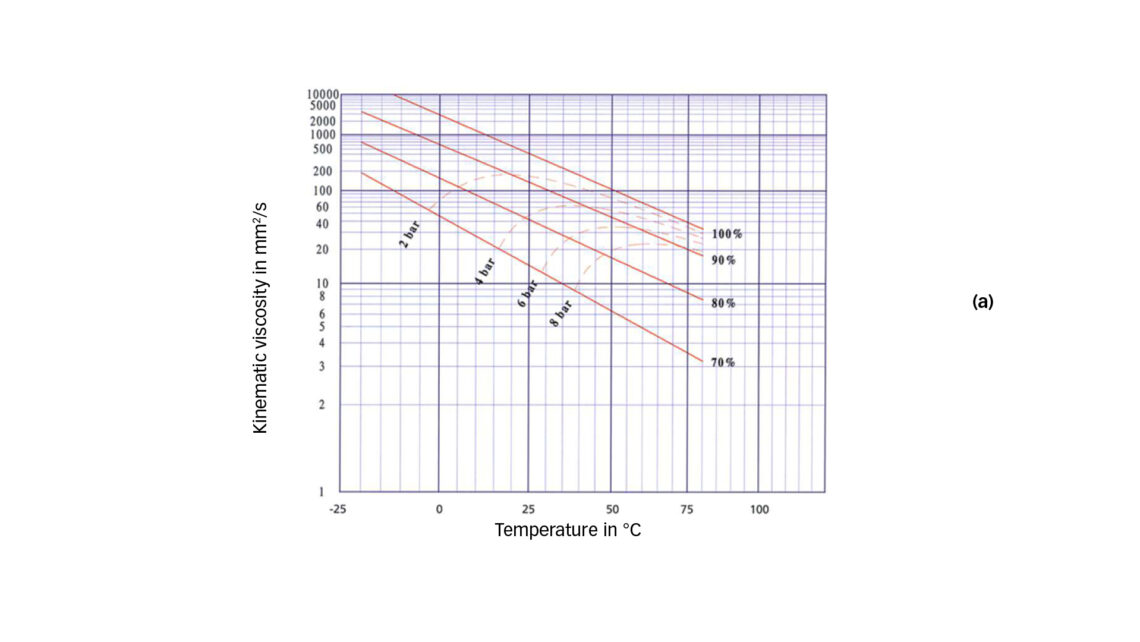
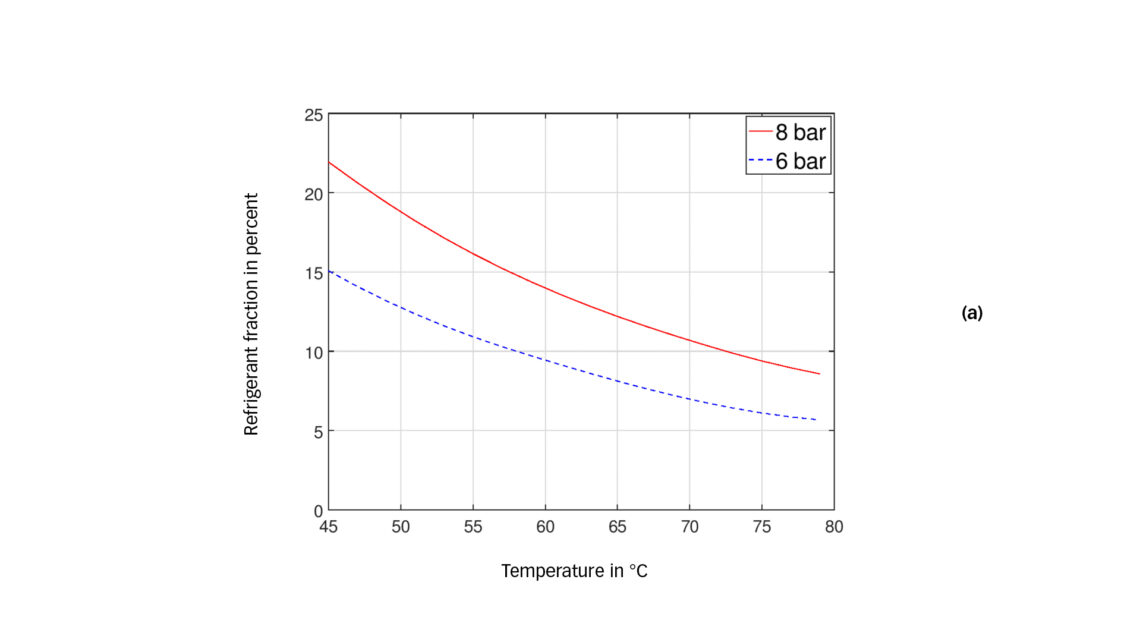
The characteristics of the dilution versus pressure and temperature is specific for each oil-refrigerant mixture, and this information is included in the Daniel plots. In this example, we will assume that the lubricant conditions are determined by the discharge pressure of the compressor. The resulting oil-refrigerant mixture ratio is defined in the Daniel plot by the intersection of the pressure line (isobar lines) and the temperature. In fig. 3 (a), this information is extracted for two pressures from the Daniel plot given in fig. 2 (a). For the mixture of POE 170 and HFC-134a, the dilution of the oil by refrigerant at 6 and 8 bar reduces with higher temperature. In the observed temperature range and at 8 bar, the mixture contains between 8 % and 22 % of refrigerant.

The dilution at a given pressure and temperature is an important factor influencing the lubrication quality of the bearing and depends on the actual combination of oil and refrigerant. The refrigerants with low global warming potential (GWP) and zero ozone depletion potential (ODP) often lead to higher dilutions compared with the previous refrigerant generation, such as HFC-134a.

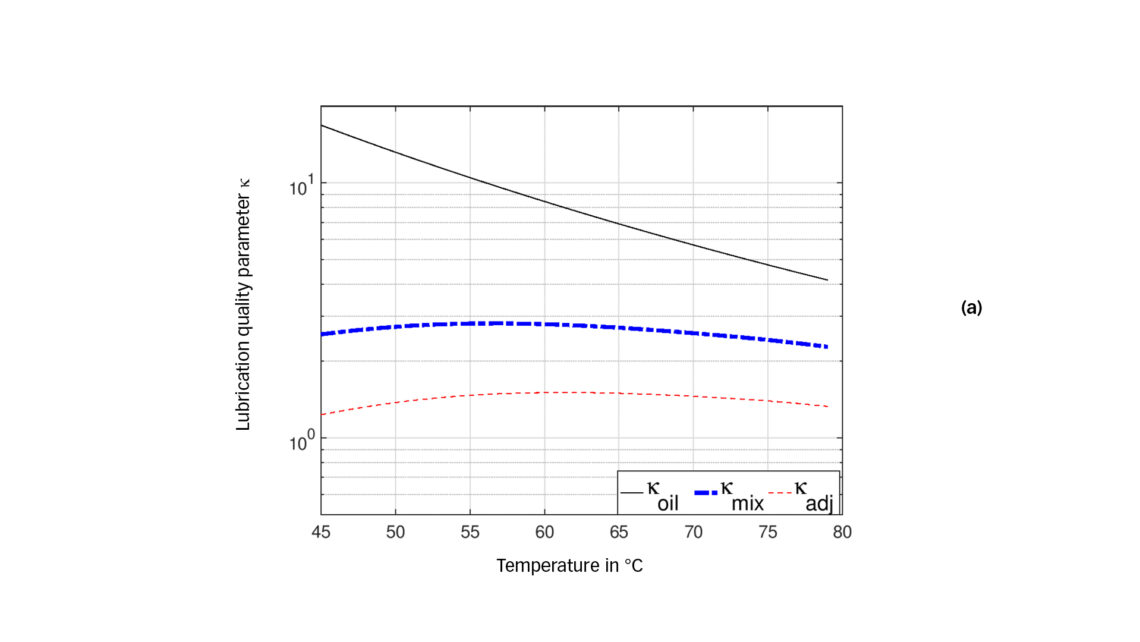
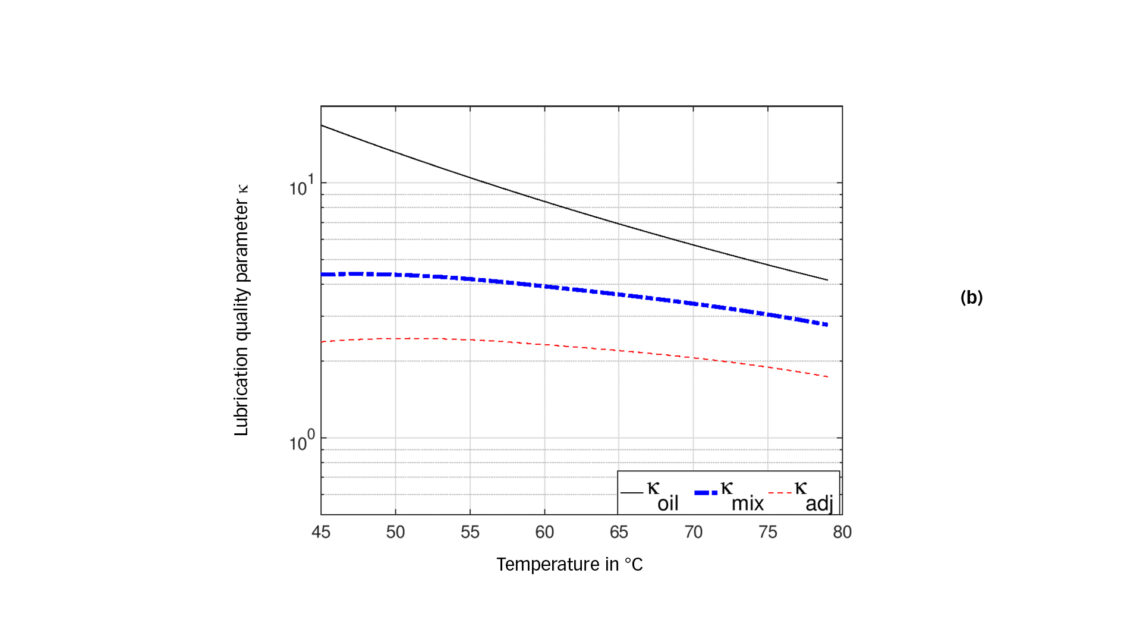
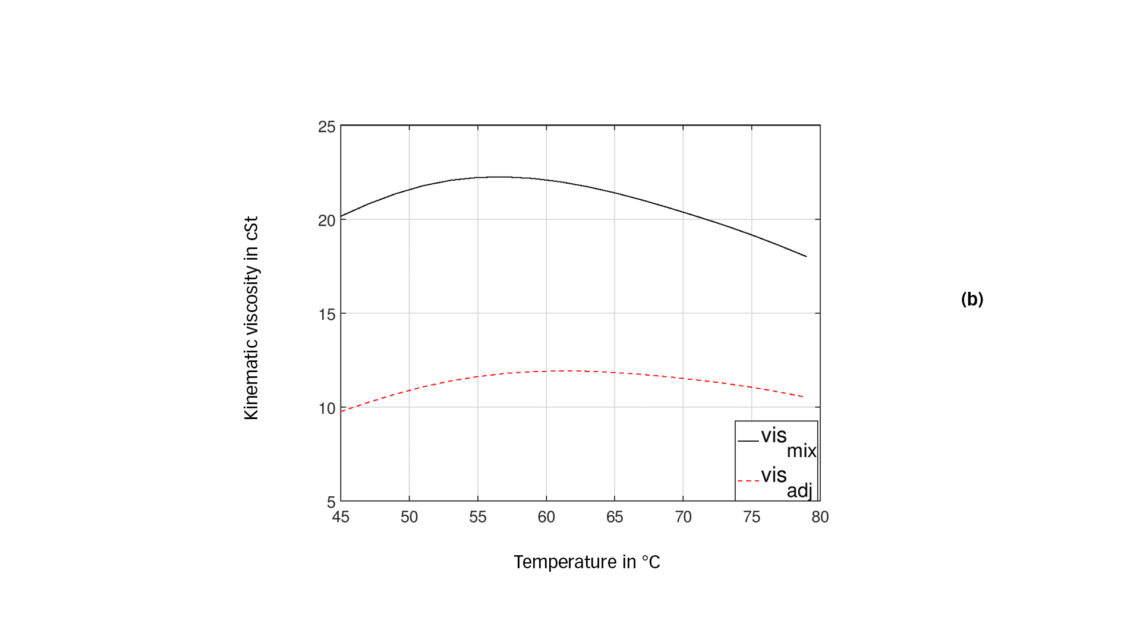
Since mixture viscosity (as well as piezo-viscosity) drops with higher dilution (see fig. 1) and viscosity reduces with higher temperature (see fig. 2(a)), following the characteristic of dilution and temperature from fig. 3 (a) will lead to a superposition of these two opposing trends. This leads to an interesting characteristic forming a maximum viscosity value within the considered temperature range and a drop of viscosity towards lower as well as higher temperatures. This effect is also shown in the Daniel plot when following the isobar line. Fig. 3 (b) shows the reproduction of the mixture viscosity ν_mix at 8 bar according to the adapted equation for the viscosity mixture as well as the adjusted (mixture) viscosity ν_adj, including the reduction of viscosity resulting from the piezo-viscosity effect and the proposed safety factor. Throughout this example, a Jacobson safety factor f equal to 1.5 is used.

Since the results for the lubrication quality parameter for the angular contact ball bearing (ACBB) and the cylindrical roller bearing (CRB) under the chosen operating conditions are very similar, the following graphs only represent the ACBB results.

With the bearing operating conditions from table 2, the lubrication quality parameter is calculated according to the equation for the adjusted viscosity. The results in fig. 4 (a) show that the lubrication quality significantly reduces from the pure oil to the mixture and that the described additional effects (piezo-viscosity, safety factor) lead to a further severe reduction in kappa (graph is plotted on a logarithmic scale). The adjusted kappa is smaller by approximately a factor of 2 than the one obtained with mixture viscosity (given by common Daniel plots). While for lubrication with pure oil, a higher temperature leads to a reduction in kappa, the behaviour for an oil-refrigerant mixture indicates challenging lubrication conditions at the lower and the higher end of the observed temperature range. At the lower end of the temperature axis with increasing temperature the effect of dilution reduction (see fig. 3 (a)) dominates, so kappa increases. At the higher temperature end increasing temperature reduces the viscosity of the heavily oil-charged mixture, so kappa is reduced.

Influence of discharge pressure

Next we repeat the same evaluation but assume a discharge pressure of 6 bar instead of 8 bar (keeping the same rotational speed as before). Fig. 3 (a) shows the reduction in dilution due to the lower pressure. Within the observed temperature range, the refrigerant content is between 6 % and 15 % at 6 bar.

Fig. 4 (b) displays the lubrication quality for the conditions at 6 bar. As indicated by the Daniel plot, the lower pressure results in a lower dilution at the same temperature and, therefore, increases mixture viscosity as well as kappa compared with the 8 bar case.

Influence of rotational speed

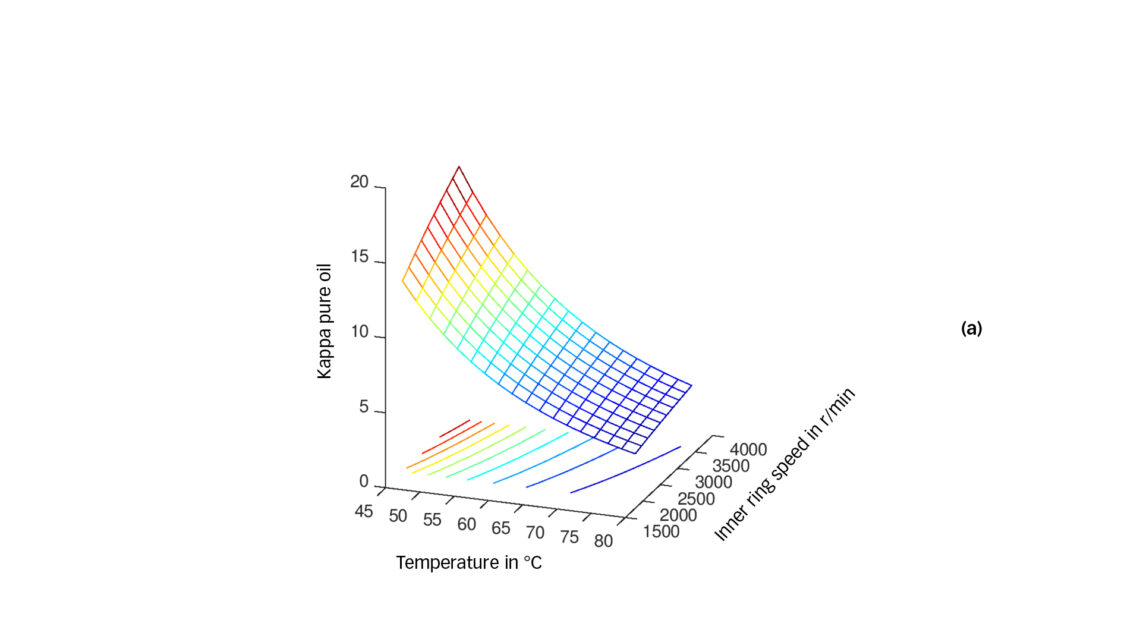
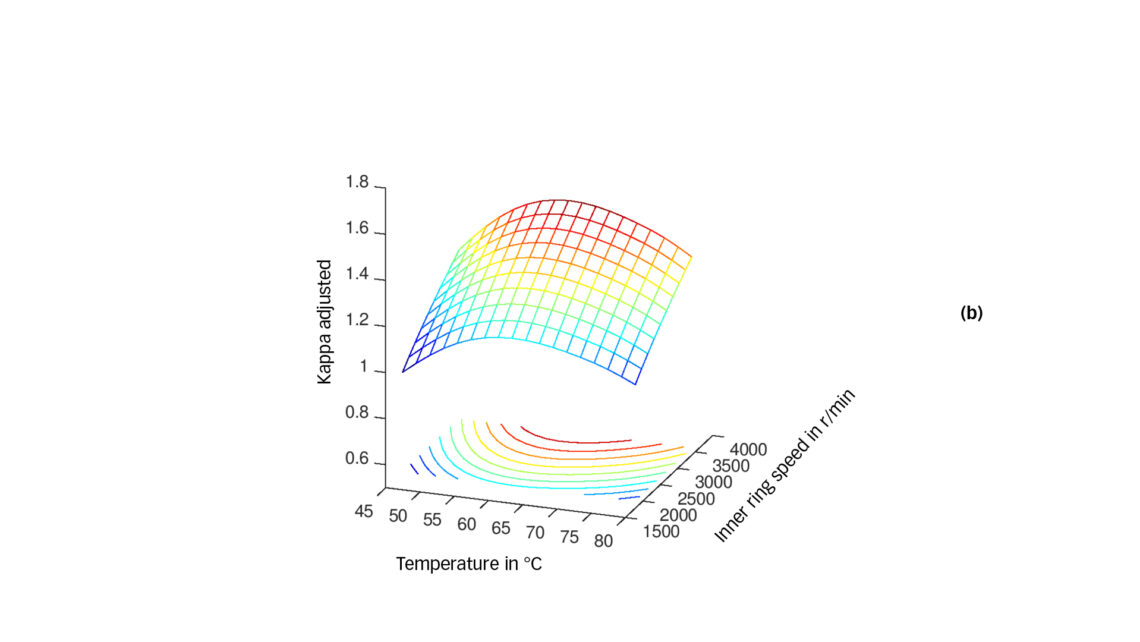
With the introduction of variable speed drives (VSD), an additional dimension in the operating range is the compressor rotational speed. The speed is an important parameter for the film thickness in the rolling element bearing. We resume the condition of before and plot the data with the additional dimension of speed.

Fig. 5 compares the characteristics of the lubrication quality parameter of a pure oil (although having an unrealistic high viscosity for the given conditions) against an oil-refrigerant mixture. For the case of pure oil, the regime with lowest lubrication quality is located at high temperature and low speed. The case of oil-refrigerant mixture shows significantly lower kappa values and different characteristics. There are two areas with the lowest lubrication quality, which are both in the low speed range – the first in in the low and the second in the high temperature region of the observed range. This explains why most of the time the critical bearing position in terms of lubrication quality is on the female – slower rotating – rotor of the twin screw compressor. Ultimately, the effect of reduced speed should be superimposed with the one for reduced discharge pressure.

Conclusions

A complete methodology for estimating the rolling bearing lubrication quality parameter κ has been described. Firstly, accurate mixing law equations for viscosity and piezo-viscosity are developed. With these equations, the corresponding Daniel plots can be derived if not available. Then these equations are used to estimate the viscosity of the mixture. The methodology derives an adjustment factor for the actual viscosity in the bearing when a mixture of oil and refrigerant is present. This adjustment factor when multiplied with the oil-calculated-method mixture viscosity will reduce its value to a safe level.

As shown in this work, the Jacobson safety factor f leaves some freedom to the engineer to adapt the safety of the pursued design, since there are still several unknown effects. One of them already discussed in [10] is the chemical aggressiveness of the refrigerant towards the bearing steel, reducing its fatigue strength due to corrosion or poor lubricity. For example, refrigerants with very low global warming potential (GWP) and zero ozone depletion potential (ODP) might be considered as highly reactive/corrosive fluids, especially with the presence of moisture. In those cases, engineers are encouraged to use f≥2, otherwise 1.5≤f≤2 would be sufficient.

For a real application, all parameters influencing the lubrication quality of the mixture (e.g., temperature, pressure, rotational speed) will be interrelated by the operating cycle of the air conditioning unit. Following the proposed approach, it is possible to predict the lubrication quality for the bearings for each point within the operating map.

From this analysis, the following conclusions can be drawn:

1. The oil-refrigerant mixture law equations found in literature need some adaptation functions dependent on lubricant viscosity and temperature to be accurate in the prediction of mixture viscosity and piezo-viscosity.
2. The oil-calculated-method mixture viscosity in a rolling bearing still needs to be adjusted for piezo-viscosity and safety before it can be used to calculate the lubrication quality of a bearing working in oil-refrigerant conditions.
3. The Jacobson safety factor is an adaptable variable for the design of an application. Highly reactive refrigerants (especially in the presence of moisture) will require larger values of this safety factor.