Зубчатые передачи — это контактные элементы оборудования, проблемы эксплуатации которых во многом схожи с проблемами подшипников качения. Но между ними есть и важные различия. Во многих областях применения подшипники качения и зубчатые передачи работают в тесном взаимодействии. Инженерам, занимающимся подшипниками качения, часто необходимо иметь базовое понимание условий эксплуатации зубчатых передач, поскольку они могут влиять на рабочие характеристики подшипников. Однако методы расчёта ресурса зубчатых передач и подшипников существенно различаются, несмотря на схожесть трибологических факторов. В данной статье рассматривается, как хорошо изученные факторы, влияющие на срок службы рабочих поверхностей подшипников, могут применяться к зубчатым передачам. Кроме того, исследуется новый метод поверхностной и подповерхностной интеграции для расчёта ресурса подшипников и его возможное использование для зубчатых передач. Это впервые позволило бы проводить расчёты ресурса для подшипников качения и зубчатых передач по единой методологии.

Трибологические условия на боковых поверхностях зубьев шестерён идентичны условиям на контактных поверхностях подшипников качения, однако определяющие эти условия параметры различаются по величине. На поверхностях обоих типов наблюдается качение и скольжение (у подшипников скольжение присутствует в значительно меньшей степени, чем у зубчатых передач). Оба типа поверхностей подвержены воздействию высокого давления (у подшипников выше, чем у зубчатых передач). Кроме того, степень шероховатости поверхностей обоих типов сопоставима с толщиной плёнки смазочного материала. Всё это указывает на возможность использования схожих методов для расчёта срока службы контактных поверхностей зубчатых передач и поверхностей качения подшипников. Хорошим примером в данном случае является модель поверхностного разрушения SKF [1], изначально разработанная для подшипников качения и впоследствии использованная для зубчатых передач [2].

В настоящее время номинальные ресурсы зубчатых передач и подшипников качения рассчитываются разными способами. Методики выбора и проектирования зубчатых передач в целом основаны на уравнении Льюиса [3] для изгиба балок. Стандарт AGMA [4] вводит в уравнение Льюиса дополнительные коэффициенты запаса для учёта концентрации напряжений у основания зубьев, а также распределения на зубьях нагрузки и перенапряжений. Помимо сопротивления усталости в зоне у основания зубьев, стандарт AGMA предусматривает проверку максимального напряжения, возникающего у поверхности в области контакта зубьев.

AGMA вводит уравнение для усталостной прочности поверхности, основываясь на «сухих» контактных напряжениях. При этом считается, что если контактное напряжение превышает определённую критическую величину, то это приведёт к выкрашиванию зубьев. Такие методики успешно использовались в течение нескольких последних десятилетий для проектирования и определения размера зубчатых передач. Однако в связи с растущими запросами со стороны промышленности на уменьшение размеров компонентов оборудования, снижение энергопотребления и производственных затрат инженеры постоянно ищут более современные способы оптимизации размеров механических компонентов.

Новейшие знания в области трибологии, автоматического смазывания, технологий обработки поверхности и контроля чистоты могут внести существенный вклад в повышение надёжности зубчатых передач. Это может открыть новые возможности для повышения механической эффективности и устранения избыточности при проектировании. Сегодня в организациях, занимающихся стандартизацией зубчатых передач, предпринимаются значительные усилия по оценке риска микровыкрашивания (образования микрораковин) [5], что свидетельствует о важности этой темы применительно к надёжности зубчатых передач. Однако до настоящего времени трибологические факторы (риск так называемого микровыкрашивания) могут учитываться в процессе проектирования зубчатых передач лишь косвенно. При этом в отличие от подхода, используемого для подшипников качения, не даётся никаких конкретных указаний в отношении ожидаемого срока службы зубчатых передач.

В то же время для подшипников качения на протяжении многих лет использовались уникальные специализированные способы моделирования для прогнозирования ожидаемого усталостного ресурса контакта качения в зависимости от условий эксплуатации. К наиболее важным из них относятся:

• применение теории наислабейшего звена Вейбулла в рамках дисциплины сопротивления материалов [6], где учитывается сопряжённый с риском уровень напряжения материала;
• теория динамической грузоподъёмности Лундберга-Палмгрена [7–8];
• статистический способ определения усталостной прочности, т. е. надёжности в 90 % для срока службы L₁₀;
• критерий усталостного напряжения Иоаннидиса-Харриса [9], позволяющий учитывать влияние качества смазывания и чистоты смазочного материала на усталостный ресурс контакта качения.

Кроме того, совсем недавно был представлен новый общий подход к усталостному ресурсу контакта качения — так называемая обобщённая модель для расчёта ресурса подшипника (GBLM) [статья в журнале SKF Evolution № 4 за 2015 год]. В рамках этого нового метода поверхностные повреждения напрямую учитываются в базовых формулах расчёта усталости в зоне контакта качения. Он рассматривает вероятность безотказной работы поверхности как риск отказа, который не зависит от подповерхностных напряжений по Герцу [10–11]. Это открывает новые возможности использования специализированных трибологических моделей для описания поверхностных отказов в зоне контакта качения.

Для зубчатых передач такие концепции моделирования пока не применялись. При проектировании зубчатых передач использование срока службы L₁₀ и номинальной динамической грузоподъёмности не получило широкого распространения, несмотря на значительные усилия в 1970-х годах, инициированные новаторской работой Коя и соавторов [12–15].

Целью данной работы является краткое обсуждение способов адаптации модели [10] и изучение возможности её применения для зубчатых передач. Основная концепция представлена на рис. 1. Области возникновения напряжений на поверхности и в подповерхностном слое зубчатой передачи в зоне контакта анализируются отдельно с учётом их влияния на безотказную работу зубчатого зацепления, однако при оценке L₁₀ они учитываются вместе.

Увеличенное изображение показывает распределение контактного давления, а также поверхностные и подповерхностные напряжения в зоне контакта. Поверхностные напряжения в основном определяются микрогеометрией контактных поверхностей зубьев зубчатой передачи.

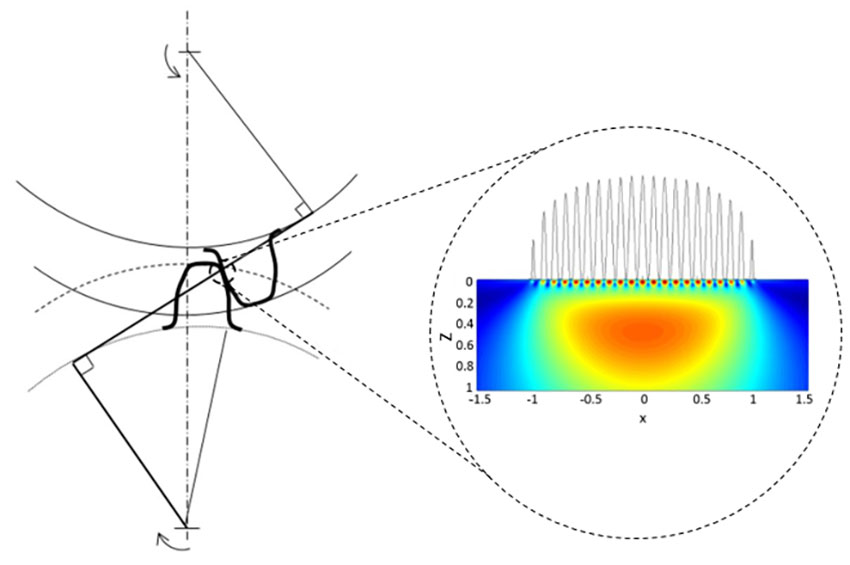
Будет полезно проиллюстрировать преимущества предлагаемого метода оценки ресурса по сравнению с другими, используемыми в настоящее время, а также показать те возможности, которые открывает более комплексный подход к расчёту срока службы контактных поверхностей зубчатых передач.

Трибологические условия для подшипников качения и зубчатых передач

На рис. 2 приведено сравнение типичных трибологических условий для зубчатых передач и подшипников. Можно увидеть, что в целом условия в подшипнике качения кажутся более сложными, чем в зубчатых передачах, с более высокими значениями давления, более длительными требуемыми сроками службы и меньшими толщинами смазочной плёнки. Однако у зубчатых передач скольжение присутствует в большей степени, и они имеют более высокую шероховатость, что не способствует увеличению ресурса поверхностей. Помимо этого, у зубчатых передач направление неровностей поверхности обычно идёт перпендикулярно направлению качения/скольжения, в отличие от подшипников качения, у которых направление шероховатости идёт вдоль направления качения. В условиях смешанного смазывания это может быть преимуществом для подшипников.

Срок службы подверженных воздействию трения поверхностей зубчатых передач и подшипников качения в основном определяется двумя важными факторами: качеством смазывания и степенью загрязнения твёрдыми частицами. При этом оба аспекта учитываются в общем расчёте ресурса подшипников качения (ISO 281), но не учитываются полностью в существующей модели расчёта ресурса зубчатых передач. Однако недавно разработанная концепция учёта вероятности безотказной работы поверхности как риска отказа, который не зависит от подповерхностных напряжений по Герцу (обобщённая модель для расчёта ресурса подшипника), способна не только помочь учитывать для зубчатых передач те же поверхностные факторы, что и для подшипников качения, но и окончательно унифицировать методики расчёта.

Поверхностные разрушения зубчатых передачs

Поверхности зубчатых передач, как и подшипников, могут разрушаться (это явление также называется микровыкрашиванием или серым окрашиванием) в условиях неправильного смазывания. Это может произойти в случае использования масла со слишком низкой вязкостью, при слишком большой шероховатости поверхностей зубчатой передачи и в условиях низких частот вращения. Другими словами — при низком качестве смазывания или низком коэффициенте Λ.

Поверхностные разрушения являются следствием поверхностной усталости на уровне неровностей, которые могут быть компенсированы умеренным износом [1–2]. Достаточный умеренный износ может убрать вершины неровностей и локально снизить давление, что способствует уменьшению поверхностных разрушений и усталости. Умеренный износ также может способствовать удалению слоёв материала, претерпевших усталостный износ.

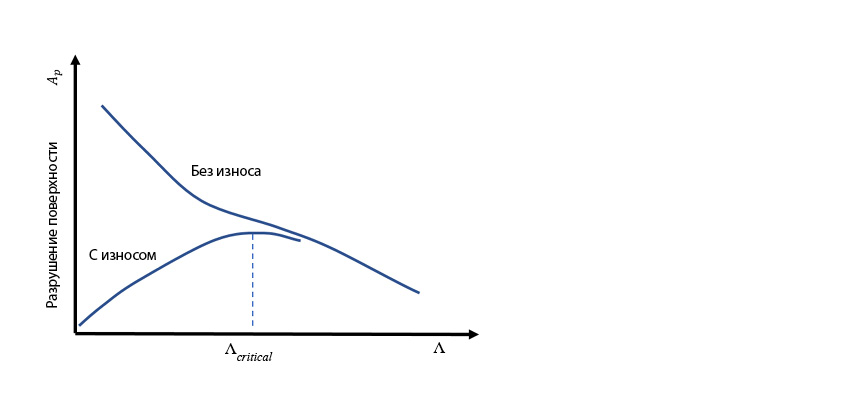
Слишком низкий умеренный износ может продлить период приработки поверхностей, вызывая больше повреждений и более серьёзные поверхностные разрушения. С учётом этого более низкие значения Λ могут привести к меньшим поверхностным разрушениям вследствие увеличения износа. В противном случае поверхностные разрушения должны увеличиваться. Это проиллюстрировано на рис. 3.

Другим важным фактором поверхностного разрушения зубчатых передач является наличие условий для так называемого отрицательного проскальзывания применительно к поверхности, движущейся медленнее. Нередко отмечается, что такая более медленная поверхность больше подвержена поверхностным разрушениям по сравнению с той, что движется быстрее. Это явление было объяснено в работе [2], где показано, что более медленная поверхность проходит через большее количество микроциклов усталости, вызванных шероховатостью более быстрой поверхности, помимо потенциальных эффектов растрескивания поверхности и более интенсивного распространения трещин.

Ресурс зубчатых передач с учётом безотказной работы поверхности и подповерхностного слоя

Полное описание предлагаемой модели представлено в работе [16], здесь же важно привести итоговое уравнение для ресурса:

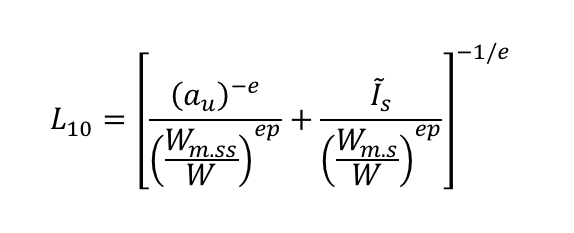
Где:

Это уравнение ресурса (1) содержит два основных члена. Первый (слева) относится только к подповерхностному слою, где могут быть использованы классические уравнения по Герцу. Второй (справа) относится только к поверхностному слою, где для оценки поверхностных повреждений используются более сложные трибологические модели [1]. В данном уравнении используется та же методика расчёта, что и в обобщённой модели для расчёта ресурса подшипников качения.

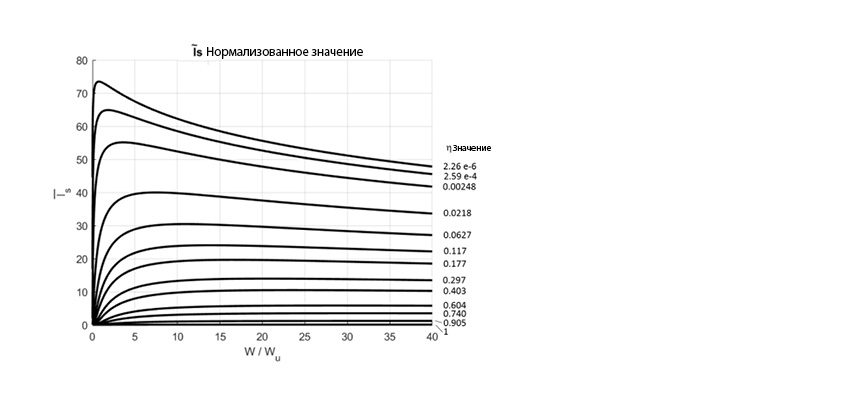
Уравнения динамической грузоподъёмности зубчатых передач (для подповерхностного слоя) W_m.ss были даны ранее в работе Коя с соавторами [12–15]. Уравнение динамической грузоподъёмности (для поверхности) W_m.s представлено в работе [16]. Следует отметить, что в отличие от подшипников, в данном уравнении дополнительно введена динамическая грузоподъёмность для поверхности. В случае с подшипниками аналогом было бы введение величины «С» также и для поверхности.

Рис. 4. Пример использованной выше нормализованной величины Ĩ_s, где η — коэффициент окружающей среды η=η_b η_c (как для подшипников).

Пример применения

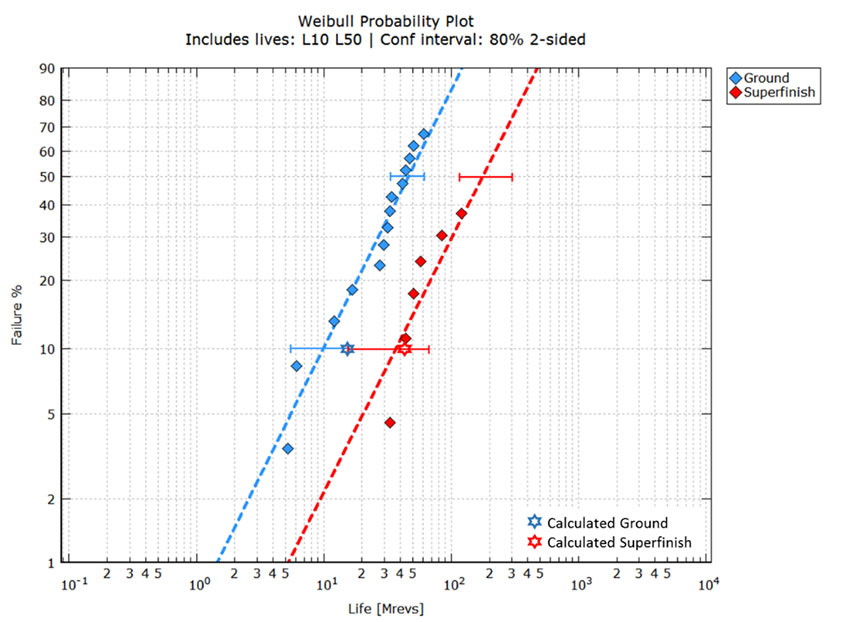
В работе [17] сравниваются ресурсы прямозубых зубчатых передач двух групп: одной — просто со шлифованными поверхностями, другой — с прецизионно обработанными поверхностями. Там же приведены все данные зубчатых передач, сведения о материалах, геометрии и условиях эксплуатации. Для обеих групп проведены испытания при одинаковых условиях эксплуатации за одним исключением: состояние группы зубчатых передач со шлифованными поверхностями ухудшается при низком коэффициенте Λ вследствие более высокой шероховатости (Λ≈1.13), а зубчатые передачи с прецизионно обработанными поверхностями позволяют обеспечить более качественное смазывание благодаря меньшей шероховатости (Λ≈6.17). Представленные в работе [17] результаты испытаний для зубчатых передач со шлифованными поверхностями и с прецизионно обработанными поверхностями были оцифрованы и преобразованы в диаграмму (см. рис. 5), позволяющую провести графическое сравнение измеренных и расчётных данных.

Из рис. 5 следует, что доверительные интервалы незначительно перекрыты, и для увеличения степени достоверности требуется больше испытаний с наработкой на отказ (особенно для варианта с прецизионно обработанными поверхностями). В любом случае данные показывают чёткую дифференциацию по ресурсу. На рисунке также отмечены расчётные ресурсы, полученные из уравнения (1) (звёздочки).

Расчётные ресурсы слегка завышены по сравнению с фактическими результатами измерений. Для зубчатых передач со шлифованными поверхностями такое завышение несколько больше, чем для зубчатых передач с прецизионно обработанными поверхностями. В данную модель можно внести уточняющие корректировки, проведя дополнительные испытания и ориентируясь на методы, уже использованные для подшипников качения. Однако на данном этапе главная цель состоит в том, чтобы дать первичную оценку основной теории без учёта уточняющих факторов. Основываясь на этом и принимая во внимание график на рис. 5, можно сделать вывод об очень высокой степени корреляции между результатами испытаний и расчётными данными, полученными с использованием представленной в данной работе методики.

Заключение

Концептуальная модель с разделением поверхностных и подповерхностных условий для учёта контактной усталости при качении, изначально разработанная для подшипников качения, теперь адаптирована и для зубчатых передач. В качестве примера проиллюстрировано влияние качества смазывания на усталостный ресурс.

Концептуальная модель может быть улучшена до прогнозной модели путём внесения уточняющих корректировок на основании большего количества данных, полученных в результате испытаний зубчатых передач при различных условиях эксплуатации. При этом особое внимание необходимо уделить влиянию таких факторов, как материал, качество смазывания, качество обработки поверхности и степень загрязнения твёрдыми частицами.

Однако даже в концептуальном виде модель уже может давать правильные результаты, коррелирующие с результатами испытаний прямозубых зубчатых передач, как следует из работ [12–15, 17]. В модели расчёта ресурса зубчатых передач впервые использован оценочный параметр для поверхности — динамическая грузоподъёмность поверхности.

Из представленного в данной работе анализа можно сделать следующие выводы:

1. Рассматриваемый подход позволяет разделить влияние поверхностных и подповерхностных условий на безотказную работу. Следовательно, это может дать значительный положительный эффект благодаря повышению гибкости моделирования для оценки ресурса зубчатых передач, поскольку такой анализ затрагивает более одной зоны. Это позволит инженерам учитывать поверхностные режимы отказа в дополнение к контактной усталости при качении по Герцу.
2. Поскольку в уравнении непосредственно учитывается влияние поверхностных эффектов, данный подход позволяет применять знания, полученные в результате использования современных трибологических моделей. В будущем в модель могут быть включены такие нетрибологические факторы, как напряжения в основаниях зубьев.
3. Использование для зубчатых передач понятий динамической грузоподъёмности поверхности и динамической грузоподъёмности подповерхностного слоя является инновацией, которая может обеспечить гибкий подход к расчёту ресурса зубчатых передач с особыми свойствами, непосредственно влияющими на рабочие характеристики поверхности (например, с термообработкой, покрытием или чистовой обработкой).
4. При проектировании редукторов чрезвычайно полезно было бы унифицировать методы расчёта ресурса зубчатых передач и подшипников качения не только в части схожих допущений, но и при оценке общей надёжности.