Effetti delle imperfezioni dei materiali
In SKF la ricerca per comprendere meglio gli effetti della microstruttura e delle imperfezioni preesistenti del materiale sulle prestazioni dei cuscinetti non si è mai fermata. Il lavoro presentato è fondamentale per definire quali caratteristiche e relative classi di gravità influiscono in maniera decisiva sulle prestazioni del cuscinetto.
Oggigiorno, i cedimenti dei cuscinetti dovuti a fatica da contatto di rotolamento (RCF, Rolling Contact Fatigue) in genere sono un evento raro e la durata di esercizio finale dei cuscinetti volventi di solito è superiore alla durata teorica calcolata. Tuttavia, vi sono casi in cui in applicazioni specifiche i cuscinetti si possono danneggiare prematuramente. Comprendere i meccanismi dei cedimenti dei cuscinetti è fondamentale per il miglioramento continuo delle loro prestazioni, in risposta all’esigenza di densità di potenza sempre maggiore posta dalle moderne applicazioni dei cuscinetti volventi.
L’affidabilità dei cuscinetti volventi utilizzati in varie applicazioni obbedisce al principio dell’elemento più debole, ovvero i cedimenti sono dovuti alla rottura dell’elemento più debole all’interno del sistema interessato. In condizioni di scarsa lubrificazione, i cedimenti dei cuscinetti possono essere dovuti a danneggiamenti superficiali come affaticamento o usura. Altrimenti l’elemento più debole si dovrebbe trovare nell’area sotto la superficie. Questo perché la sollecitazione di taglio derivante dal contatto hertziano raggiunge il limite massimo a una certa profondità sotto la superficie della pista. Inoltre, come la maggior parte dei materiali ad alta resistenza, l’acciaio per cuscinetti generalmente riduce la tolleranza ai danneggiamenti a causa di imperfezioni preesistenti nel materiale, quali le inclusioni non metalliche, che sono un sottoprodotto dei processi di fabbricazione dell’acciaio.
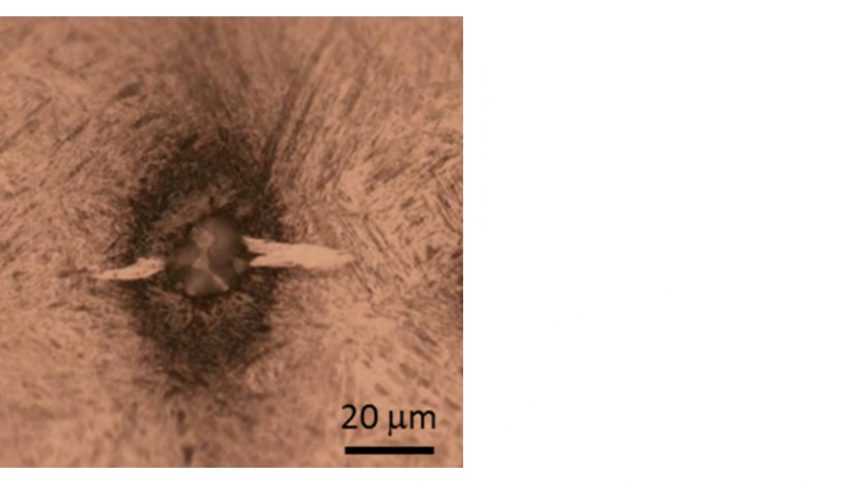
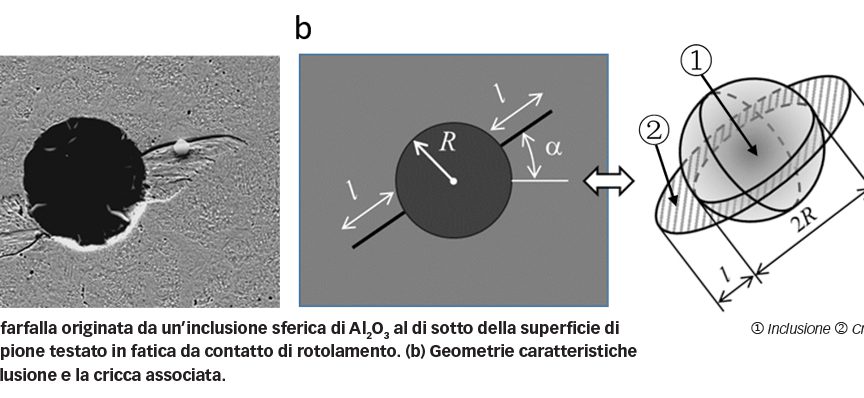
Indagini metallografiche condotte su campioni testati a fatica per contatto di rotolamento indicano che le cosiddette farfalle spesso si sviluppano da inclusioni non metalliche. La farfalla osservata in microscopia ottica da un campione sottoposto ad attacco Nital mostra due cricche derivanti da un’inclusione che presentano un’area di white etching, come illustrato in fig. 1. Tale area di white etching è la microstruttura alterata risultante dallo sfregamento tra le pareti delle cricche [1, 2]. In caso di carico da contatto di rotolamento, la cricca si potrebbe propagare fino a raggiungere la superficie della pista, con conseguente erosione superficiale.
Imperfezioni del materiale in fatica da contatto di rotolamento
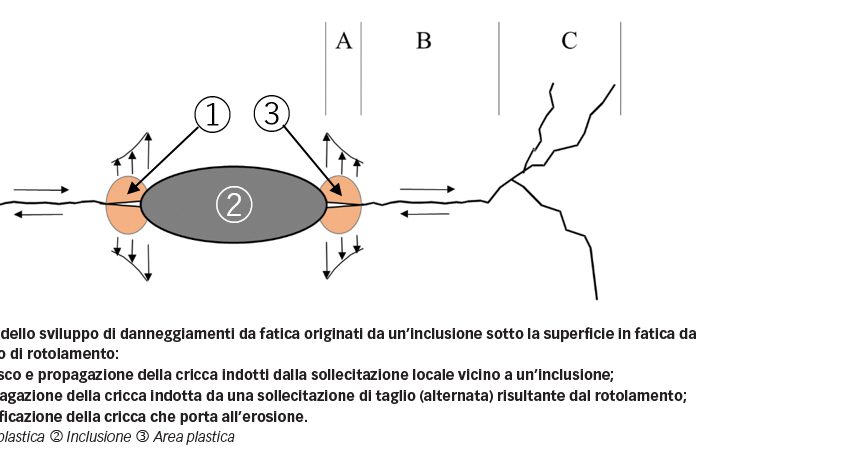
Il contatto di rotolamento sulle superfici della pista dei cuscinetti causa sollecitazioni cicliche che si estendono dalla superficie fino al di sotto di essa. A causa dell’effetto dell’aumento delle sollecitazioni, le cricche possono avere origine da inclusioni anche con una pressione di contatto inferiore al cosiddetto limite di shake down elastico, ovvero con una pressione di contatto al di sotto della quale il materiale nel suo complesso, ad eccezione delle aree vicine alle inclusioni, si comporta in modo elastico. Come illustrato in figura 2, il processo di danneggiamento si sviluppa in tre fasi, che alla fine possono portare all’erosione della superficie della pista dei cuscinetti.
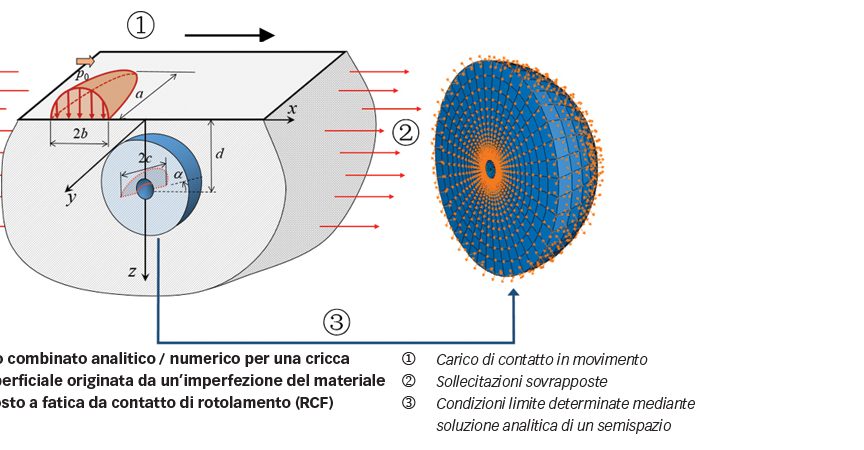
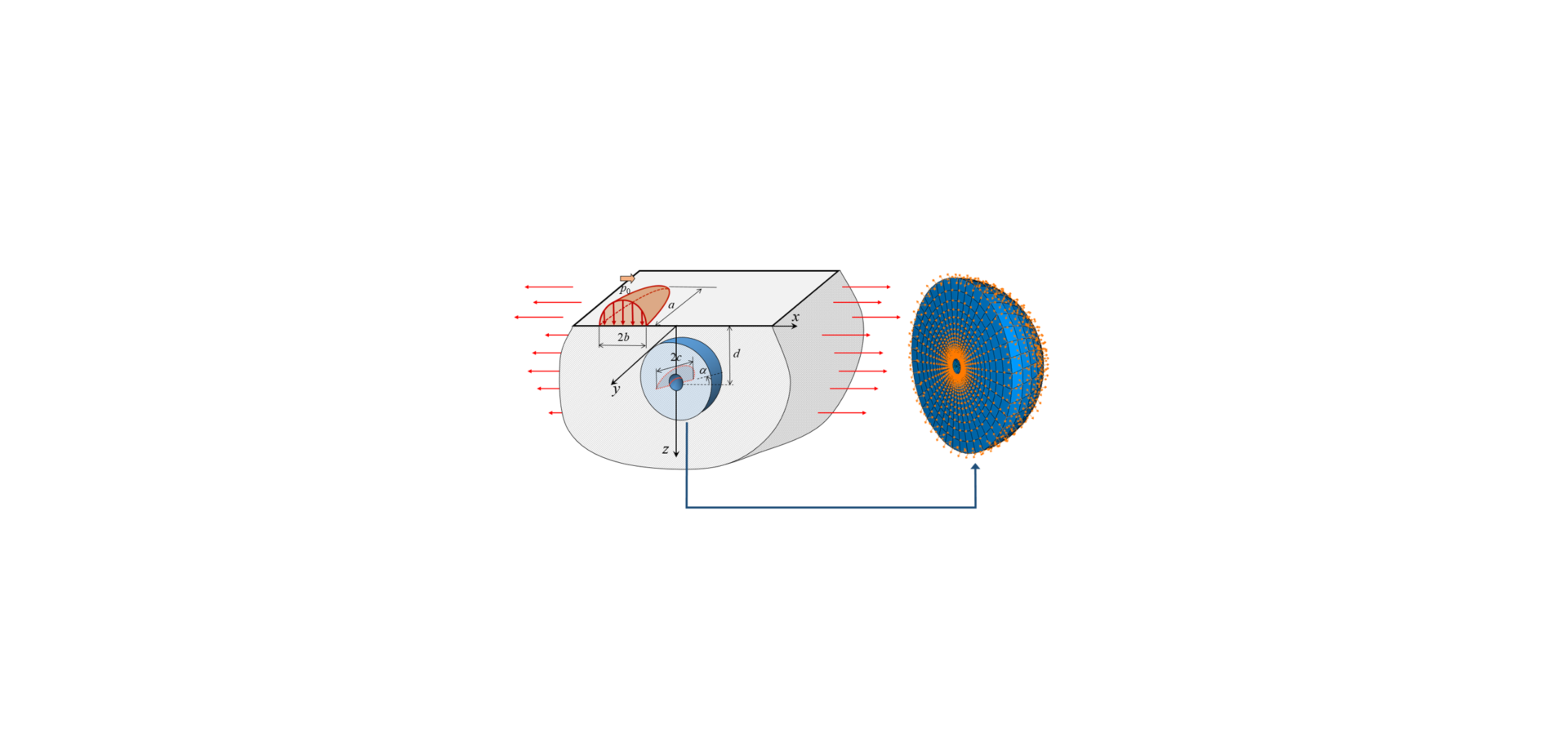
È stata sviluppata una nuova metodologia di modellazione che combina il metodo degli elementi finiti (FEM, Finite Element Method) con una soluzione analitica di un semispazio sottoposto a carico superficiale. Come illustrato in figura 3, uno strato di materiale intorno al difetto viene modellato con il metodo degli elementi finiti, mentre la deformazione e le sollecitazioni sotto la superficie derivanti da contatto di rotolamento vengono “trasmesse” dai nodi limite, nei quali gli spostamenti vengono prestabiliti utilizzando la soluzione analitica di un semispazio [3].
Sono stati considerati diversi tipi di inclusione, in termini di composizione o morfologia, e la condizione di aderenza tra le inclusioni e la matrice in acciaio. La simulazione a elementi finiti inoltre incorpora il comportamento elastoplastico dell’acciaio dei cuscinetti per tenere conto della plasticità localizzata.
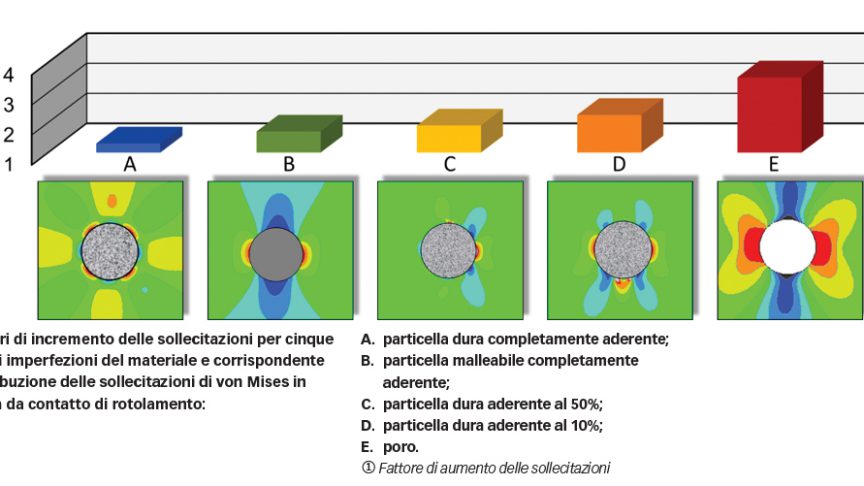
La figura 4 mostra i fattori di aumento delle sollecitazioni calcolati per numerose imperfezioni del materiale in fatica da contatto di rotolamento, inclusi particelle malleabili, dure e una porosità. Le particelle sono considerate solidi elastici con una rigidezza diversa da quella della matrice in acciaio. La figura 4 inoltre mostra la distribuzione delle sollecitazioni di von Mises vicino a ognuna delle inclusioni. L’inclusione completamente aderente ha un fattore di aumento delle sollecitazioni relativamente basso. Una particella malleabile completamente aderente ha un fattore di aumento delle sollecitazioni maggiore di quello di un’inclusione dura completamente aderente. Il fattore di aumento delle sollecitazioni aumenta in relazione al distacco tra l’inclusione e la matrice in acciaio. Una porosità è il caso estremo, perché ha il fattore di aumento delle sollecitazioni più alto.
La concentrazione delle sollecitazioni vicino a un’inclusione può causare plasticità locale dell’acciaio, che induce una sollecitazione di trazione residua localizzata. La sollecitazione di trazione residua, insieme ad altre componenti della sollecitazione locale vicino all’inclusione, potrebbe causare l’innesco della cricca e la propagazione iniziale della stessa, ovvero i danneggiamenti da fatica della fase A indicati in figura 2. I fattori di incremento delle sollecitazioni, mostrati in figura 4, indicano la pericolosità per inclusioni di diversa natura. Le particelle di nitruro di titanio, che in genere sono ben aderenti alla matrice in acciaio del cuscinetto, si sono rivelate molto meno pericolose delle inclusioni di ossido di alluminio, che sono sì particelle dure, ma presentano una scarsa aderenza alla matrice in acciaio, essendo addirittura distaccate da essa.
A fronte di una specifica pressione di contatto, l’innesco di una cricca da un’inclusione dipende innanzitutto dalle sollecitazioni locali vicine all’inclusione. In altre parole, l’innesco della cricca dipende dal tipo, ma non dalle dimensioni, dell’inclusione, perché il fattore di incremento delle sollecitazioni è indipendente dalle dimensioni dell’inclusione. Tuttavia, una cricca originata da un’inclusione non evolverà sempre in un’erosione. In alcuni casi la cricca si potrebbe arrestare in modo permanente.
L’evoluzione delle cricche da fatica viene analizzata nell’ambito della meccanica della frattura. La forza necessaria per la propagazione delle cricche da fatica può essere calcolata prendendo in considerazione le dimensioni della cricca e dell’inclusione (di un tipo specifico), le sollecitazioni sotto la superficie derivanti da contatto hertziano e le sollecitazioni sovrapposte, ad esempio sollecitazioni residue, sollecitazioni strutturali e/o circonferenziali, come indicato in figura 3. Se la forza necessaria supera un certo valore di soglia, la cricca si propaga e causa un cedimento. Altrimenti la cricca si arresta. Maggiore è la forza necessaria, tanto più rapidamente si propaga la cricca.
Si prenda in considerazione ad esempio un’inclusione sferica di raggio R, con una cricca anulare, di lunghezza l, come indicato in figura 5. La forza necessaria è proporzionale a , dove p0 √(R + l) è la pressione di contatto. Ciò significa che la forza necessaria aumenta con la pressione di contatto. Con un valore p0 specificato, la dimensione dell’inclusione, R, regola la velocità di evoluzione della cricca, in particolare durante la Fase-A in cui l è decisamente inferiore a R. L’influenza dell’inclusione diminuisce quando la cricca si propaga lontano dall’inclusione.
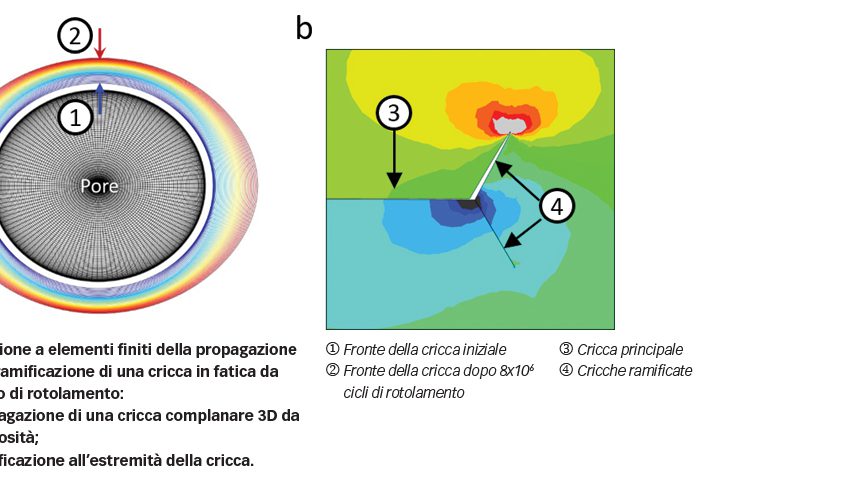
L’analisi a elementi finiti è stata condotta per simulare la propagazione di una cricca 3D da una porosità ellissoidale che rappresenta un’inclusione distaccata in fatica da contatto di rotolamento. La propagazione simulata della cricca, come mostrato in figura 6a, è stata confrontata con la configurazione della cricca osservata negli esperimenti a fatica da contatto di rotolamento. Si è riscontrata corrispondenza qualitativa tra il modello e l’esperimento.
La propagazione della cricca della fase B è indotta innanzitutto dalla sollecitazione di taglio alternata risultante da contatto di rotolamento, che prima o poi porta alla propagazione della cricca nella fase C, ovvero alla ramificazione della cricca dovuta a sollecitazioni di trazione e compressione alternate vicino all’estremità della cricca, come mostrato in figura 6b. C’è concorrenza tra l’evoluzione della cricca complanare in modalità di taglio e la ramificazione della cricca in modalità di trazione. La formazione della ramificazione della cricca può essere influenzata dalle sollecitazioni sovrapposte. Una sollecitazione di trazione favorisce la ramificazione della cricca e può ridurre la durata a fatica. Una sollecitazione di compressione è positiva, perché tende a evitare la ramificazione della cricca.
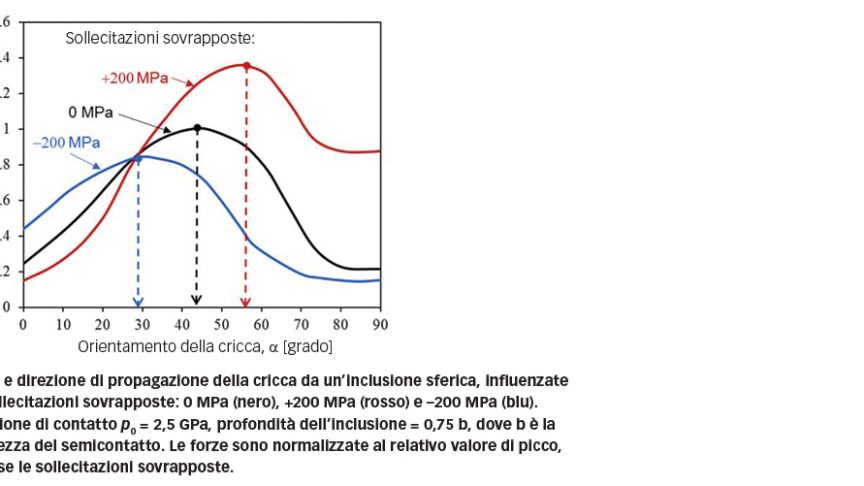
La figura 7 mostra la forza necessaria per la propagazione di una cricca originata da un’inclusione sferica come una funzione dell’orientamento della cricca, prendendo in considerazione una pressione di contatto di 2,5 GPa e livelli diversi di sollecitazioni sovrapposte. Sono state valutate le forze necessarie per cricche con diverso orientamento. In figura 7 si può osservare che, in assenza di sollecitazioni sovrapposte, la forza massima corrisponde a un orientamento della cricca di 45°. Se si applica una sollecitazione di compressione di 200 MPa, la curva della forza raggiunge il suo picco a un angolo di 30°; tuttavia, se si applica una sollecitazione di trazione di 200 MPa, l’orientamento della cricca a cui la forza raggiunge il limite massimo è aumentato a 57°. Si può affermare che una sollecitazione di trazione può accelerare la propagazione della cricca e tende a portare l’evoluzione della cricca verso un angolo retto, mentre una sollecitazione di compressione può ritardare l’evoluzione della cricca e tende a portare la propagazione della cricca in direzione orizzontale.
Significato dal punto di vista ingegneristico
La ricerca sui meccanismi di fatica ha portato all’identificazione di una delle cause principali dei cedimenti dei cuscinetti [2]. I cedimenti prematuri dei cuscinetti caratterizzati da cricche WEC (White Etching Crack) e cricche assiali sono stati riprodotti con successo in test di laboratorio, in cui l’anello interno di un cuscinetto a rulli cilindrici è stato montato sull’albero di una bussola con introduzione artificiale di difetti di planarità superficiale. È stato dimostrato, mediante simulazione a elementi finiti, che la deformazione della sede del cuscinetto può portare alla generazione di sollecitazioni di trazione vicino alla pista dell’anello interno, che, se superiori a un certo limite, possono ridurre la resistenza del materiale e, in combinazione con le sollecitazioni hertziane, comportare l’innesco prematuro e l’evoluzione accelerata delle cricche dalle imperfezioni preesistenti del materiale, con conseguenti cedimenti prematuri del cuscinetto.
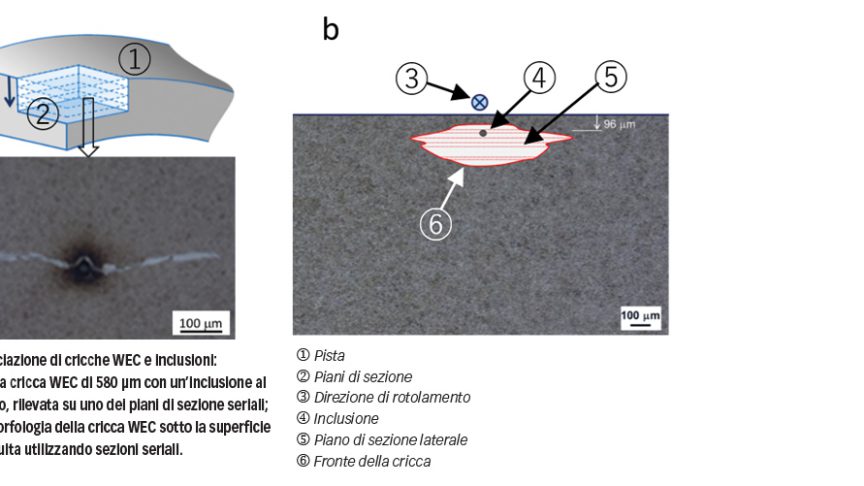
Inoltre, la verifica metallografica eseguita utilizzando sezioni seriali di spessore ridotto degli anelli testati ha indicato che le cricche WEC rilevate comunemente in cuscinetti con cedimenti prematuri possono essere originate da inclusioni sotto la superficie, come indicato in figura 8. A una conclusione analoga è giunta una ricerca indipendente riportata in [4]. Il significato di quanto scoperto offre un chiarimento sull’origine delle cricche WEC. Si può affermare che una cricca WEC è essenzialmente una cricca sotto la superficie, come una farfalla, che può aver avuto origine da un aumento delle sollecitazioni, ma è evoluta in uno stato avanzato. Lo sfregamento ripetuto tra le superfici della cricca in fatica da contatto di rotolamento causa l’alterazione graduale della microstruttura, che porta alla formazione delle aree di white etching (WEA) vicino alla superficie della cricca. Pertanto, la cricca WEC o l’area di white etching non è la causa dei cedimenti prematuri dei cuscinetti, ma un sintomo di danneggiamenti da fatica da contatto di rotolamento avanzati.
Sintesi
La ricerca sui meccanismi della fatica è fondamentale per l’avanzamento della tecnologia dei cuscinetti per affrontare le sfide poste dalle applicazioni più severe. Il lavoro presentato dimostra che una migliore comprensione delle imperfezioni del materiale e dei relativi effetti sulle prestazioni dei cuscinetti può fare nuova luce su alcuni problemi, per i quali è possibile trovare eventuali soluzioni per ridurre la frequenza dei cedimenti prematuri dei cuscinetti. Inoltre, possono essere determinati i limiti di tolleranza per le imperfezioni del materiale.
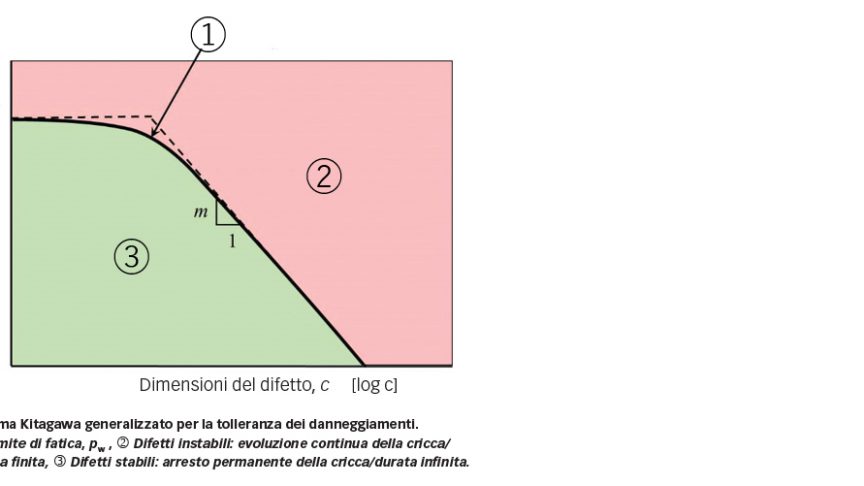
I limiti di tolleranza per le imperfezioni del materiale possono essere stabiliti in virtù di uno schema Kitagawa generalizzato che, come illustrato in figura 9, collega il limite di fatica, in termini di limite massimo della pressione di contatto, alle dimensioni del difetto. Quando il difetto diventa sempre più insignificante, la curva si avvicina al limite di fatica intrinseco del materiale della matrice. In caso di difetti di grandi dimensioni il limite di fatica può essere determinato dalla condizione di soglia per l’insorgere dell’evoluzione delle cricche da fatica, ovvero l’asintoto con una pendenza costante in –m, il cui valore dipende dal tipo di difetto.
Lo schema Kitagawa [6] originale è stato proposto per i difetti simili a cricche, dove m = 0,5. Lo schema Kitagawa generalizzato può essere applicato per diversi materiali e vari tipi di difetti. Ad esempio, è stato utilizzato per stabilire il limite di tolleranza per i difetti dovuti a materiale mancante sulla superficie delle sfere in nitruro di silicio per i cuscinetti ibridi [6]. Per questo tipo di difetto m è 0,46.
Sulla base della descrizione dell’innesco e della propagazione delle cricche da fatica originate da inclusioni sotto la superficie è stato sviluppato un modello per prevedere la resistenza a fatica con un numero molto elevato di cicli (VHCF, Very High Cycle Fatigue) e il limite di fatica dell’acciaio dei cuscinetti [7]. È stato dimostrato [8] che i limiti di fatica previsti e i dati dei test a fatica con un numero molto elevato di cicli sono correlati al valore del limite di fatica definito nella norma ISO 281:2007 per la durata utile dei cuscinetti volventi.
Bibliografia
[1] W. Solano-Alverez, H.K.D.H. Bhadeshia, White-etching matter in bearing steel. Part II: Distinguishing cause and effect in bearing steel failure, Metall. Mater. Trans. A 45A (2014) 4916-4931.
[2] J. Lai, K. Stadler, Investigation on the mechanisms of white etching crack (WEC) formation in rolling contact fatigue and identification of a root cause for bearing premature failure, Wear 364-365 (2016) 244-256.
[3] J.L. Johnson, Contact Mechanics, Cambridge University Press, 1985, Cambridge, UK.
[4] M. Evans, White structure flaking failure in bearings under rolling contact fatigue, PhD Thesis, University of Southampton, UK, 2013.
[5] H. Kitagawa, S. Takahashi, Applicability of fracture mechanics to small cracks or cracks in the early stage. In: Proceedings of the second international conference on mechanical behaviour of materials. ASM, 1976, pp. 627-631.
[6] J. Lai, Y. Kadin, C. Vieillard, Characterization and modelling of the degradation of silicon nitride balls with surface missing-material defects under lubricated rolling contact conditions, Wear 398-399 (2018) 146-157.
[7] J. Lai, T. Lund, K. Ryden, A. Gabelli, I. Strandell, The fatigue limit of bearing steels – Part I: A pragmatic approach to predict very high cycle fatigue strength, Int. J. Fatigue 38 (2012) 155-168.
[8] A. Gabelli, J. Lai, T. Lund, K. Rydén, I. Strandell, G.E. Morales-Espejel, The fatigue limit of bearing steels – Part II: Characterization for life rating standards, Int. J. Fatigue 38 (2012) 169-180.