Der Wunsch nach zuverlässigeren, trotzdem aber kompakteren und preiswerteren Produkten macht eine exaktere Bestimmung der Lebensdauer von Wälzlagern erforderlich. Dies hat Forscher veranlasst, die Berechnung der Lagerlebensdauer unter Einbeziehung neuester technischer Erkenntnisse weiterzuentwickelnDie Lebensdauerberechnung von Wälzlagern basiert auf Arbeiten von Gustaf Lundberg und Arvid Palmgren aus dem Jahr 1947. Die Lebensdauergleichung ist anhand der Weibull’schen Wahrscheinlichkeitsverteilung von 1936 erstellt. Dadurch konnte in die Berechnung die Lagerzuverlässigkeit einbezogen werden. Dies stellte einen wesentlichen Fortschritt bei den Bemühungen dar, die Lebensdauer eines so wichtigen Maschinenteils rechnerisch im Voraus bestimmen zu können.
Die Möglichkeit, die Lebensdauer eines Lagers vorauszubestimmen und, anhand rationaler Kriterien, ein Lager für einen bestimmten Anwendungsfall auszuwählen, war ein technischer Durchbruch. Seitdem haben Wissenschaft und Technik, insbesondere auf dem Gebiet der Tribologie, erhebliche Fortschritte gemacht. Die neuesten theoretischen Erkenntnisse und Berechnungsverfahren finden mit Hilfe leistungsstarker Computer ihren Niederschlag in weiterentwickelten Techniken und Lagerkonstruktionen. Zusätzlich können heute sauberere Stähle mit gleichmäßiger Legierung und besserer Qualität hergestellt werden. Bessere Schmierstoffe sorgen für zuverlässigere Trennung der metallischen Berührungsflächen im Wälzkontakt. Mit modernen Fertigungsmethoden können genauere Lager mit immer höherer Qualität gefertigt werden.
Derartige technologische Fortschritte erfordern Berechnungsmethoden, die die höhere Leistungsfähigkeit moderner Wälzlager wirklich berücksichtigen. Bis vor kurzem wurden die Leistungsverbesserungen im wesentlichen durch Anhebung der dynamischen Tragzahlen nutzbar gemacht, was rechnerisch eine längere Lebensdauer zur Folge hat. Auch wurden Beiwerte für die Lebensdauerwahrscheinlichkeit und Betriebsbedingungen in die Berechnung mit einbezogen. Diese Art der Lebensdauerberechnung wurde lange Zeit für ausreichend angesehen.
Untersuchungen über die wesentlichen Ausfallursachen in modernen Wälzlagern haben neue Erkenntnisse gebracht. So gehen Ermüdungsausfälle häufiger von der Laufbahnoberfläche aus als von Rissen unterhalb der Oberfläche. Entsprechend sind Oberflächengüte und Verunreinigung der Lager stärker in den Mittelpunkt getreten. Auch wurde für moderne Wälzlagerstähle eine Ermüdungsgrenzbelastung festgestellt. Aufgrund solcher Überlegungen wurden verbesserte Lebensdauergleichungen erarbeitet und Untersuchungen über den Einfluss von Verunreinigungen und Oberflächenbehandlung auf die Lagerleistung angestellt.

Das Modell der Ermüdungslebensdauer im Wälzkontakt von Eustathios Ioannides und Tedric Harris (1985), erweitert die Wälzermüdungstheorie von Lundberg und Palmgren in zwei wesentlichen Punkten

i) Es wird eine Ermüdungsgrenzspannung eingeführt, unterhalb derer mit keiner Ermüdung im Lager zu rechnen ist.

ii) Das beanspruchte Volumen im Kontaktbereich wird als Menge relative kleiner Volumenelemente definiert, die jeweils individuellen lokalen Spannungen ausgesetzt sind.

So lassen sich echte lokale Spannungen sowie die Auswirkungen von Spannungskonzentrationen an der Oberfläche, etwa Kantenspannungen und Eindrückungen überrollter Teilchen, in die Lebensdauerberechnungen einfügen. Ein solcher umfassender Ansatz zur Berechnung der Lagerlebensdauer macht komplexe Computerprogramme erforderlich, weil das Ausfallrisiko für komplizierte Spannungsfelder berechnet werden muss. Da viele Lageranwender keinen Zugriff auf solche Rechenprogramme haben, müssen sie mit den in den Wälzlagerkatalogen oder Normen angegebenen Gleichungen rechnen.
Um den Nutzen aus unserer technologischen Fortentwicklung und den neuen Erkenntnissen allen zur Verfügung stellen zu können, haben wir die SKF Lebensgleichnung erarbeitet. Der Durchschnittswert der tatsächlichen gewichteten Spannung über dem Werkstoffvolumen mit Ausfallrisiko ist hier einbezogen. Die von Lundberg und Palmgren entwickelten Gleichungen wurden um die Ermüdungsgrenzbelastung und die wirksamen Ermüdungskriterien für ein Volumenelement im Lager ergänzt. Zur praktischen Umsetzung wird dazu ein Beiwert für die Spannung eingeführt, der die Ermüdungsgrenzbelastung des Lagers beeinflusst. Dieser Faktor berücksichtigt den tatsächlichen Spannungszustand, der von der Hertz’schen Spannungsverteilung abweicht. Dadurch ergab sich eine einfache Gleichung, die der in ISO 281:1990 genormten Gleichung sehr ähnlich ist. Diese Lebensdauergleichung ist genau so einfach aufgebaut wie die bisherige Tragfähigkeit/Belastungs-Gleichung, kann jedoch die Leistungsfähigkeit moderner Lager genauer erfassen.

Herleitung der Gleichungen
Grundlage für die Voraussage der Ermüdungslebensdauer von Wälzlagern sind unterschiedliche Modelle. Das herkömmliche Modell geht davon aus, dass die Wahrscheinlichkeit, mit der ein Volumenelement eine Anzahl von Spannungsspitzen erlebt, bis ein Ermüdungsriss unter der Oberfläche zur Oberfläche durchtritt, seiner Größe proportional und eine Funktion seines Ortes und der Anzahl der bereits ertragenen Spannungszyklen ist. Lundberg und Palmgren verwendeten 1947 die Weibull’sche Wahrscheinlichkeitsverteilung der metallischen Ermüdung von 1939, um die grundlegende Theorie zur stochastischen Verteilung der Lagerlebensdauer laut untenstehender Gleichung zu entwickeln:

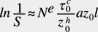        (1)

Unter Zugrundelegung der Hertz’schen Spannungsverteilung in Abhängigkeit von der aufgebrachten Last und der Geometrie des Berührungsfläche leiteten sie eine Beziehung zwischen der Belastung und der Lagerlebensdauer ab, die sich in folgende einfachen Form bringen ließ:

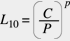        (2)

L ist die erwartete Lebensdauer in Millionen Umdrehungen bei der Belastung P. C ist die dynamische Tragzahl, die von der Lagergeometrie abhängt. Der Exponent p beträgt 3 für Kugellager und 10/3 für Rollenlager. Gleichung 2 wurde letztendlich 1962 in die ISO Empfehlung ISO/R281 aufgenommen. 1977 wurden mit der modifizierten Lebensdauergleichung die Beiwerte a₁, a₂ och a₃ eingeführt, die die Erlebenswahrscheinlichkeit, die Werkstoffeigenschaften und die Schmierung berücksichtigen. Daraus entstand die heute noch gültige und in ISO 281:1990 genormte Lebensdauergleichung:

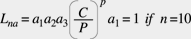        (3)

In Kenntnis der Wechselwirkung von Werkstoff und Schmierung empfehlen viele Wälzlagerhersteller auch die Anwendung der folgenden Gleichung:

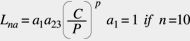        (4)

Die SKF Lebensdauergleichung
Eine einfache analytische Gleichung der Lagerlebensdauer, die auch die Ermüdungsfestigkeit des Werkstoffs berücksichtigt, wurde aus dem Ermüdungsmodell von Ioannides und Harris (1985) abgeleitet. Sie war ursprünglich zur Berechnung des Ausfallrisikos in dreidimensionalen Spannungsfeldern eingesetzt worden. Da die Beanspruchung aus der Berührung zweier Körper nach der Hertz’schen Formel modellunabhängig ist, können bei Vorliegen reiner Hertz’scher Pressung Vereinfachungen vorgenommen werden. Dies ist möglich durch die Einführung von Spannungskriterien auf der Basis einer maximalen Orthogonal-Schubspannung t₀ oberhalb eines Schwellenwerts und einer Ermüdungsgrenzspannung t_u im Wälzkontakt . In Gleichung 1 kann dann die maximale Orthogonal-Schubspannung t₀ der Hertz’schen Pressung durch den Ausdruck t₀ – t_u ersetzt werden:

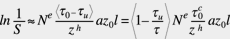        (5)

Der in dieser Gleichung in spitze Klammern gesetzte Term wird, wenn der Betrag negativ wird, auf Null gesetzt. Die Lebensdauergleichung für Wälzlager beim Vorliegen einer Ermüdungsgrenzbelastung erhält man mit Gleichung 5. Diese Gleichung unterscheidet sich von der ursprünglichen Gleichung von Lundberg und Palmgren (Gleichung 1) nur durch den in spitze Klammern gesetzten Term. Daher kann eine Gleichung für die Lagerlebensdauer entsprechend der von Lundberg und Palmgren aufgestellt werden. Unter Einbeziehung der äquivalenten Lagerbelastung und der dynamischen Tragzahl ergibt sich bei einer Ausfallwahrscheinlichkeit von 10 % die Lagerlebensdauer aus:

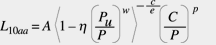        (6)

Hierin ist der Parameter h ein spannungsabhängiger Beiwert zur Lebensdauerbestimmung, der die tatsächlichen Spannungen im realen Wälzkontakt berücksichtigt. Dieser Parameter wird bei der Berechnung der Hertz’schen Pressung, von der Lundberg und Palmgren 1947 die ursprüngliche Formel abgeleitet haben, nicht berücksichtigt. Es hat sich gezeigt, dass der Parameter h außer von Maßänderungen, wie sie bei der Wärmebehandlung oder der Montage auftreten können, im wesentlichen vom Schmierzustand des Wälzkontakts und von Spannungskonzentrationen im Mikrobereich aufgrund von Eindrückungen oder Unebenheiten abhängt. Entsprechend wird der Parameter h als Funktion von den Umgebungsbedingungen (Schmierung und Verunreinigung) und der Lagergröße angegeben.

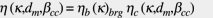        (7)

Durch Einsetzen von Gleichung 7 in Gleichung 6 erhält man:

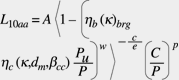        (8)

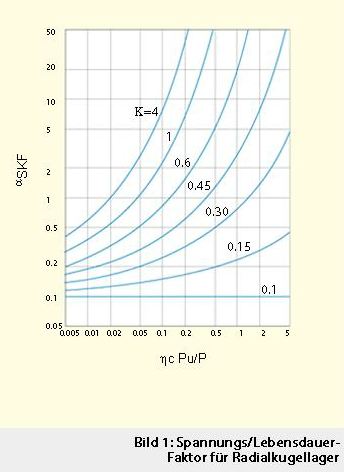
Zur Vereinfachung dieser Formel hat SKF 1989 den Beiwert a_SKF für die folgenden Lagerbauarten eingeführt: Radialkugellager, Radialrollenlager, Axialkugellager und Axialrollenlager. Dieser Beiwert kann für Radialkugellager aus dem in Bild 1 gezeigten Diagramm ermittelt werden und errechnet sich wie folgt:

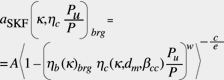         (9)

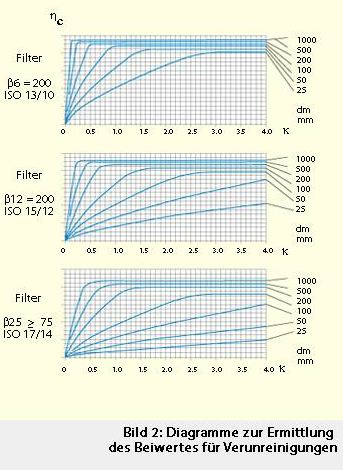
Des weiteren wurden Diagramme zur Ermittlung von h_c in Abhängigkeit von k, d_m, b_cc erstellt, wie von Bergling und Ioannides in 1994 sowie von Ioannides und Kollegen in 1999 vorgestellt. Bild 2 zeigt einige dieser h_c -Kurven. Unter Anwendung dieser Kurven lässt sich die Lebensdauergleichung 8 wie folgt vereinfachen:

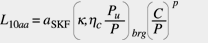        (10)

Die Lebensdauergleichung wird im SKF Hauptkatalog seit 1989 in dieser Form verwendet. Mit dieser Gleichung und den Diagrammen entsprechend Bild 1 und 2 kann die Lebensdauer von Wälzlagern genauso einfach berechnen werden wie bisher nach ISO 281:1990. Mit der Gleichung 10 können jetzt aber auch Schmierung und Verunreinigungen berücksichtigt werden. Das ergibt bei leichter Lagerbelastung, sauberen Betriebsbedingungen und guter Schmierung eine wesentlich längere Lebensdauer.

Experimentelle Bestätigung
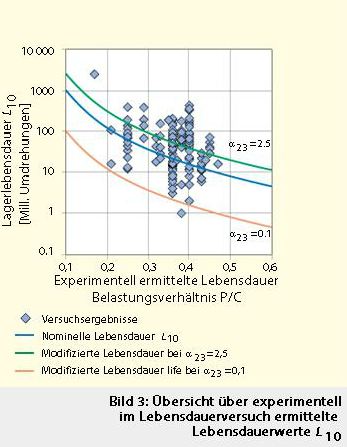
Die Richtigkeit der SKF Lebensdauergleichung (10) wurde in umfassenden Lebensdauerversuchen an über 8 000 Lagern bei unterschiedlichen Schmierungs- und Verunreinigungszuständen nachgewiesen. Einen Überblick über die in Lebensdauerversuchen ermittelten Lebensdauerwerte L₁₀ gibt Bild 3. Die vorher errechnete Lebensdauer und die tatsächlich erreichte Lebensdauer sind gegenübergestellt. Dazu wurde das Verhältnis zwischen der in Versuchen ermittelten Lebensdauer und der rechnerischen Lebensdauer der Lager, also a_exp=L_10exp/L₁₀ über dem betreffenden Parameter h_c P_u/P aufgetragen.
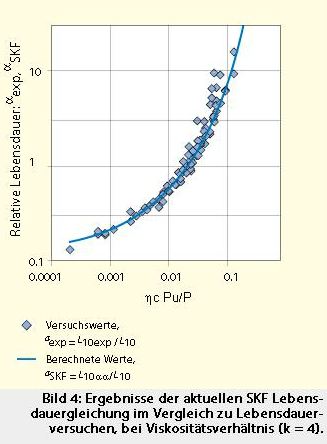
Bild 4 zeigt die Versuchsergebnisse mit ölgeschmierten Kugellagern bei einem Viskositätsverhältnis k = 4. Diese liegen im wesentlichen auf der für diese Verhältnisse nach der Gleichung 9 für a_SKF errechneten Wert. Bild 4 zeigt eine gute Übereinstimmung zwischen der relativen Lebensdauer nach der SKF Lebensdauergleichung und den bei den Lebensdauerversuchen erzielten Werten. Die umfassende Bewertung aller Versuchsergebnisse zeigte, dass die SKF Lebensdauergleichung eine bessere Übereinstimmung zwischen der Theorie und Praxis liefert, als die bisherige Lebensdauergleichung. Auch gibt die asymptotische Abnahme des Wertes für den Spannungs/ Lebensdauer-Faktor askf in Abhängigkeit von den Parametern k und h_c P_u/P einen weiteren Hinweis auf die angenommene Ermüdungsgrenzbelastung im Wälzkontakt, Bilder 1 und 4. Der Kurvenverlauf für das Spannungs/Lebensdauer-Verhältnis in Bild 4 ähnelt dem der bekannten Wöhler-Kurven, die die Überlebenswahrscheinlichkeit von Prüfstücken bei unterschiedlicher Spannung im Belastungstest angeben.

Schlussfolgerungen
Wälzlager können bei minimaler Reibung zuverlässig hohe Belastungen bei hohen Drehzahlen aufnehmen. Nur diese Technik ermöglichte die Mechanisierung unserer Umwelt, die das letzte Jahrhundert beherrschte und unser Leben verändert hat. Praxisbezogene Möglichkeiten, Wälzlager mit größerer Sicherheit auswählen und betreiben zu können, haben entscheidende Auswirkungen auf Betrieb, Wirtschaftlichkeit und Kosten von Maschinen. Und das betrifft uns alle, über den Energieverbrauch bis hin zu den allgemeinen Infrastrukturkosten. Mit der SKF Lebensdauergleichung steht eine genauere Methode zu Vorhersage der Lagerlebensdauer zu Verfügung. Sie erfüllt so die Forderungen nach ständigen Verbesserungen bei der Ausführung, der Auswahl und der Anwendung von Lagern.
Die SKF Lebensdauergleichung beschreibt das komplexe tribologische System, in dem ein Lager läuft, mit Hilfe weniger Parameter. Das Modell beschränkt sich auf wenige Größen, die einen wesentlichen Einfluss auf die Lebensdauer haben. Die SKF Lebensdauergleichung macht darüber hinaus deutlich, dass die von den einzelnen Parametern herrührenden Ermüdungsanteile nicht als lineare Überlagerung die Lagerlebensdauer beeinflussen. Besser als die einzelnen Beiwerte für Schmierung oder Verunreinigung kann ein einziger, der vieldimensionale Beiwert a_SKF als Funktion von k und h_c P_u/P den tribologischen und physikalischen Zustand des Systems beschreiben. Dieser Ansatz bietet die vorteilhafte Nutzung der vorgegebenen Daten durch den Konstrukteur und den Betreiber einer Maschine. Die gute Übereinstimmung mit den Versuchsergebnissen und die höhere Genauigkeit der SKF Lebensdauergleichung sprechen für dieses Verfahren zur Ermittlung der Lebenserwartung heutiger Wälzlager.

E. Ioannides, G. Bergling and A. Gabelli „An Analytical Formulation for the Life of Rolling Bearings“. Acta Polytechnica Scandinavica, MES No. 137, Espoo 1999.

Eustathios Ioannides, SKF Engineering and Research Centre (ERC), Nieuwegein,
Niederlande, und Imperial College of Science, Technology and Medicine, London, UK;
Gunnar Bergling, AB SKF, Göteborg, Schweden, und
Antonio Gabelli, SKF Engineering and Research Centre (ERC), Nieuwegein, Niederlande.