Einfluss von Materialfehlern
Um den Wissensstand hinsichtich der Auswirkungen von Gefügeunregelmäßigkeiten und Materialfehlern auf die Lagerleistung zu erweitern, wird bei SKF kontinuierlich Forschung betrieben. Die vorliegende Arbeit ist grundlegend für die Bestimmung der Lagerleistung als Funktion verschiedener Materialfehler und deren Schweregraden.
Lagerausfälle infolge von Wälzkontaktermüdung (RCF) sind heutzutage in der Regel selten, und die letztendlich erreichte Laufzeit von Wälzlagern liegt üblicherweise über der berechneten Lebensdauer. Es gibt jedoch Fälle, in denen Lager in bestimmten Anwendungen vorzeitig ausfallen können. Um den steigenden Anforderungen an die Leistungsdichte bei modernen Wälzlageranwendungen gerecht zu werden, ist die Kenntnis der Lagerausfallmechanismen für eine kontinuierliche Verbesserung der Lagerleistung von grundlegender Bedeutung.
Die Zuverlässigkeit von Wälzlagern, die in den verschiedensten Anwendungen eingesetzt werden, folgt dem Prinzip des schwächsten Glieds. Schwachstellen gibt es immer im Werkstoff oder auf der Wälzkontaktfläche. Ein Lager versagt, wenn das schwächste Glied der Kette gebrochen ist. Bei schlechter Schmierung oder rauer Oberfläche (z. B. nach Partikeleindrückungen) könnte das schwächste Glied an der Oberfläche liegen, und das Lager fällt aufgrund von Oberflächenschäden wie Oberflächenzerrüttung oder Verschleiß aus. Bei guten Schmierbedingungen könnte das schwächste Glied unter der Oberfläche liegen, da Materialfehler wie Einschlüsse und hohe Schubspannungen durch Hertz’sche Pressung vorliegen und der Lagerausfall auf eine Rissbildung und -ausbreitung aufgrund bereits vorhandener Materialfehler zurückzuführen ist. Darüber hinaus weisen hochfeste Werkstoffe eine eingeschränkte Schädigungstoleranz bzw. eine Anfälligkeit für bereits vorhandene Materialfehler wie nichtmetallische Einschlüsse als Nebenprodukt der Stahlherstellung auf.
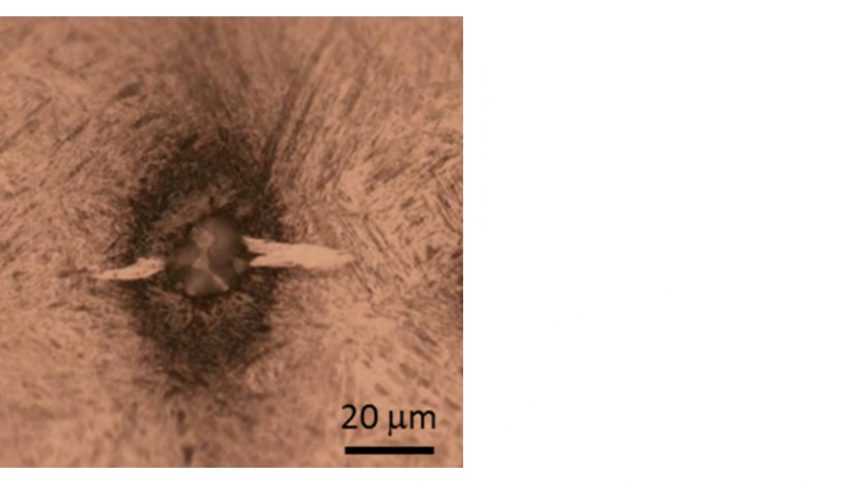
Metallografische Untersuchungen an RCF-Proben zeigen, dass sogenannte „Butterflies“ meist im Bereich von nichtmetallischen Einschlüssen entstehen. Bild 1, eine mit Nital geätzte Probe unter einem Lichtmikroskop, zeigt weiß dekorierte Risse symmetrisch von einem Einschluss ausgehend; daher der Name „Butterfly“. Die weiß anätzende Zone ist ein durch Rissflankenreibung [1, 2] verändertes Gefüge. Je nach Belastung des Wälzkontakts kann sich solch ein Riss ausbreiten und schließlich bis zur Laufbahnoberfläche durchbrechen, gefolgt von großflächigen Ausbrüchen bzw. Schälungen an der Oberfläche.
Materialfehler bei Wälzkontaktermüdung
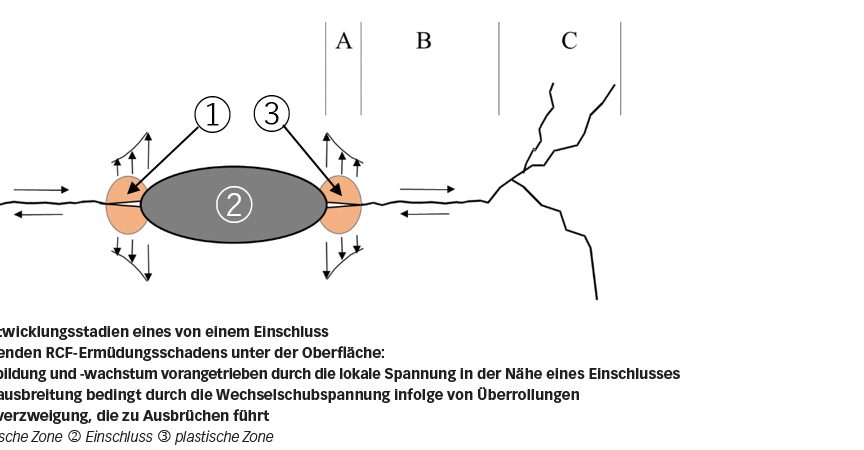
Der Wälzkontakt auf den Lagerlaufbahnen führt zu zyklischen Spannungen von der Oberfläche bis in die Tiefe des Lagermaterials. Aufgrund der spannungserhöhenden Wirkung können Risse ausgehend von Einschlüssen auch bei einem Kontaktdruck unterhalb der sogenannten elastischen „Shakedown“-Grenze entstehen, das heißt, einem Kontaktdruck unterhalb dem sich das Gesamtmaterial, mit Ausnahme der Bereiche um die Einschlüsse herum, elastisch verhält. Wie in Bild 2 dargestellt, besteht der Schadensprozess aus drei Stadien, die schließlich zu Ausbrüchen an den Oberflächen der Lagerlaufbahnen führen können.
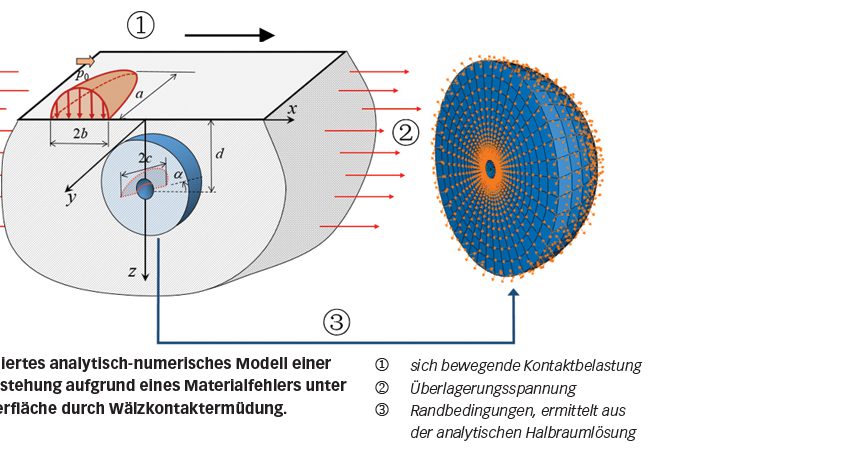
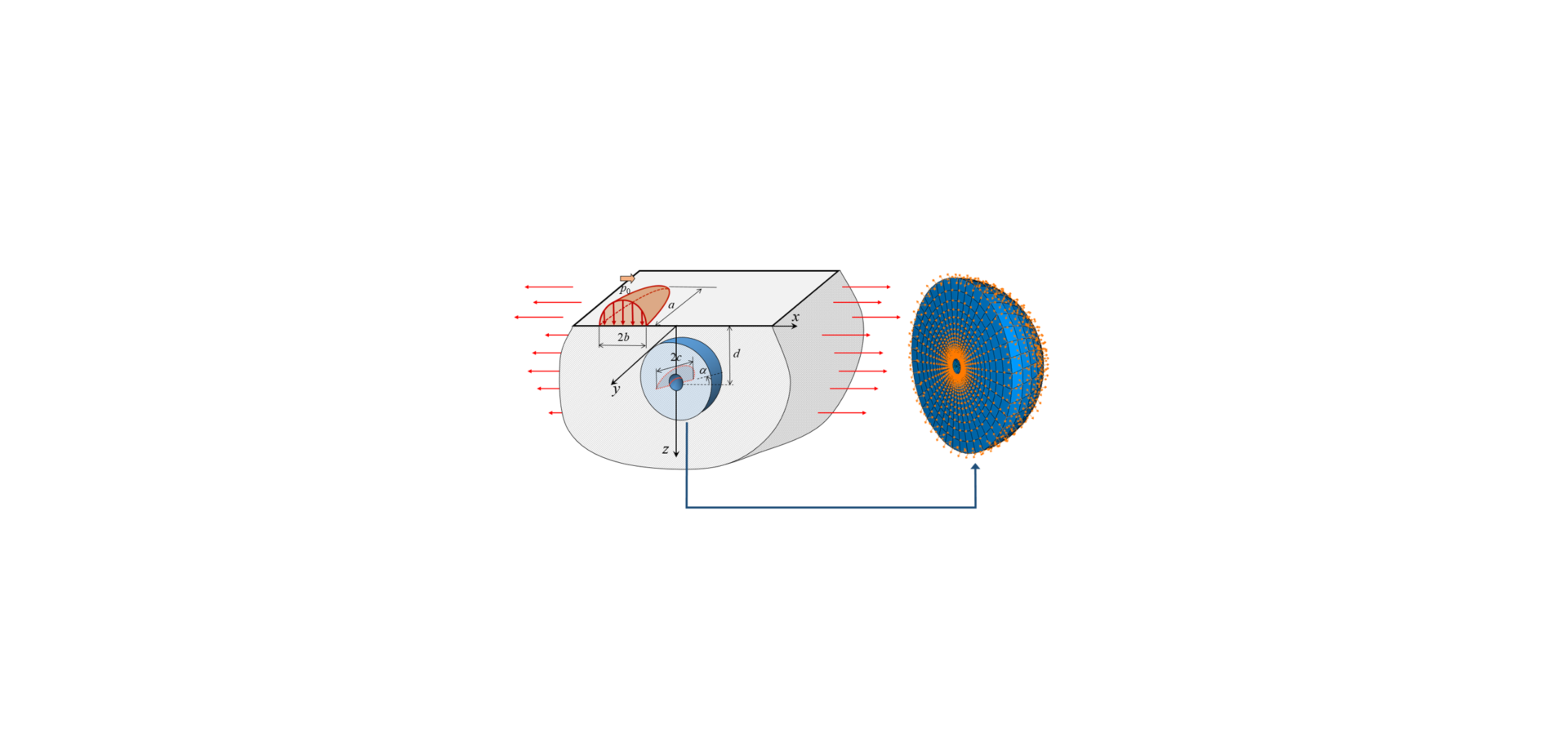
Eine neue Modellierungsmethode wurde entwickelt, welche FEM mit der analytischen Lösung eines Halbraums während einer Wälzlagerlaufbahnbelastung kombiniert. Wie in Bild 3 dargestellt, wird mit Hilfe der FEM eine Materialschicht um einen Materialfehler modelliert, während die analytische Halbraumlösung die Beanspruchung des Bereichs unter der Laufbahnoberfläche und die durch den Wälzkontakt hervorgerufene Verformung und Verschiebungen an die Randknoten „überträgt“ [3].
Verschiedene Einschlüsse bezüglich Zusammensetzung, Morphologie als auch Art der Einbindung in die Stahlmatrix werden berücksichtigt. Die FE-Simulation beinhaltet auch das elastisch-plastische Verhalten von Lagerstählen aufgrund der lokalen Plastizität.
Bild 4 zeigt die berechneten Spannungserhöhungsfaktoren mehrerer Materialfehler bei Wälzkontaktermüdung für weiche Einschlüsse, harte Einschlüsse und Porositäten. Die Einschlüsse werden als elastische Feststoffe betrachtet, deren Steifigkeit sich von der der Stahlmatrix unterscheidet. Bild 4 zeigt auch die von Mises-Spannungsverteilung im Bereich der Einschlüsse. Ein vollständig eingebundener harter Einschluss führt zu einer relativ geringen Spannungserhöhung. Zum Vergleich, ein vollständig eingebundenes weiches Teilchen dagegen führt zu einer höheren Spannung. Der Spannungserhöhungsfaktor nimmt mit dem Grad der Ablösung zwischen Einschluss und Stahlmatrix zu. Der Extremfall ist eine Pore mit dem höchsten Spannungserhöhungsfaktor.
Die Spannungskonzentration in der Nähe eines Einschlusses kann zu einer lokalen Plastizität des Stahls führen, die wiederum eine lokale Zugeigenspannung induziert. Letztere kann im Bereich des Einschlusses zu einer Rissbildung und anfänglichen Rissausbreitung führen, das heißt, Stadium A wie in Bild 2 dargestellt. Der Grad der Spannungserhöhung in Bild 4 weist auf die Schädlichkeit verschiedener Einschlüsse hin. Titannitridpartikel, die normalerweise gut in die Lagerstahlmatrix eingebunden sind, haben sich als wesentlich weniger schädlich erwiesen als Aluminiumoxideinschlüsse, die ebenfalls harte Partikel sind, aber eine schlechtere Einbindung in die Stahlmatrix haben und oft von ihr losgelöst sind.
Bei einem bestimmten Kontaktdruck ist die Rissbildung ausgehend von einem Einschluss in erster Linie von der lokalen Spannung im Bereich des Einschlusses abhängig. Das heißt, die Rissbildung richtet sich nach der Art, nicht aber nach der Größe des Einschlusses, da der Spannungserhöhungsfaktor unabhängig von der Einschlussgröße ist. Allerdings entwickeln sich aus einem Riss, der von einem Einschluss ausgeht, nicht immer Ausbrüche. Unter bestimmten Umständen kann der Riss dauerhaft gestoppt werden.
Das Ermüdungsrisswachstum wird im Rahmen der Bruchmechanik analysiert. Wie in Bild 3 dargestellt, kann die Triebkraft für das Wachstum von Ermüdungsrissen berechnet werden unter Berücksichtigung der Größe des Risses, der Art des Einschlusses, aus dem Hertz‘schen Kontakt und der Überlagerungsspannungen wie Eigenspannungen, Struktur- und/oder Ringspannungen unter der Oberfläche. Überschreitet die Triebkraft einen bestimmten Schwellenwert, breitet sich der Riss aus und führt zu einem Ausfall. Im anderen Fall wird der Riss gestoppt. Je stärker die Triebkraft, desto schneller breitet sich ein Riss aus.
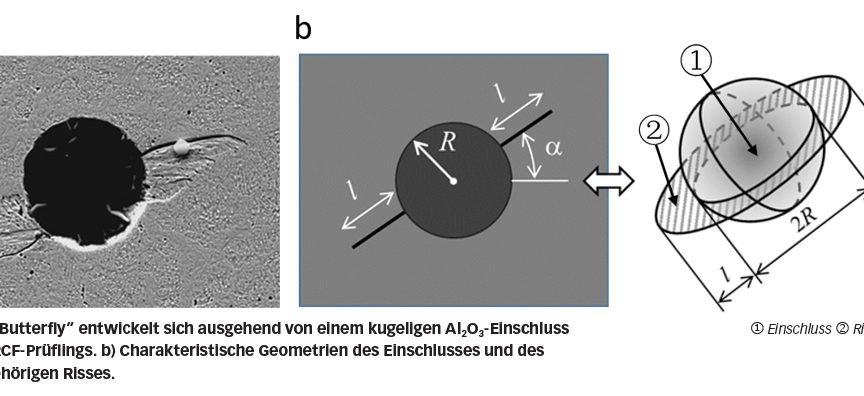
Man betrachte beispielsweise einen kugeligen Einschluss mit dem Radius R und einem ringförmigen Riss der Länge l (siehe Bild 5). Die Triebkraft ist proportional zu p0 √(R+l), wobei p0 der Kontaktdruck ist. Das bedeutet, dass die Triebkraft mit dem Kontaktdruck zunimmt. Bei einem spezifizierten Kontaktdruck p0 bestimmt die Größe des Einschlusses R die Geschwindigkeit des Risswachstums, insbesondere im Stadium A, in dem l viel kleiner ist als R. Der Einfluss des Einschlusses nimmt ab, wenn sich der Riss vom Einschluss weg ausbreitet.
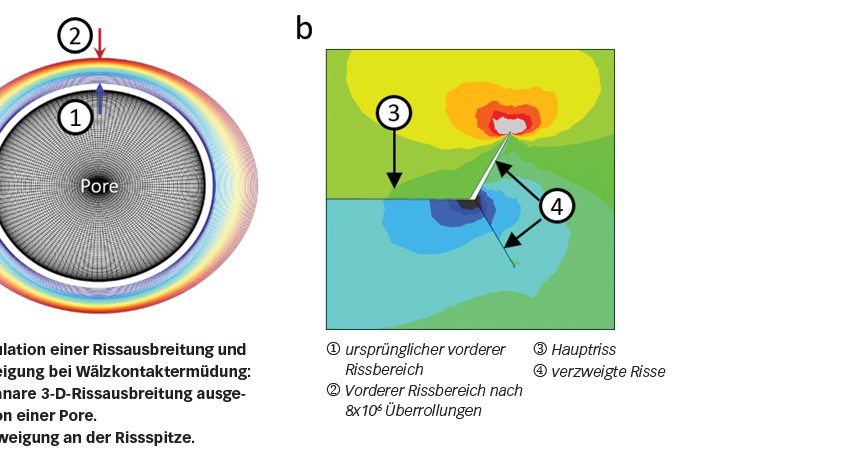
FEM-Analysen zur Simulation eines 3-D-Risses ausgehend von einer ellipsoiden Pore, die einen von der Stahlmatrix abgelösten Einschluss darstellt, wurden durchgeführt. Die simulierte Rissausbreitung, wie in Bild 6a dargestellt, wurde mit der Riss-Konfiguration aus RCF-Versuchen verglichen. Dabei wurde eine gute qualitative Übereinstimmung zwischen der Simulation und dem Versuch festgestellt.
Die Rissausbreitung Stadium B (siehe Bild 2) erfolgt in erster Linie durch die aus dem Wälzkontakt resultierende Wechselschubspannung, die früher oder später zu einer Rissverzweigung nach Stadium C führt. Das heißt, aufgrund einer Wechsel-Zug-Druck-Spannungszone in der Nähe der Rissspitze kommt es zu einer Rissverzweigung, wie in Bild 6b dargestellt. Es besteht ein Konkurrenzverhältnis zwischen dem koplanaren Risswachstum unter Schubspannung und der Rissverzweigung unter Zugspannung. Das Auftreten von Rissverzweigungen kann durch Überlagerungsspannungen beeinflusst werden. Eine Zugspannung fördert die Rissverzweigung und kann die Ermüdungslebensdauer verkürzen. Eine Druckspannung dagegen ist vorteilhaft, da sie dazu tendiert, die Rissverzweigung zu unterdrücken.
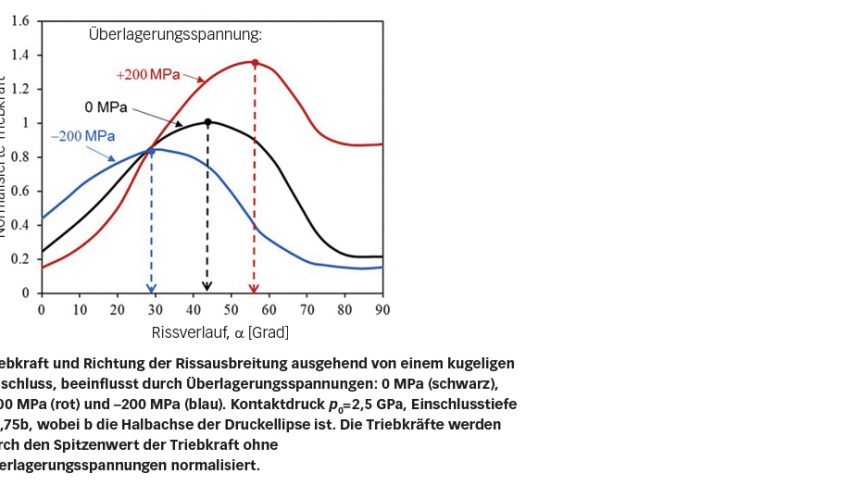
Bild 7 zeigt die Triebkraft für die Rissausbreitung ausgehend von einem kugeligen Einschluss in Abhängigkeit vom Rissverlauf unter Berücksichtigung eines Kontaktdrucks von 2,5 GPa und unterschiedlicher Überlagerungsspannungen. Es wurden die Triebkräfte für Risse mit unterschiedlichem Verlauf ausgewertet. Aus Bild 7 ist ersichtlich, dass die maximale Triebkraft ohne Überlagerungsspannungen einem Rissverlauf von 45° entspricht. Wird eine Druckspannung von 200 MPa angelegt, so erreicht die Triebkraftkurve ihren Höhepunkt in einem Winkel von 30°; bei einer Zugspannung von 200 MPa erhöht sich jedoch der Rissverlauf, bei dem die Triebkraft das Maximum bei 57°erreicht. Es lässt sich also feststellen, dass eine Zugspannung die Rissausbreitung beschleunigen kann und dazu tendiert, das Risswachstum in einen steilen Winkel voranzutreiben, während eine Druckspannung das Risswachstum verlangsamen kann und dazu neigt, die Rissausbreitung in horizontaler Richtung fortzuführen.
Bedeutung aus technischer Sicht
Die Erforschung der Ermüdungsmechanismen hat zur Feststellung einer der Ursachen für das vorzeitige Versagen von Lagern geführt [2]. Der durch weiß anätzende Risse (WECs) und Axialrisse gekennzeichnete Lagerausfall wurde unter anderem in [2] erfolgreich reproduziert, wobei der Innenring eines Zylinderrollenlagers auf einer Hülse mit künstlich eingebrachter Welligkeit montiert wurde. Die FE-Simulation hat gezeigt, dass eine Abweichung der Lagersitzform, wie beispielsweise eine Welligkeit, zu Zugspannungen in der Nähe der Innenringlaufbahn führen kann. Bei Überschreitung einer bestimmten Grenze in Kombination mit der Hertz’schen Spannung führt dies zu einer frühzeitigen Initiierung und beschleunigten Bildung von Rissen im Bereich vorhandener Materialfehler. Dies kann zu einem vorzeitigen Versagen des Lagers führen.
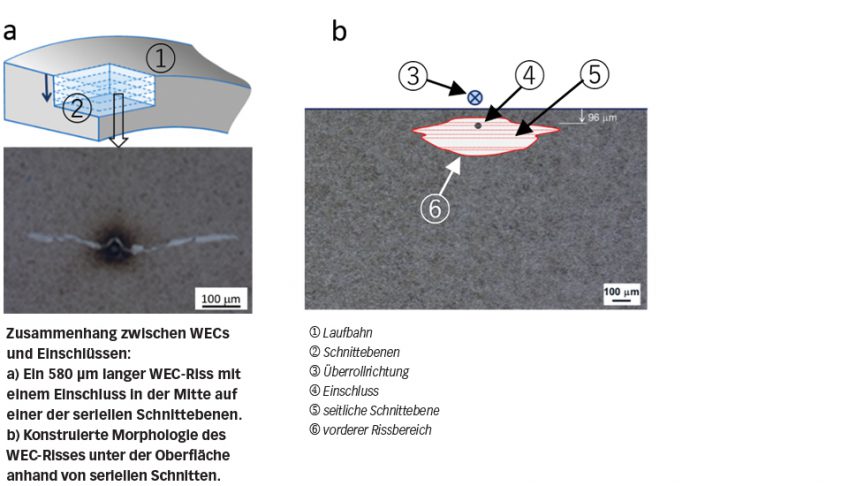
Darüber hinaus zeigte die metallografische Untersuchung der geprüften Lagerringe anhand von kleinstufigen Serienschnitten, dass die in vorzeitig ausgefallenen Lagern häufig anzutreffenden WECs, wie in Bild 8 dargestellt, von Einschlüssen unter der Oberfläche ausgehen können. Eine ähnliche Schlussfolgerung gibt es in der unabhängigen Untersuchung in [4]. Die Bedeutung dieser Erkenntnis liegt in der Klärung der Herkunft der WECs. Ein WEC-Riss ist im Wesentlichen ein Riss unter der Oberfläche, wie beispielsweise ein „Butterfly“, der von einem Spannungserhöher initiiert werden kann, aber in das fortgeschrittene Stadium hineingewachsen ist. Das wiederholte Aneinanderreiben der Rissoberflächen bei Wälzkontaktermüdung führt zu einer allmählich eintretenden Gefügeveränderung, die die Bildung weiß anätzender Zonen (WEAs) in der Nähe der Rissoberflächen zur Folge hat. Daher sind WECs oder WEAs nicht die Ursache für den vorzeitigen Ausfall eines Lagers, sondern Hinweise auf einen fortgeschrittenen RCF-Schaden.
Fazit
Das Erforschen der Ermüdungsmechanismen ist eine grundlegende Voraussetzung für die Weiterentwicklung von Lagersystemen, damit diese den Herausforderungen anspruchsvoller Anwendungen gewachsen sind. Die vorgestellte Forschungsarbeit zeigt, dass durch ein verbessertes Verständnis von Materialfehlern und deren Auswirkungen auf die Lagerleistung neue Möglichkeiten für potenzielle Lösungen entwickelt werden können, um vorzeitige Lagerausfälle zu reduzieren. Darüber hinaus können die Toleranzgrenzen für Materialfehler genauer festgelegt werden.
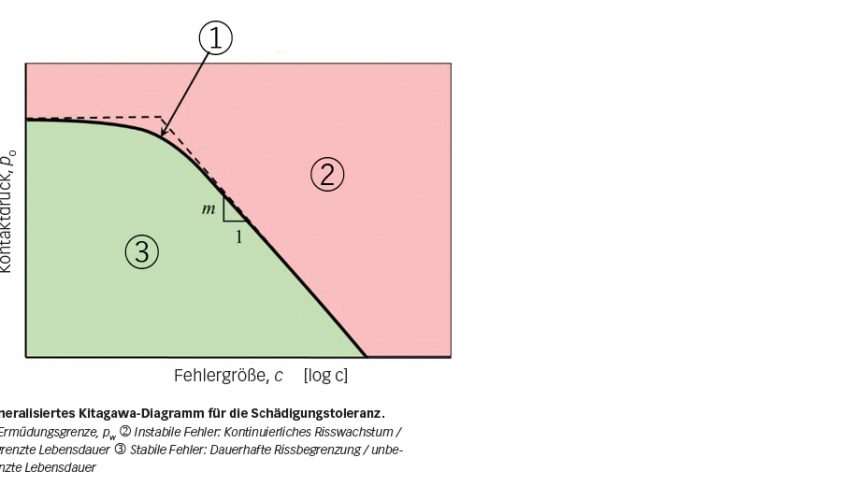
Die Toleranzgrenzen für Materialfehler können anhand eines generalisierten Kitagawa-Diagramms, wie in Bild 9 dargestellt, festgelegt werden. Hier wird die Ermüdungsgrenze in Beziehung zur Fehlergröße und der maximalen Kontaktdruckgrenze gesetzt. Wenn der Fehler verschwindend klein wird, nähert sich die Kurve der intrinsischen Ermüdungsgrenze des Matrixmaterials. Bei großen Fehlern kann die Ermüdungsgrenze durch die Schwellenbedingung für den Beginn des Ermüdungsrisswachstums bestimmt werden, das heißt, die Asymptote mit einer konstanten Steigung von –m, deren Wert von der Art des Fehlers abhängig ist.
Das ursprüngliche Kitagawa-Diagramm [6] wurde für die rissartigen Fehler vorgeschlagen, wobei m = 0,5 ist. Das generalisierte Kitagawa-Diagramm lässt sich auf verschiedene Materialien und Fehlerarten anwenden. So wurde damit beispielsweise die Toleranzgrenze für nicht vorhandenes Material auf der Oberfläche von Siliziumnitrid -Kugeln für Hybridlager festgelegt [6]. Bei dieser Art von Fehler ist m 0,46.
Auf Basis der Beschreibung zur Initiierung und Ausbreitung von Ermüdungsrissen durch Einschlüsse unter der Oberfläche wurde ein Modell entwickelt, welches die Festigkeit und Ermüdungsgrenze von Wälzlagerstählen bei hoher Lastspielzahl (VHCF) berechnen kann [7]. Es konnte nachgewiesen werden [8], dass die vorausberechneten Ermüdungsgrenzen und die VHCF-Prüfdaten gut mit den für die Lebensdauer von Wälzlagern festgelegten Ermüdungsgrenzwerten in ISO 281:2007 übereinstimmen.
Literatur
[1] W. Solano-Alverez, H.K.D.H. Bhadeshia, White-etching matter in bearing steel. Part II: Distinguishing cause and effect in bearing steel failure, Metall. Mater. Trans. A 45A (2014) 4916-4931.
[2] J. Lai, K. Stadler, Investigation on the mechanisms of white etching crack (WEC) formation in rolling contact fatigue and identification of a root cause for bearing premature failure, Wear 364-365 (2016) 244-256.
[3] J.L. Johnson, Contact Mechanics, Cambridge University Press, 1985, Cambridge, UK.
[4] M. Evans, White structure flaking failure in bearings under rolling contact fatigue, PhD Thesis, University of Southampton, UK, 2013.
[5] H. Kitagawa, S. Takahashi, Applicability of fracture mechanics to small cracks or cracks in the early stage. In: Proceedings of the second international conference on mechanical behaviour of materials. ASM, 1976, pp. 627-631.
[6] J. Lai, Y. Kadin, C. Vieillard, Characterization and modelling of the degradation of silicon nitride balls with surface missing-material defects under lubricated rolling contact conditions, Wear 398-399 (2018) 146-157.
[7] J. Lai, T. Lund, K. Ryden, A. Gabelli, I. Strandell, The fatigue limit of bearing steels – Part I: A pragmatic approach to predict very high cycle fatigue strength, Int. J. Fatigue 38 (2012) 155-168.
[8] A. Gabelli, J. Lai, T. Lund, K. Rydén, I. Strandell, G.E. Morales-Espejel, The fatigue limit of bearing steels – Part II: Characterization for life rating standards, Int. J. Fatigue 38 (2012) 169-180.