Periodische Formfehler im Ångström-Bereich (10-10 m) können die Lagerqualität beeinflussen. Sehr bedeutsam sind Abweichungen von der idealen Rundheit der Lagerkomponenten zusammen mit allgemeinen Lagerparametern. Das trifft vor allem für periodisch über den Ringumfang oder die Lauffläche eines Wälzkörpers verteilte Formabweichungen zu. Das eingebaute Lager kann damit zum Ausgangspunkt von Resonanzschwingungen werden.
Durch die Eigenresonanz einiger Systeme kann es bei periodisch wiederkehrenden Formabweichungen an den Lagerteilen zu einer dramatischen Resonanzverstärkung und damit zu Betriebsstörungen kommen. Eine derartige Situation tritt typischerweise dann ein, wenn die Resonanz eine geringe Dämpfung bzw. einen hohen Q-Faktor hat. Die Amplituden im Einbaufall können um Faktoren in der Größenordnung von 1.000 und mehr größer sein als die entsprechende geringe Erreger-Amplitude.
Periodische Formabweichungen bei hochgenauen Lagern, die sog. Welligkeit, liegen im Bereich hoher Ordnungen bei Amplituden von 10-9 m oder sogar 10-12 m und können im Betrieb sehr störende Geräusche verursachen.

Schwingungsformen
Im allgemeinen rufen Welligkeiten drei unterschiedliche Schwingungsformen hervor. Am wenigsten bedeutsam ist die sog. Dehnungsschwingung. Sie tritt bei bestimmten Welligkeiten auf, z.B. wenn die Anzahl der Wellen am Innenring gleich der Wälzkörperanzahl ist. Der Innenring wird dann nach allen Richtungen aufgeweitet, wenn sich alle Wälzkörper gleichzeitig auf den Wellenbergen befinden. Da Außenring und Gehäuse diese Schwingungsform stark unterdrücken, hat sie für die Schwingungserzeugung keine besondere Bedeutung. Anders sieht es im Hinblick auf das Drehmoment aus, worauf allerdings hier nicht eingegangen wird.
Die zweite Schwingungsform, die Biegeschwingung, entsteht, wenn die Differenz zwischen Wellen- und Wälzkörperanzahl gleich 2 ist. Das sich ausbildende Oval erzeugt am Außenring umlaufende Biegeschwingungen, die anders als die Dehnungsschwingungen weniger stark durch Außenring und Lagergehäuse gedämpft werden. Sie sind daher im Hinblick auf die Schwingungserzeugung problematischer.
Am nachteiligsten wirkt sich die dritte Schwingungsform aus. Sie tritt dann auf, wenn sich Wellen- und Wälzkörperanzahl um 1 unterscheiden.
Sobald sich der Wälzkörper im oberen Scheitelpunkt auf einem Wellenberg befindet, erreichen die beiden unteren Wälzkörper ein Wellental. Der Wellenmitte verlagert sich dadurch etwas nach unten. Im nächsten Augenblick ist die Situation umgekehrt, d.h. sie liegt etwas über der idealen Achse.
In diesem Fall übt der Außenring keine dämpfende Wirkung aus. Wenn bei bestimmten Drehzahlen ein Eigenfrequenzbereich erreicht wird, kann es zu beträchtlichen Resonanzschwingungen kommen.

Resonanzerscheinungen
Allgemein kann Resonanz als Austausch von Energie zwischen zwei Energiespeichern bei einer bestimmten Geschwindigkeit betrachtet werden. In der Mechanik läßt sich das an einem Masse-Feder-System veranschaulichen. Wird eine mit einer Feder verbundene Masse ausgelenkt, dann wird die Feder aufgrund der kinetischen Energie der Masse gespannt oder zusammengedrückt, bis die Energie aufgebraucht ist und die Masse zum Stillstand kommt. Dann beschleunigt die Federkraft die Masse in entgegengesetzter Richtung, wobei die potentielle Energie der Feder wieder in kinetische Energie der Masse zurückverwandelt wird. Wenn die höchste Geschwindigkeit der Masse erreicht und die Feder entspannt ist, gibt die Masse erneut ihre Energie an die sich spannende Feder ab.
Der Geschwindigkeitsverlauf entspricht einer Sinuskurve mit bestimmter Periode. Der Reziprokwert der Periodendauer beschreibt die Resonanzcharakteristik des Gesamtsystems und wird als Eigenfrequenz oder natürliche Frequenz (Resonanzfrequenz) bezeichnet. Bei dieser charakteristischen Frequenz muß von außen nur sehr wenig Energie aufgebracht werden, um die Schwingung aufrechtzuerhalten.
Das läßt sich an einem einfachen Beispiel erklären. Ein Vater, der sein auf der Schaukel sitzendes Kind anschiebt, wird dazu nur wenig Kraft aufwenden müssen, wenn er seine Bewegungen der Resonanzfrequenz der schwingenden Schaukel anpaßt.
Mit anderen Worten: eine erregende Kraft kann schon mit sehr wenig Energie ein System zu höchster Resonanz anregen. Einzige Voraussetzung ist, daß das betreffende System bestimmte Resonanzfrequenzen aufweist und die Erregung in Phase mit einer dieser Frequenzen erfolgt. Im Fall der Schaukel ist die Resonanz erwünscht. In Fällen, in denen Lager – selbst mit sehr geringer Welligkeit – zu Schwingungserregern werden könnten, muß dies unbedingt vermieden werden.
Eine Erregung außerhalb der Eigenfrequenzen eines Systems wird nur selten oder nur bei sehr hoher Energie ein Ansprechen des Systems bewirken. Um im Bild zu bleiben: Der Vater würde sich wahrscheinlich verletzen, wenn er die Schaukel gegenphasig mit abweichender Erregerfrequenz anschieben wollte.
Ohne Dämpfung würde in einem schwingenden System die Schwingung nie zum Stillstand kommen. Dämpfung bedeutet, daß einem System Energie entzogen wird, indem sie in eine andere Form, z.B. in Reibungswärme, umgewandelt wird.
Welche Parameter beeinflussen aber nun die Resonanzfrequenz und die mögliche Schwingungsamplitude? Erstens wirkt sich die Massenträgheit aus. Je größer die Masse, desto größer die erforderliche Kraft, um sie zu beschleunigen. Eine größere Masse verschiebt demnach die Resonanz zu niedrigeren Frequenzen hin.
Zweitens ist die Federwirkung zu berücksichtigen, die durch die Federkonstante beschrieben wird: Je größer die Federkonstante, desto größer die Kraft, die die Feder auf eine Masse ausüben kann. Wegen der möglichen größeren Massenbeschleunigung verschieben sich die Resonanzfrequenzen nach oben. Drittens wirken sich Faktoren aus, die zur Dämpfung des Systems beitragen. Meist ist das die Reibung.
Am Beispiel des klassischen Masse-Feder-Systems lassen sich die Einflußparameter in einer Gleichung zusammenzufassen. Wenn man annimmt, daß die Dämpfung gleich Null ist und die Masse durch eine Erregerkraft FA aus der Nullstellung ausgelenkt wird, dann muß FA mit der Rückstellkraft FS der Feder im Gleichgewicht sein:

Sobald keine Erregung mehr stattfindet, würde in einem gedämpften System die Schwingung entsprechend einer fallenden e-Funktion asymptotisch gegen Null gehen. Die Dämpfung hat jedoch keinen Einfluß auf die Resonanzfrequenz.

Lager als Schwingungserreger
In der Praxis können keine exakt runden Laufbahnen hergestellt werden. Beim überrollen werden daher durch die Laufbahn Schwingungen angeregt, die von der Größe und Anzahl der Wellen sowie von der überrollgeschwindigkeit abhängen.
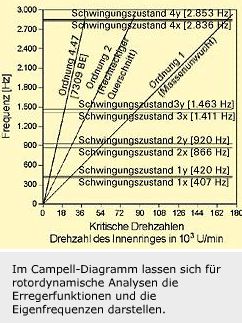
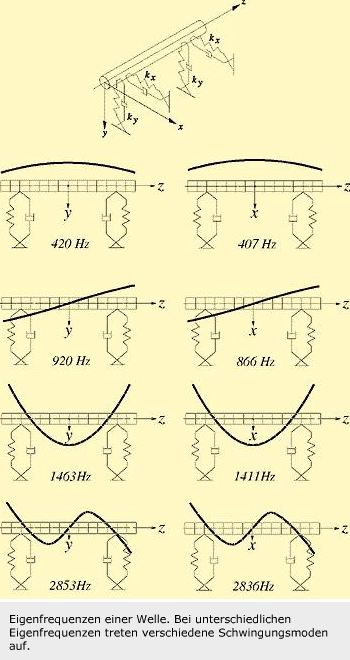
Die Masse, die Steifigkeit und die Eigenfrequenzen von miteinander gekoppelten Teilen spielen eine dominante Rolle. Bei rotordynamischen Analysen wird die Erregerfunktion in einem Campell-Diagramm berücksichtigt.
Berücksichtigt werden auch die Eigenfrequenzen und zugeordneten Schwingungsformen einer elastischen Welle sowie der Einfluß nicht-isotroper Steifigkeitskoeffizienten der Lager. In einem solchen System treten alle Schwingungsmoden bei unterschiedlichen Eigenfrequenzen auf.
Den Eigenfrequenzen entsprechen im Campell-Diagramm die mit ihrer Ordnung gekennzeichneten Waagerechten. Die schräg verlaufenden, mit „Ordnung 1“ usw. bezeichneten Linien stellen die Erregerfaktoren dar, z.B. Unwuchtmasse, Ordnung 1. Die Drehzahlen an den Schnittpunkten sind kritische Drehzahlen. Bei SKF wird das Kennfeld der kritischen Drehzahlen mit einem Computerprogramm berechnet.
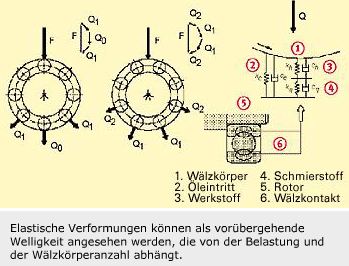
Eine der Welligkeit ähnliche Wirkung haben die elastischen Verformungen aufgrund der Kräfte im Wälzkontakt zwischen Wälzkörpern und Laufbahnen. Die elastische Verformung ist als transiente Welligkeit anzusehen, die von der Belastung und Wälzkörperanzahl oder der Lagersteifigkeit abhängt.
Der Zusammenhang zwischen Rotordynamik und Lagerqualität zeigt, daß ein gutes Lager ein Vorteil, aber keine Gewähr für einwandfreie Funktion ist. Gleichzeitig ist aber auch eine einwandfreie Funktion kein Anzeichen für hohe Lagerqualität. Es kann sich auch nur um ein glückliches Zusammentreffen von Rotoreigenschaften und Unvollkommenheiten der Lager handeln.

Eine Fallstudie
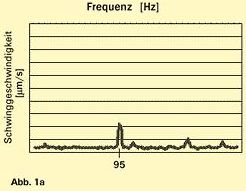
Wenn eine sog. Maske benutzt wird, können während der Produktion Lager ausgewählt werden, die bei kritischen Resonanzen weniger schwingungsanregend wirken. Abb. 1 zeigt das am praktischen Beispiel von zwei Lagern in einer Maschine. Bei Messungen mit einem Schwingungsprüfer bei 700 U/min (11,66 Hz) wird für Lager 1 (Abb. 1a) aufgrund seiner Welligkeit eine ziemlich geringe Schwingungsneigung , aber eine relativ große Amplitude bei etwa 95 Hz festgestellt.
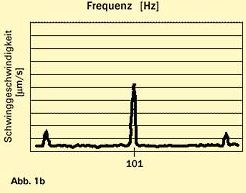
Bei Lager 2 (Abb. 1b) ist die Amplitude 2,5mal größer, liegt allerdings bei 101 Hz. Eigentlich sollte Lager 1 geräuschärmer laufen. Die Betriebsdrehzahl der Maschine liegt bei 3.600 U/min (60 Hz). Lager 2 lief einwandfrei, bei Lager 1 dagegen zeigte sich ein störender Schwingungsausschlag, der mit einer Eigenfrequenz der Welle bei 488,5 Hz (95/11,66 = 488,5/60 = Ordnung 8,14) zusammenfiel. Ursache ist eine Welligkeit mit sehr kleiner Amplitude.
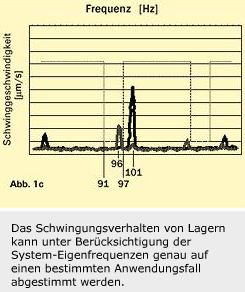
Um Resonanzen bei der kritischen Drehzahl zu vermeiden, könnte bei Benutzung einer Maske die Schwingungserregung bei dieser Frequenz eingeschränkt werden. Dafür muß die Welligkeit, die Schwingungen bei 95 Hz anregt, begrenzt werden. Besser ist es, die Grenze in einen Bereich zu legen, z.B. zwischen 91 und 97 Hz, um Drehzahlschwankungen, geometrische Abweichungen und Belastungsunterschiede zu berücksichtigen (Abb. 1c).
Erfahrungsgemäß folgt aus der Benutzung von Masken eine Welligkeits-Spezifikation entsprechend Abb. 2.
Bei einer Maschinendrehzahl von 3.000 U/min (50 Hz) würde sich eine Ordnung 9,77 = 488,5/50 ergeben. Das würde einer Erregung bei 407 Hz entsprechen, also einem resonanzfreien Zustand. Lager 1 würde einwandfrei laufen, weil 407 Hz unterhalb der Eigenfrequenz von 488,5 Hz liegt.
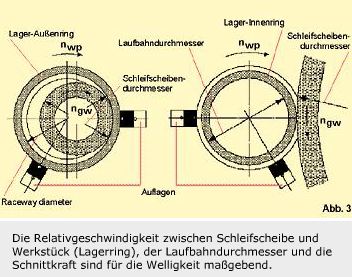
Abb. 3 zeigt, daß die Relativgeschwindigkeit zwischen Schleifscheibe und Werkstück (Lagerring), der Laufbahndurchmesser und die Schnittkraft maßgebend für die Welligkeit sind. Eine Vorverformung des Ringes und die Steifigkeit der Abstützung (Schleifspindel und Auflagen) beeinflussen die Schnittkraftschwankungen und Schwingungen bei der Bearbeitung, die sich als Abweichungen von der Idealform (Welligkeit) auswirken.
Welligkeit kann durch folgende Bearbeitungsverfahren verursacht sein:

Wärmebehandlung führt i.a. zu Ovalität, d. h. zwei Wellen am Umfang (2. Ordnung)
Spitzenlosschleifen oder Drehen mit Dreibackenfutter ergibt ein typisches Reuleaux-Dreieck, d.h. drei Wellen am Umfang (3. Ordnung)
Drehen mit Vierbackenfutter ergibt ein Viereck, d.h. vier Wellen am Umfang (4. Ordnung)
Welligkeiten höherer Ordnung ergeben sich normalerweise aus dem Verhältnis der Geschwindigkeiten von Schleifscheibe und Lagerring oder aus störenden Maschinenresonanzen.

Anschließendes Honen beeinflußt hauptsächlich die Größe der Welligkeit. Höhere Ordnungen werden dabei beträchtlich reduziert, niedrigere bleiben erhalten oder werden sogar vergrößert.

Folgerung
Standardfertigung läßt Welligkeitswerte um 28 µm/s im Hochband z.B. für ein Lager 7309 BE zu. Bei der Fertigung von Hochpräzisionslagern, die durch optimierte Bearbeitungsgeschwindigkeiten und eine besondere qualitätsbezogene vorbeugende Wartung gekennzeichnet ist, werden die Welligkeitswerte für die gleiche Lagergröße um den Faktor 1,5 bis 3 reduziert.
Unter Berücksichtigung einer gleichmäßig harmonischen Verteilung im Filterband und einer Drehzahl von 183 U/min, darf z.B. eine Welligkeit mit 200 Wellen am Umfang gerade einmal eine wegproportionale Amplitude von 0,46 nm haben, was vernachlässigbar erscheint.
So unglaublich es klingt, kann aber im Realfall eine Welligkeit im Nanometerbereich starke Schwingungen hervorrufen, wenn die Anregung in der Nähe der Eigenfrequenz erfolgt.

Hubert Köttritsch und Franz Reithuber,  
SKF Österreich AG, Steyr, Österreich