Optimale Einsatzhärtungstiefe für die Lagerleistung

Die Kontaktflächen von Lagern werden zur Erhöhung der Verschleißfestigkeit und der Tragfähigkeit speziellen Wärmebehandlungen unterzogen. Dabei werden die Bauteile, unter anderem je nach Lagergröße und verwendeter Stahlsorte, entweder durchgehärtet oder oberflächengehärtet. Bei Stählen mit hohem Kohlenstoffgehalt ist Durchhärtung geeignet, während Stähle mit niedrigem Kohlenstoffgehalt (< 0,25 % Kohlenstoff) Einsatzhärtung erfordern, die beispielsweise durch Aufkohlung erzielt wird. Ein weiteres gängiges Härtungsverfahren für Stähle mit mittlerem Kohlenstoffgehalt ist das Induktionshärten.

Beim Aufkohlen wird Kohlenstoff bei hoher Temperatur in kohlenstoffarmen Stahl eindiffundiert und beim Abschrecken bildet sich dann eine einsatzgehärtete Randschicht. Die Tragfähigkeit von oberflächengehärteten Lagern hängt unter anderem von der Einsatzhärtungstiefe und der Kernfestigkeit ab. Die Lagerhersteller müssen die Stahlsorten sorgfältig auswählen und eine ausreichende Einsatzhärtungstiefe für die jeweiligen Anwendungen sicherstellen. Allerdings treibt eine zu große Einsatzhärtungstiefe nicht nur die Herstellungskosten unnötigerweise in die Höhe, sondern kann auch zu einer Rissbildung während des Härtens und zu unerwünschten Erscheinungen wie intergranulare Oxidation und vergrößerte Körnung führen. [1].

Ein Durchdrücken des Kerns [2, 3], eine Ausfallart bei oberflächengehärteten Lagern, tritt aufgrund einer zu geringen Einsatzhärtungstiefe oder einer zu hohen Kontaktbelastung oder einer Kombination aus beidem auf. Hierbei kommt es im Werkstoffkern unter der gehärteten Randschicht zur Bildung und Ausbreitung von Rissen. Der Härteunterschied zwischen der Randschicht und dem Kern trägt erheblich zum Durchdrücken des Kerns bei, da die Beanspruchung durch den Rollkontakt die statische Festigkeit oder die Dauerfestigkeit des Kerns übersteigen kann. In Studien von Alfredsson und Olsson [4] und Lai et al. [5] wurde bei oberflächengehärteten Proben, die einer Ermüdungsbelastung bei Stillstand (Standing Contact Fatigue, SCF) ausgesetzt waren, ein Durchdrücken des Kerns beobachtet. Bei der SCF-Prüfung wird die Oberfläche eines Prüflings mit einer Kugel oder Rolle zyklisch eingedrückt. Numerische Simulationen [5] ergaben, dass geringe Einsatzhärtungstiefen oder zu hohe Kontaktbelastungen zu erheblichen Zugeigenspannungen im Übergangsbereich zwischen Randschicht und Kern führen, die unter SCF-Belastung die Bildung von Querrissen zur Folge haben. Eine starke Plastizität im Kern schwächt die Unterstützung der Randschicht durch den Kern, was zu einer Durchbiegung der Randschicht und eventuell zu Rissen führt, wenn die Belastungsgrenzen überschritten werden. Neben dem Durchdrücken des Kerns zeigt sich die statische Tragfähigkeit von oberflächengehärteten Lagern auch in der plastischen Verformung bei stationärer Kontaktbelastung. Die in ISO 76 [6] definierte statische Tragzahl bezieht sich jedoch nicht auf oberflächengehärtete Lager. Es wurden Berechnungsmethoden [5] zur Bewertung der plastischen Laufbahneindrückungen bei induktionsgehärteten Drehverbindungen vorgeschlagen.

Dieser Artikel basiert auf einer kürzlich von uns veröffentlichten Studie [7], die zum Ziel hatte, das Werkstoffverhalten einsatzgehärteter Lager unter SCF-Bedingungen zu charakterisieren und zu modellieren. Durch die Bewertung plastischer Oberflächeneindrückungen und des Risikos eines Durchbrechens des Kerns bietet diese Untersuchung interessante Erkenntnisse für Konstrukteure und Hersteller, insbesondere im Hinblick auf die Leistungsoptimierung von einsatzgehärteten Lagern.

Numerische Simulation und Modellierung

Mit der Finite-Elemente-Analyse (FEA) und dem kommerziellen Programm ABAQUS wird die Wechselwirkung zwischen einem Wälzkörper und der Laufbahnoberfläche eines einsatzgehärteten Lagerrings simuliert. Die Simulation umfasst drei Kontaktarten: Punktkontakt (PC), Linienkontakt (LC) und elliptischer Kontakt (EC).

Angesichts der Tatsache, dass unser Fokus auf dem Verständnis der Werkstoffreaktion auf eine Kontaktbelastung bei Stillstand liegt, ist das elastisch-plastische Werkstoffverhalten für das FE-Modell von entscheidender Bedeutung. Die Beschreibung der elastisch-plastischen Verformung erfolgt über den Spannungs-Dehnungs-Zusammenhang, der typischerweise aus Zug- oder Druckversuchen abgeleitet wird. Da die Festigkeit des Werkstoffs sehr stark von der Härte abhängig ist, korrelieren wir den Festigkeitsgradienten des aufgekohlten Bauteils mit dem Härteprofil. Durch die Erstellung von Spannungs-Dehnungs-Kurven für das Kerngefüge und die gehärtete Randschicht anhand von Druckversuchen können wir durch lineare Interpolation den Spannungs-Dehnungs-Zusammenhang für Werkstoffe mit beliebiger Härte näherungsweise bestimmen.

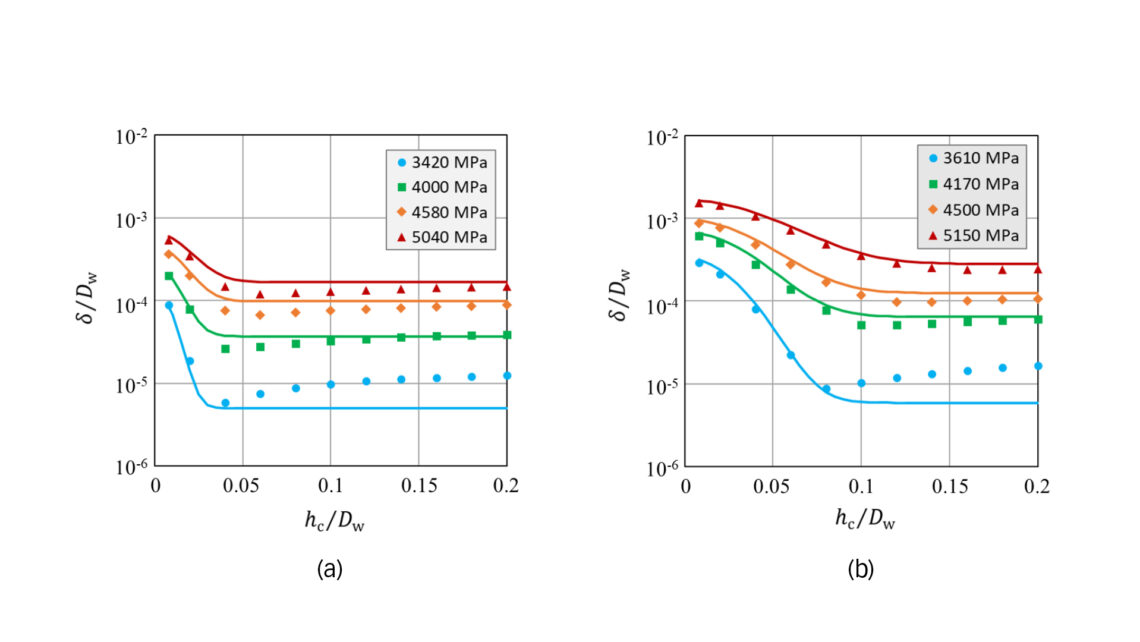
Das FE-Modell erleichtert die Beurteilung der plastischen Eindrückungen an der Oberfläche und der Schädigung unter der Oberfläche infolge einer Kontaktbelastung bei Stillstand. Von einer Parameterstudie, die verschiedene Belastungen und Härteprofile umfasst, leiten wir empirische Gleichungen ab, die die plastische Laufbahnverformung in Abhängigkeit von der Einsatzhärtungstiefe, der Einsatz- und Kernhärte, dem Wälzkörperdurchmesser und dem Kontaktdruck angeben. Überdies ermöglicht die Studie die Festlegung von Toleranzgrenzen für Schädigungen unter der Oberfläche bei einsatzgehärteten Lagerringen, die einer Kontaktbelastung bei Stillstand ausgesetzt sind.

Betrachten wir ein Bauteil mit gleichmäßiger Härteverteilung, ähnlich dem Durchhärten oder dem Kerngefüge vor dem Aufkohlen. Die plastischen Eindrückungen an der Oberfläche (δ) hängen mit dem maximalen Kontaktdruck (p₀) und der Dehngrenze des Werkstoffs (σ_y) wie folgt zusammen:

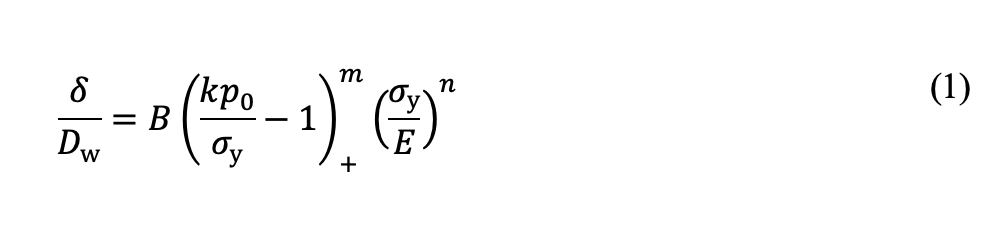
D_w ist der Wälzkörperdurchmesser und (…)+ steht für die McCauley-Einschränkung, die den Term auf null setzt, wenn die eingeschlossene Größe negativ ist. Die werkstoffunabhängige Konstante k verbindet den Kontaktdruck p₀ und die maximale von-Mises-Spannung σ_vM (σ_vM = kp₀). Beim Punktkontakt (PC) ist k = 0,62 und beim Linienkontakt (LC) ist k = 0,56. Die Konstanten B, n und m sind werkstoffspezifisch.

Beim Aufkohlen und Härten des Bauteils entstehen plastische Eindrückungen durch die Verformung der Randschicht und des Kerns. Die Aufteilung zwischen diesen Bereichen ist abhängig von der relativen Einsatzhärtungstiefe (h_c /D_w). Die Einsatzhärtungstiefe h_c ist hier definiert als die Tiefe, bei der die Härte gleich HV550 ist. Nach Lai et al. [5]:

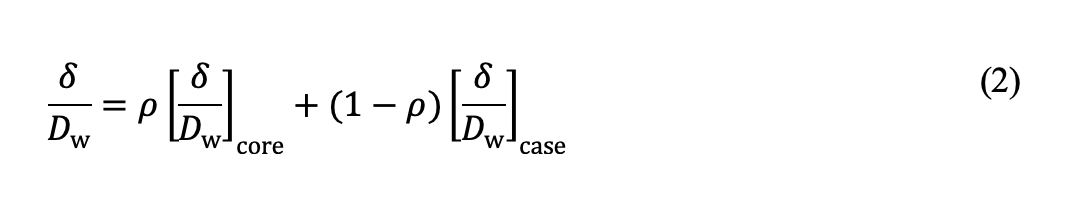
[δ /D_w]_case und [δ /D_w]core sind die entsprechenden plastischen Eindrückungen beim Werkstoff der Randschicht (case) und des Kerns (core) nach Gleichung (1). Der Aufteilungsparameter ρ in der oben stehenden Gleichung ist abhängig von der relativen Einsatzhärtungstiefe h_c /D_w und dem Kontaktdruck:

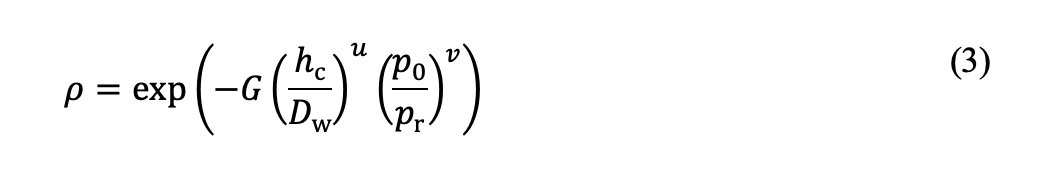
p_r ist ein auf 1.000 MPa eingestellter Bezugsdruck. Die Konstanten G, u und v werden bestimmt, indem die aus FE-Berechnungen gewonnenen Daten für die plastischen Eindrückungen in die Gleichungen (2) und (3), wie in Bild 1 dargestellt, eingesetzt werden. Man beachte, dass die statische Tragzahl für durchgehärtete Lager definiert ist als der Kontaktdruck, der einer plastischen Eindringtiefe an der Oberfläche von 10^-4D_w [6] entspricht.

Die durch ellipsenförmigen Kontakt bedingten plastischen Eindrückungen [δ /D_w]_EC ergeben sich durch Interpolation basierend auf dem b /a-Verhältnis zwischen Lösungen für Punkt- und Linienkontakte:

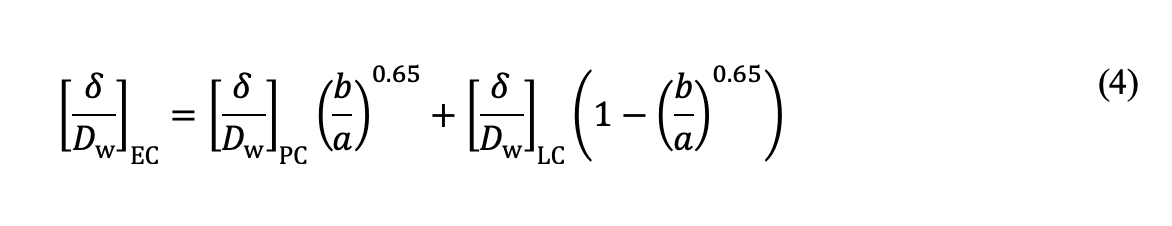
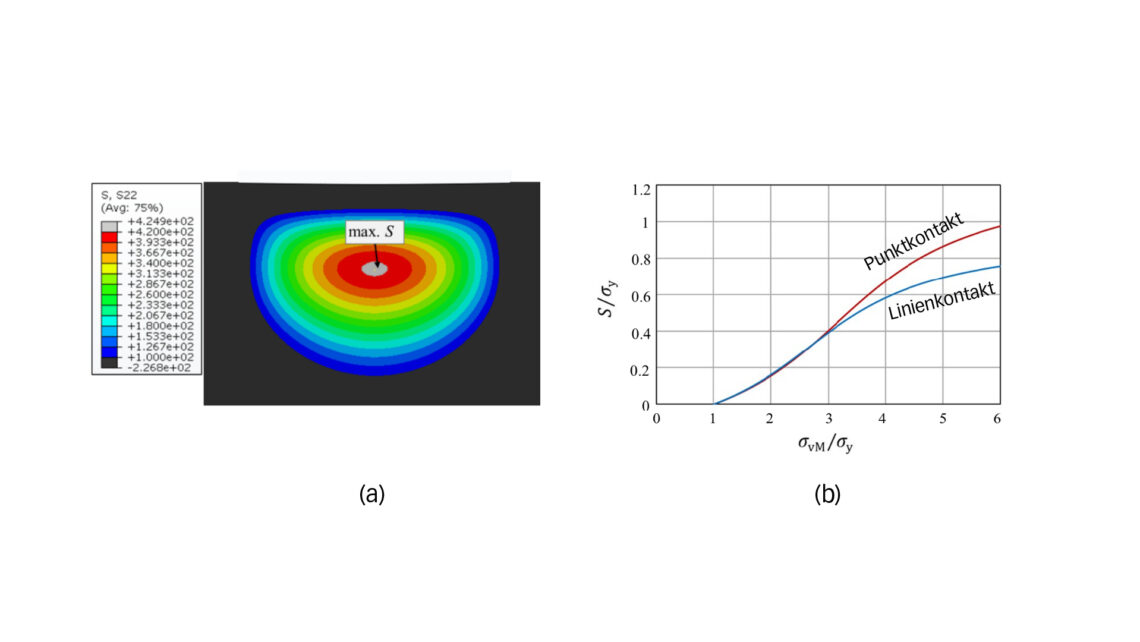
Mit Hilfe der FE-Analyse untersuchen wir das Werkstoffverhalten hinsichtlich plastizitätsinduzierter Eigenspannungen. Sobald die Spannung infolge einer statischen Belastung die Dehngrenze des Kernwerkstoffs übersteigt, tritt plastisches Fließen auf, was zu einer Werkstoffschädigung unter der Oberfläche in Form von Eigenspannung führt. Bild 2a zeigt eine Zugeigenspannungszone im Übergangsbereich zwischen Randschicht und Kern, die durch eine hohe Kontaktspannung entsteht. Ein vergleichbares Eigenspannungsmuster wurde bei induktionsgehärteten Teilen festgestellt, die einem Kugel- oder Rolleneindruck ausgesetzt waren, wie in einer früheren Studie dargelegt wurde [5]. Diese Studie hat gezeigt, dass unter SCF-Belastung Zugeigenspannungen Risse oder Delamination an der Schnittstelle Randschicht-Kern verursachen können.

Der Ausdruck für die Eigenspannung unter der Oberfläche infolge Kontaktbelastung bei Stillstand, der bereits aufgestellt wurde [5], lässt sich auf einsatzgehärtete Bauteile wie folgt anwenden:

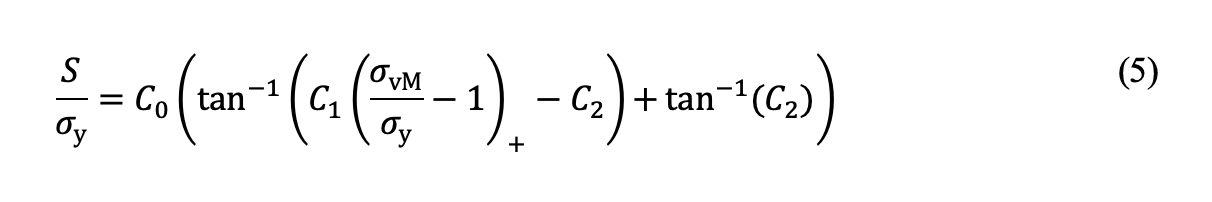
Hier entspricht σ_y der Dehngrenze des Kernwerkstoffs, σ_vM ist die entsprechende von-Mises-Spannung in einer Tiefe h_c von der Oberfläche ausgehend oder in der Tiefe, in der die Härte HV550 entspricht. C0, C1 und C2 sind Konstanten, die durch Einsetzen der FE-Ergebnisse in die Gleichung (5) bestimmt werden können. Zu beachten ist, dass die von-Mises-Spannung hier nach der Hertz’schen Theorie des elastischen Kontakts bewertet wird, die die Spannungslösung unter die Annahme linearer Elastizität stellt. Bild 2b zeigt die Zugeigenspannungen in Abhängigkeit von der entsprechenden von-Mises-Spannung in einer Tiefe h_c von der Oberfläche ausgehend, und zwar bei Linien- bzw. Punktkontakt. Die kritische Spannung S_c kann anhand der Prinzipien der Bruchmechanik und des Ansatzes von El Haddad [8] zur Berücksichtigung der Auswirkungen kleiner Risse, wie er in einer früheren Veröffentlichung [5] beschrieben wurde, bewertet werden.

Versuch und Modellüberprüfung

Es wurden SCF-Tests an einem flachen Prüfling aus ASTM A534-18NiCrMo14-6 durchgeführt. Zwei Scheibenproben wurden aufgekohlt und anschließend gehärtet, was zwei Härteprofile mit Einsatzhärtungstiefen von 0,50 mm bzw. 0,90 mm ergab. Bei der SCF-Prüfung wurde ein balliger Rolleneindrückkörper mit einem Durchmesser von 10 mm und einem Krümmungsradius von 98 mm aus martensitgehärtetem Stahl (ASTM A295-52100) verwendet. Direkt neben dem eingedrückten Bereich wurden Dehnungsmessstreifen angebracht, um Dehnungsänderungen während der Tests verfolgen zu können. Es wurde festgestellt [4], dass eine plötzliche Zunahme der Dehnung auf die Bildung eines Querrisses in der Übergangszone zwischen Randschicht und Kern hinweist, und dass dies als Nachweis für ein Durchdrücken des Kerns unter SCF-Belastung bei einem oberflächengehärteten Bauteil angesehen werden kann.

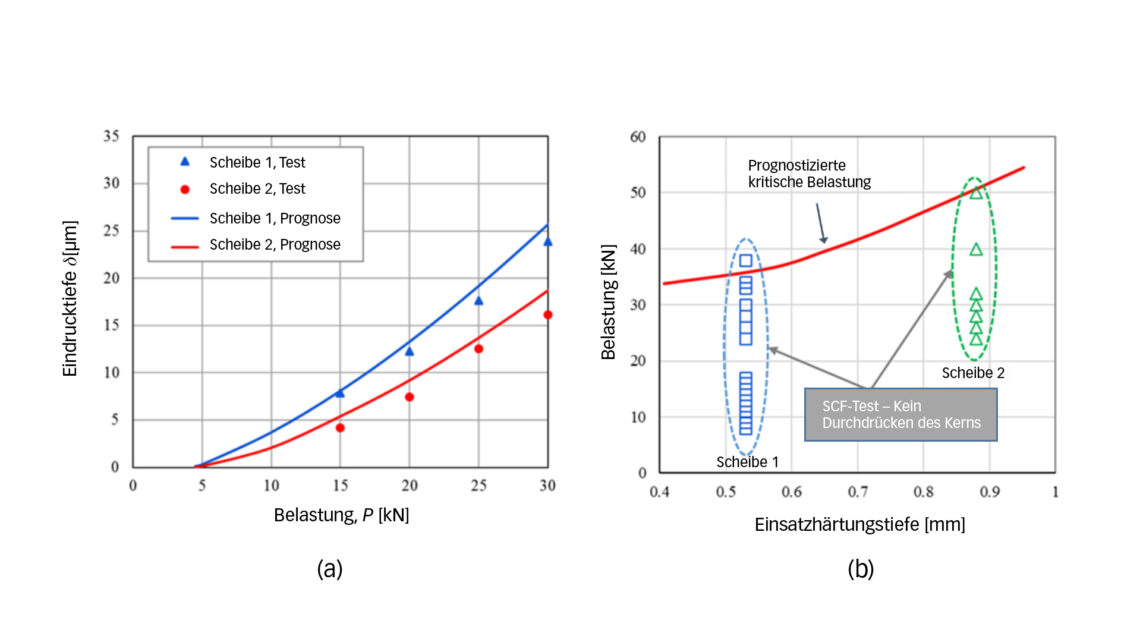
Bild 3a zeigt die gemessenen plastischen Eindrückungen im Vergleich zu den Modellprognosen unter Verwendung der Gleichungen (1) – (4) und weist auf eine gute Übereinstimmung zwischen Prognosen und Versuch hin.

Bei allen Tests mit beiden Scheiben und unterschiedlichen Belastungen konnten anhand der Dehnungsmessstreifen keine Hinweise auf eine Querrissbildung in den Bereichen unter der Oberfläche festgestellt werden. Metallographische Untersuchungen nach den Tests bestätigten, dass sich keine Querrisse in den Bereichen unter der Oberfläche der geprüften Scheiben gebildet hatten. Bild 3b zeigt alle SCF-Tests unterteilt nach Scheibe 1 und Scheibe 2 mit den jeweiligen Einsatzhärtungstiefen. Die kritische Last für das Durchdrücken des Kerns, die auf die Bildung eines Querrisses unter der Oberfläche hinweist, wurde berechnet und in Bild 3b dargestellt. Die Modellprognose wird als plausibel angesehen, da fast alle experimentellen Datenpunkte, die kein Durchdrücken des Kerns anzeigen, unterhalb der prognostizierten kritischen Belastungen liegen. Der einzige Datenpunkt, der leicht über der prognostizierten kritischen Belastung liegt, deutet auf eine konservative Modellprognose hin. Bei den SCF-Tests wurden beide Scheiben mit extrem hohen Belastungen hinsichtlich des nominellen Kontaktdrucks geprüft. So entspricht die höchste Belastung von Scheibe 1 einer Hertz’schen Pressung von 7,10 GPa, während der maximale Kontaktdruck bei Scheibe 2 7,70 GPa beträgt. Gegenüber induktionsgehärteten Bauteilen [5] scheint der einsatzgehärtete Stahl in dieser Studie aufgrund seiner Eigenschaften weniger anfällig für das Durchdrücken des Kerns zu sein.

Statische Eindruckversuche wurden auch an der Laufbahnoberfläche eines Zylinderrollenlagers (CRB) durchgeführt. Bei dem Prüfling handelte es sich um ein aus dem Innenring des Zylinderrollenlagers geschnittenes Segment aus einsatzgehärtetem Stahl (ASTM A534-18NiCrMo14-6). Durchgehärtete Zylinderrollen mit unterschiedlichen Durchmessern wurden als Eindruckkörper verwendet, um Belastungen mit unterschiedlichen relativen Einsatzhärtungstiefen hinsichtlich des h_c / D_w-Verhältnisses zu erhalten.

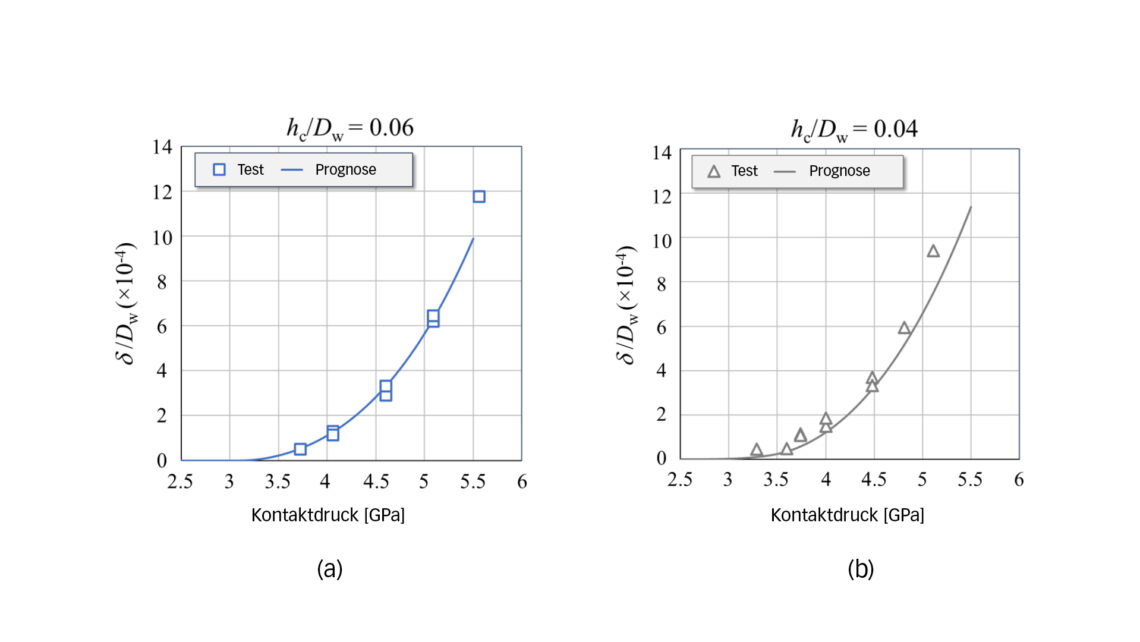
Bild 4 zeigt die plastischen Eindrückungen für zwei relative Einsatzhärtungstiefen, die durch Messung bzw. Prognose unter Verwendung der Gleichungen (1) – (4) ermittelt wurden. Dabei lässt sich eine recht gute Übereinstimmung zwischen dem Versuch und der Modellprognose feststellen.

Concluding remarks

In conclusion, this study delved into the material response of case-carburized rings under SCF loading, employing a combination of numerical simulations and experimental investigations. By focusing on surface plastic indentation and subsurface core crushing, our finite element-based models accurately predicted material damage and deformation behaviour. Validation through SCF tests on both a carburized block and inner ring of a cylindrical roller bearing confirmed the model’s reliability. This work not only enhances understanding but also offers a practical method for assessing the performance of case-carburized bearings in standing contact conditions, with potential implications for optimizing design and durability in engineering applications.