Profondeur de carburation optimale pour les performances du roulement

Les surfaces de contact des roulements sont soumises à des traitements thermiques spécifiques destinés à accroître leur résistance à l’usure et leur capacité de charge. En fonction de certains facteurs, tels que la taille des roulements et les nuances d’acier utilisées, les composants peuvent être soumis à une trempe à cœur ou superficielle. La trempe à cœur convient aux aciers à haute teneur en carbone, tandis que les aciers à faible teneur (< 0,25 % de carbone) nécessitent d’être cémentés par le biais de procédés comme la carburation. La trempe superficielle par induction constitue une autre méthode, couramment utilisée pour les aciers à teneur moyenne en carbone.

La carburation des aciers à faible teneur en carbone consiste à diffuser une source de carbone dans l’acier à une température élevée pour former une couche superficielle durcie lors de la trempe. La capacité de charge des roulements durcis en surface dépend de facteurs tels que la profondeur de trempe et la résistance du matériau du cœur. Les fabricants de roulements doivent sélectionner soigneusement les nuances d’acier et garantir une profondeur de trempe adaptée aux applications spécifiques. Une profondeur de trempe excessive peut en revanche entraîner non seulement des coûts de fabrication superflus, mais également la formation de fissures lors du durcissement, ainsi que d’autres effets indésirables, tels qu’une oxydation intergranulaire et une hypertrophie des grains [1].

L’écrasement du cœur [2, 3], qui constitue un mode de défaillance des roulements durcis en surface, résulte d’une profondeur de cémentation insuffisante, de charges de contact excessives ou d’une combinaison de ces deux causes. Cette défaillance se traduit par le déclenchement et la propagation de fissures dans le matériau du cœur sous la couche durcie. L’écart de dureté entre la couche de surface et le cœur contribue de manière significative à l’écrasement du cœur, puisqu’il entraîne des contraintes au niveau du contact roulant qui peuvent dépasser la résistance statique ou la résistance à la fatigue du cœur. Des études menées par Alfredsson et Olsson [4] et Lai et al. [5] ont observé un écrasement du cœur dans des échantillons durcis en surface soumis à des conditions de charge de fatigue de contact fixe (FCF). Le test FCF consiste en l’indentation cyclique de la surface d’un échantillon à l’aide d’une bille ou d’un rouleau. Des simulations numériques [5] ont révélé que de faibles profondeurs de cémentation ou des charges de contact excessives induisent une contrainte résiduelle de traction importante au niveau de la zone de transition entre la couche en surface et le cœur qui est à l’origine de la formation de fissures latérales sous charge de fatigue de contact fixe. Une plasticité importante dans le cœur fragilise le support offert à la couche cémentée qui, par conséquent, est sujette à une courbure et une fissuration potentielle en cas de dépassement des limites de contrainte. Outre l’écrasement du cœur, la capacité de charge statique des roulements durcis en surface est fonction de la déformation plastique sous des charges de contact fixe. Cependant, la définition de la charge statique dans la norme ISO 76 [6] ne tient pas compte des roulements durcis en surface. Des méthodes de calcul [5] ont été proposées pour évaluer l’indentation plastique du chemin de roulement dans les roulements d’orientation durcis en surface par induction.

Cet article est basé sur une étude que nous avons publiée récemment [7], visant à caractériser et à modéliser le comportement du matériau des roulements en acier carburé dans des conditions de FCF. L’étude de l’indentation plastique de la surface et du risque d’écrasement du cœur fournit aux concepteurs et fabricants des informations utiles pour optimiser les performances des roulements en acier carburé.

Simulation et modélisation numériques

L’interaction entre un élément roulant et la surface du chemin de roulement dans une bague de roulement carburée est simulée au moyen d’une analyse par éléments finis (EF) réalisée avec le logiciel commercial ABAQUS. La simulation englobe trois types de contacts : contact ponctuel (CP), contact linéaire (CL) et contact elliptique (CE).

Puisque c’est la réponse du matériau aux charges de contact fixe qui nous intéresse, le comportement élastique et plastique du matériau occupe une place centrale dans le modèle par EF. La description de la déformation élastoplastique englobe la relation contrainte-déformation, généralement fournie par des tests de tension ou compression. La résistance du matériau étant étroitement liée à la dureté, nous établissons une corrélation entre le gradient de résistance dans le composant carburé et le profil de dureté. À travers les courbes contrainte-déformation élaborées pour la structure du cœur et pour la structure de la couche durcie à partir de tests de compression, nous appliquons l’interpolation linéaire pour approcher la relation contrainte-déformation pour un matériau de n’importe quelle autre dureté.

Le modèle par EF facilite l’évaluation de l’indentation plastique de la surface et des dommages internes résultant de charges de contact fixe. À partir d’une étude paramétrique englobant diverses conditions de charge et profils de dureté, nous déduisons des équations empiriques pour exprimer la déformation plastique du chemin de roulement en fonction de la profondeur de cémentation, de la dureté de la couche durcie et du cœur, du diamètre des éléments roulants et de la pression de contact. L’étude permet en outre d’établir des limites de tolérance pour les dommages internes dans les bagues de roulement carburées soumises à des conditions de charge de contact fixe.

Prenez un composant de dureté uniforme comme c’est le cas après une trempe à cœur ou pour la structure du cœur avant carburation. L’indentation plastique de la surface (δ) est liée à la pression de contact maximale (p₀) et à la limite d’élasticité du matériau (σ_y), selon la formule suivante :

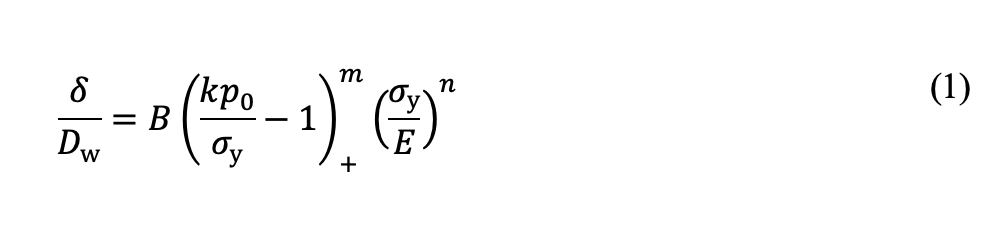
Dans cette formule, D_w correspond au diamètre de l’élément roulant et (…)+ indique l’utilisation de crochets de McCauley, ce qui signifie que le terme entre crochets passe à zéro si la quantité à laquelle il se rapporte est négative. La constante k, indépendante des matériaux, met en relation la pression de contact p₀ et la contrainte de von Mises maximale σ_vM (σ_vM = kp₀). Pour le contact ponctuel (CP), k = 0,62, et pour le contact linéaire (CL), k = 0,56. Les constantes B, n et m sont spécifiques au matériau.

Si le composant est soumis à une carburation et une trempe, l’indentation plastique résulte à la fois de la déformation de la couche durcie et de celle du cœur. La répartition entre ces deux contributions dépend de la profondeur de cémentation relative (h_c /D_w). Ici, la profondeur de cémentation h_c est définie comme la profondeur à laquelle la dureté est égale à HV550. D’après Lai et al. [5] :

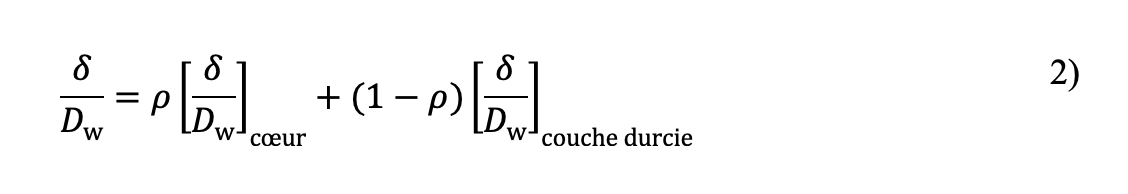
où [δ /D_w]_couchedurcie et [δ /Dw]_cœur correspondent aux indentations plastiques des matériaux de la couche durcie et du cœur, respectivement, données par l’éq. 1. Le paramètre de répartition ρ dans l’équation ci-dessus est fonction de la profondeur de cémentation relative h_c /D_w et de la pression de contact :

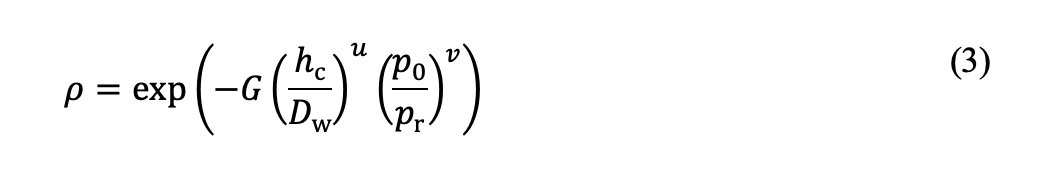
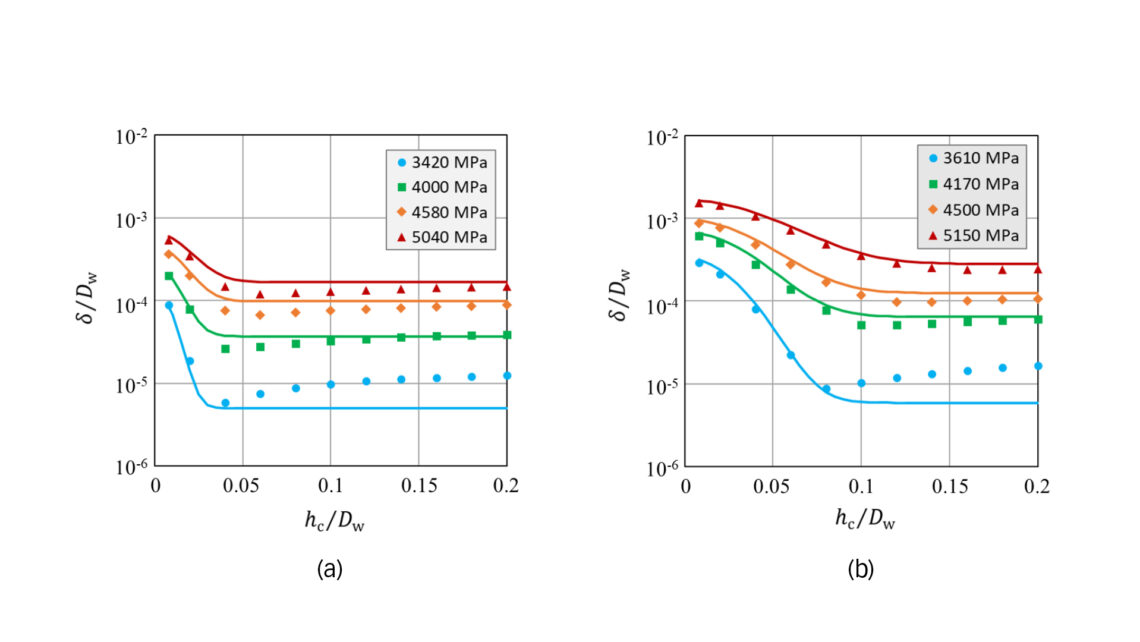
où p_r est une pression de référence de 1 000 MPa. Les constantes G, u et v sont déterminées en appliquant l’éq. 2) associée à l’éq. 3) aux données d’indentation plastique obtenues à partir des calculs par EF, comme illustré sur la fig. 1. Il convient de noter que la charge statique nominale des roulements trempés à cœur est définie comme la pression de contact qui correspond à une profondeur d’indentation plastique de surface de 10-4D_w [6].

L’indentation plastique de contact elliptique [δ /D_w]_CE résulte d’une interpolation basée sur le rapport b /a entre solutions pour contacts ponctuels et pour contacts linéaires :

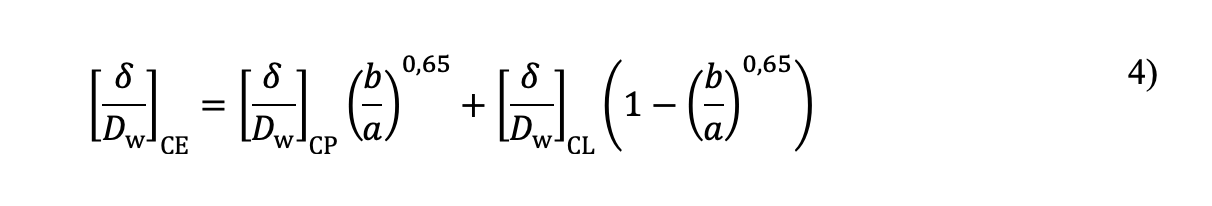
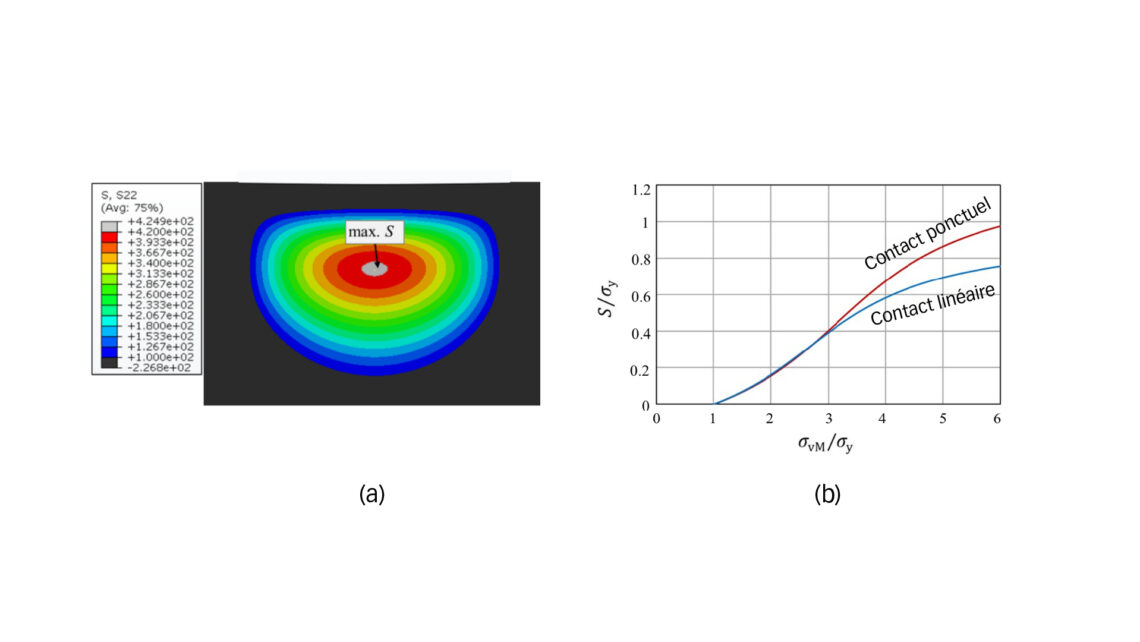
L’analyse par EF nous permet d’étudier la réponse du matériau en ce qui concerne la contrainte résiduelle induite par la plasticité. Lorsque la contrainte résultant d’une charge statique dépasse la limite d’élasticité du matériau du cœur, un écoulement plastique se produit, causant des dommages au matériau de sous-couche sous forme de contrainte résiduelle. La fig. 2a représente une zone de contrainte résiduelle de traction dans la région transitoire surface durcie-cœur résultant d’une contrainte de contact élevée. Un modèle de contrainte résiduelle comparable a été identifié dans des pièces durcies en surface par induction soumises à une indentation par des billes ou rouleaux, comme démontré dans une précédente étude [5]. Cette étude révèle que, dans des conditions de charge FCF, la contrainte résiduelle de traction peut induire une fissuration ou un délaminage à l’interface entre la couche durcie et le cœur.

L’expression de la contrainte résiduelle de traction interne due à une charge de contact fixe, précédemment établie [5], s’avère applicable aux composants carburés :

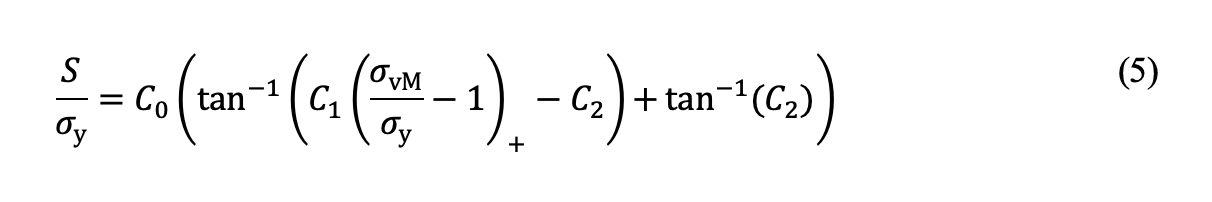
dans laquelle σ_y est la limite d’élasticité du matériau du cœur, σ_vM est la contrainte de von Mises équivalente à une profondeur h_c par rapport à la surface ou à la profondeur à laquelle la dureté est égale à HV550. Les constantes C₀, C₁ et C₂ peuvent être déterminées en appliquant l’éq. 5) aux résultats des analyses par EF. Il est important de noter que la contrainte de von Mises est ici évaluée à l’aide de la théorie du contact élastique de Hertz, représentant la solution de contrainte dans l’hypothèse d’une élasticité linéaire. La fig. 2b représente les contraintes résiduelles de traction en fonction de la contrainte de von Mises équivalente, à une profondeur de h_c par rapport à la surface, pour le contact linéaire et le contact ponctuel, respectivement. La contrainte critique, S_c, peut être évaluée dans le cadre de la mécanique des ruptures et selon l’approche d’El Haddad [8] pour tenir compte des effets de petites fissures, comme présenté dans nos travaux antérieurs [5].

Expérience et modélisation

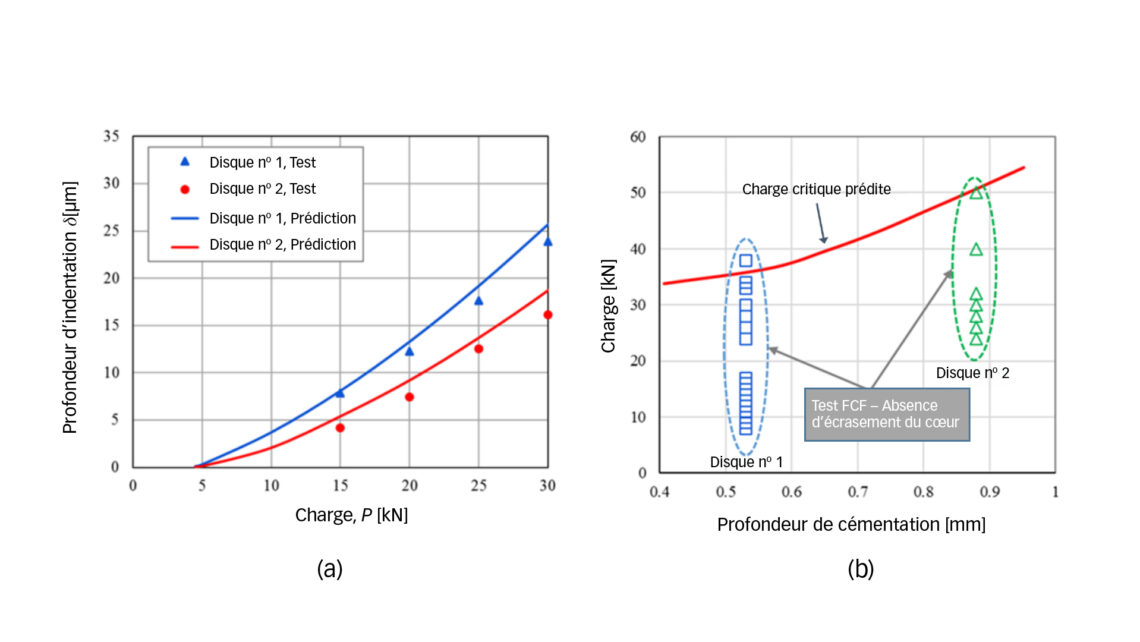
Des tests FCF ont été réalisés sur un échantillon plat en A534-18NiCrMo14-6 selon l’ASTM. Deux disques ont été soumis à une carburation suivie d’une trempe pour obtenir deux profils de dureté avec des profondeurs de trempe de 0,5 mm et 0,9 mm, respectivement. Le matériel utilisé comprenait un pénétrateur de type rouleau bombé de 10 mm de diamètre et 98 mm de rayon de courbure, en acier martensitique ASTM A295-52100. Des jauges de contrainte étaient fixées sur le pourtour de la zone indentée afin de surveiller les variations de contrainte pendant les tests. Il a été établi [4] qu’une augmentation soudaine de la contrainte indique l’apparition d’une fissure latérale dans la zone de transition surface durcie-cœur constituant une preuve de défaillance par écrasement du cœur dans des conditions de charge FCF pour un composant durci en surface.

La fig. 3a présente les indentations plastiques mesurées par rapport aux prédictions des modèles basées sur les éq. 1) – 4). On peut observer une bonne concordance entre les prédictions et les résultats de l’expérience.

Dans tous les tests réalisés sur les deux disques sous différentes charges, aucune indication d’apparition de fissure sous la surface n’a été observée à partir des signaux des jauges de contrainte. L’investigation métallographique post-test a confirmé l’absence de fissure latérale dans les régions sous la surface des disques testés. La fig. 3b présente tous les tests FCF relatifs au disque nº 1 et au disque nº 2, correspondant à deux profondeurs de trempe. La charge critique pour l’écrasement du cœur, correspondant à l’apparition d’une fissure latérale sous la surface, a été calculée et tracée sur la fig. 3b. La prédiction par modélisation est considérée comme plausible, car presque tous les points de données expérimentales, indiquant l’absence d’écrasement du cœur, sont en dessous des charges critiques prédites. Le seul point de données légèrement plus élevé que la charge critique prédite atteste une prédiction prudente du modèle. À noter, les tests FCF effectués sur les deux disques ont impliqué des charges extrêmement élevées en matière de pression de contact nominale. Ainsi, la charge la plus élevée sur le disque nº 1 correspond à une pression hertzienne de 7,1 GPa, tandis que la pression de contact maximale pour le disque nº 2 s’est élevée à 7,7 GPa. Par rapport aux composants durcis en surface par induction [5], l’acier carburé semble, dans cette étude, moins sujet à l’écrasement du cœur, ce qui peut s’expliquer par ses propriétés.

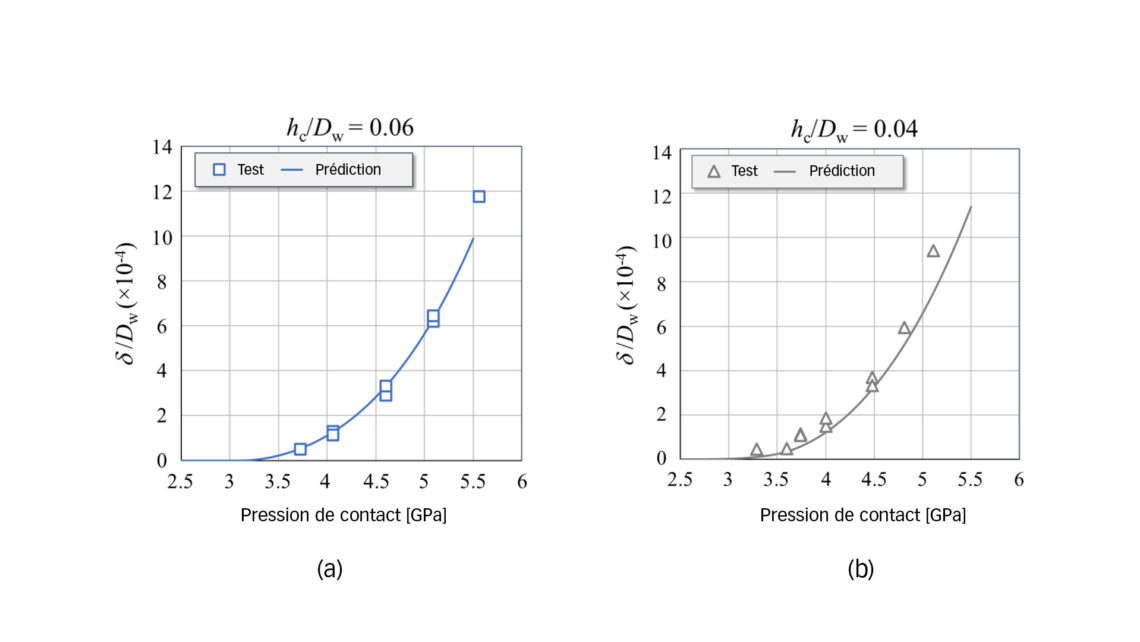
Des tests d’indentation statique ont également été effectués sur la surface du chemin de roulement d’un roulement à rouleaux cylindriques (CRB). L’échantillon testé était un segment de bague intérieure du CRB en acier ASTM A534-18NiCrMo14-6 carburé et trempé. Des rouleaux cylindriques trempés à cœur de différents diamètres ont été utilisés comme pénétrateurs pour créer des conditions de charge avec différentes profondeurs de cémentation en ce qui concerne le rapport h_c / D_w.

La fig. 4 montre les indentations plastiques pour deux profondeurs de cémentation relatives, telles que mesurées et prédites à partir des équations 1) – 4), respectivement. On observe une assez bonne concordance entre l’expérience et la prédiction par modélisation.

Remarques de conclusion

En conclusion, cette étude s’est intéressée à la réponse du matériau de bagues carburées dans des conditions de charge FCF en utilisant une combinaison de simulations numériques et d’investigations expérimentales. Centrés sur l’indentation plastique de la surface et sur l’écrasement du cœur sous la surface, nos modèles établis à partir d’éléments finis ont prédit avec précision l’endommagement du matériau et le comportement de déformation. La validation par des tests FCF réalisés sur un bloc carburé et sur une bague intérieure de roulement à rouleaux cylindriques a confirmé la fiabilité du modèle. Ces travaux permettent non seulement de mieux comprendre les performances des roulements en acier carburé dans des conditions de contact fixe, mais offrent en outre une méthode pratique pour leur évaluation, avec comme implications potentielles l’optimisation de la conception et de la durabilité dans les applications d’ingénierie.