由于许多未知因素，例如制冷剂对润滑剂的稀释、轴承温度、制冷剂压力粘度、粘度随压力和温度的变化、制冷剂在轴承滚道上的化学效应等，制冷压缩机滚动轴承的润滑性能评估一直是一大难题。 在滚动轴承中，使用的润滑性能参数为κ。然而，即使在应用中已知油与制冷剂混合物的有效粘度，也不能应用 ISO 281:2007 [文献1] 中介绍的计算轴承润滑性能参数κ 的经典方法，因为该方法中轴承润滑膜厚度是假设按照纯油计算的，没有考虑制冷剂的存在会降低混合物中压力粘度并增加其可压缩性。因此，过去有几位研究人员提出对原始模型进行修改。

迈耶斯 [文献2, 3] 对滚动轴承的润滑性能参数κ的计算进行了修改，以考虑润滑油中存在被制冷剂稀释的影响。然后他将此参数应用于滚动轴承的 L₁₀ 寿命估算，但没有提供耐久性测试来验证该方法。他还在内部通讯中介绍了雅各布森的发现—— HCFC-22 制冷剂中氯的减少和 HFC-134a 制冷剂中氯的去除显著增加了滚动轴承润滑的粘度要求。迈耶斯估计，对于由 HCFC-22 和矿物油的混合物润滑的轴承，其所需的工作粘度是矿物油润滑的轴承的2倍；对于由HFC-134a 与聚酯 (POE) 油混合润滑的轴承，其所需的工作粘度是矿物油润滑的轴承的3倍。为此，首次在轴承所需粘度的计算中引入了考虑制冷剂化学效应的“工程”安全系数，而不再仅限于油膜厚度的简单计算。这一模型在迈耶斯发表的文章[文献2]进行了总结。

虽然 L₁₀的估算在此应用中仍然是一大挑战，但它可能是明确地将表面与次表面分开计算的理想的轴承寿命模型，如 Morales-Espejel 等人所述 [文献4]。然而，[文献4] 中建议的方法需要正确估计接触面上的油膜厚度，但这一方法的前提是能够正确估计混合物的粘度、压力粘度和可压缩性。 一些研究人员已尝试为此开发新的方法。 尽管取得了进展，但目前很少有文献使用工程方法来估算油与制冷剂混合物的粘度、压力粘度、油膜厚度和所需粘度。 本文介绍了一种通过独立应用粘度随油与制冷剂的压力和温度变化来实现这一目标的方法。然后使用修正后的混合物定律公式来计算混合物的润滑性能。 由此，可以重现丹尼尔图，并且可以估计轴承所需的粘度和润滑性能参数。

混合物定律

文献模型

过去曾进行过研究，来测量和估计由油与制冷剂混合物润滑的弹性流体动压接触处的油膜厚度。 在计算这种油膜厚度时，混合物特性的估计是关键的中间步骤。人们提出了各种不同的公式来估算油与制冷剂混合物的粘度和压力粘度。例如，Akei 和 Mizuhara [文献5] 使用艾林理论推导出计算压力粘度系数与粘度的公式：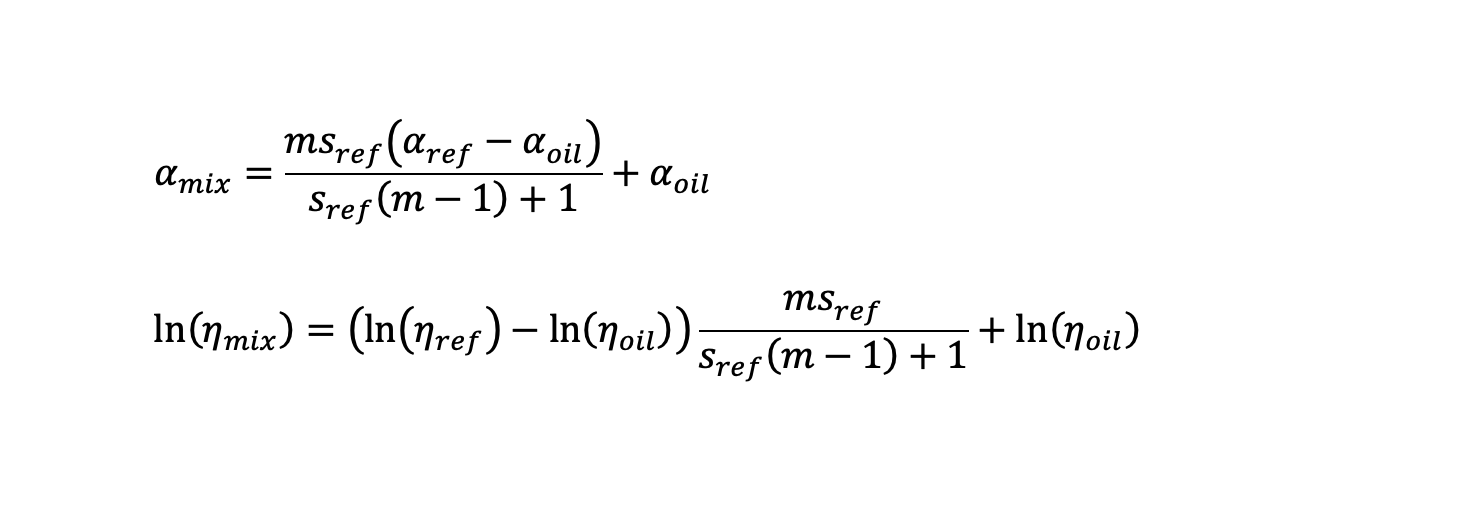

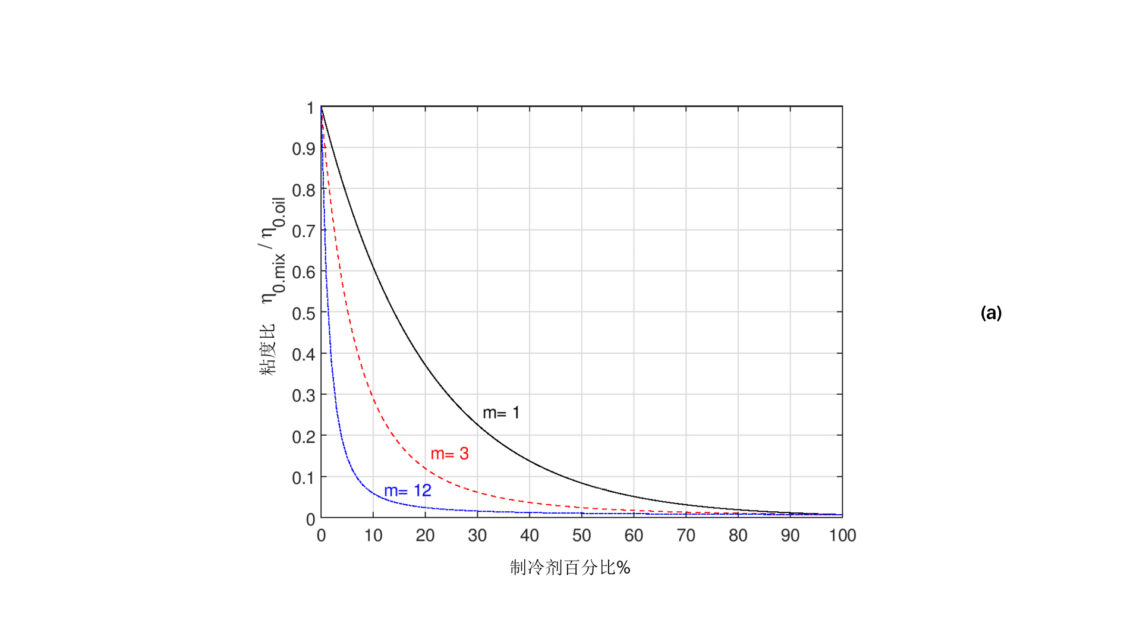
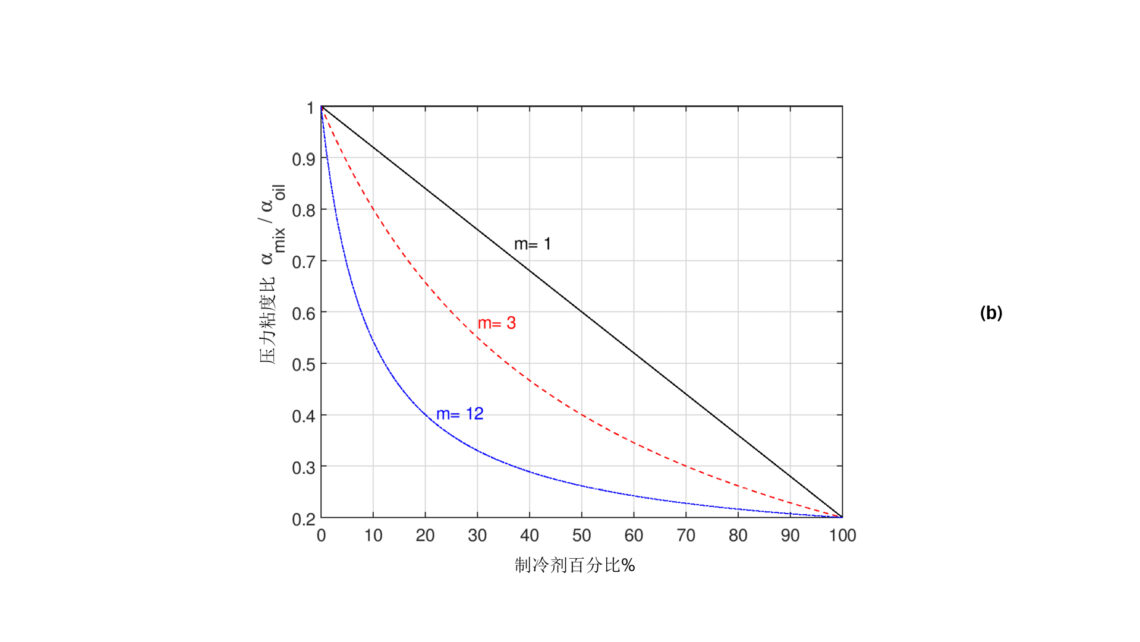
其中m=M_oil / M_ref ，M是成分的分子量。这里α指压力粘度系数，η指动力粘度，s 指成分稀释的百分比，oil指油，ref指制冷剂。可以用上述公式对不同的制冷剂百分比和分子量比绘制图表，如图1所示。

在 Morales-Espejel 和 Hauleitner发表的文章 [文献6] 中，这些公式的预测数值，受到不同的油与制冷剂混合物的实验数据的挑战。使用上述公式和从文献获取的分子量比得到的预测值和测量值之间的不一致，促使人们不断修改公式以更好地预测测量值。

改进模型

用两个函数(k_al, k_et) 乘以分子量比以修改原混合物公式，如下：

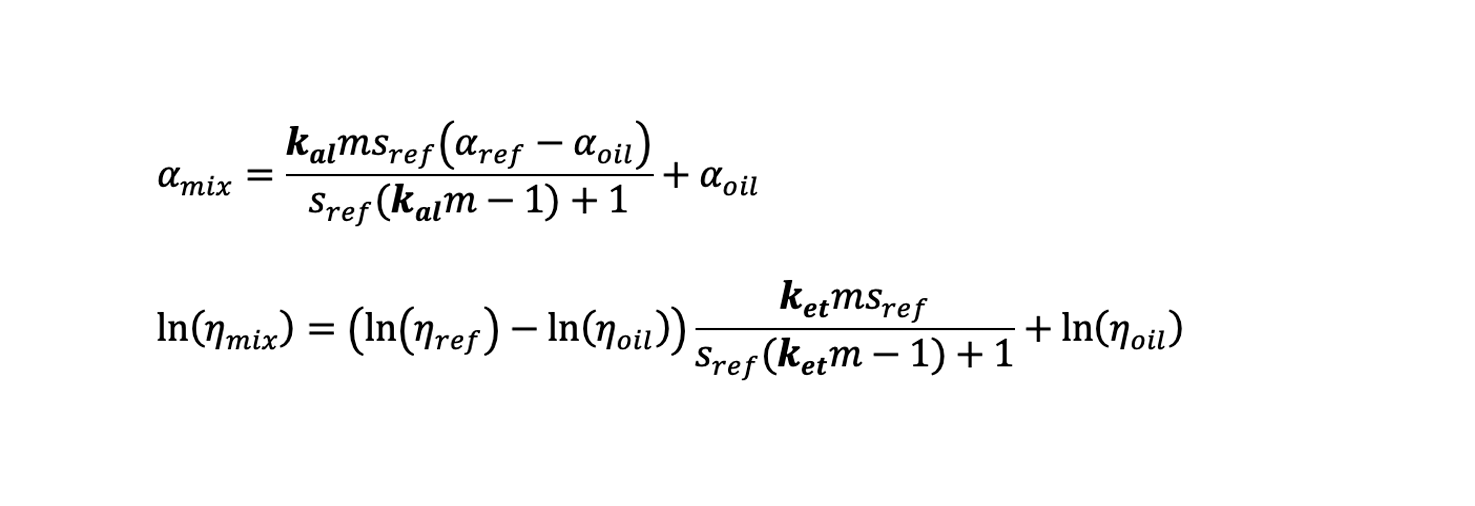
使用不同油与制冷剂混合物的粘度测量值对这些函数进行了校准，因此这些函数取决于油粘度和工作温度。 由此可得：

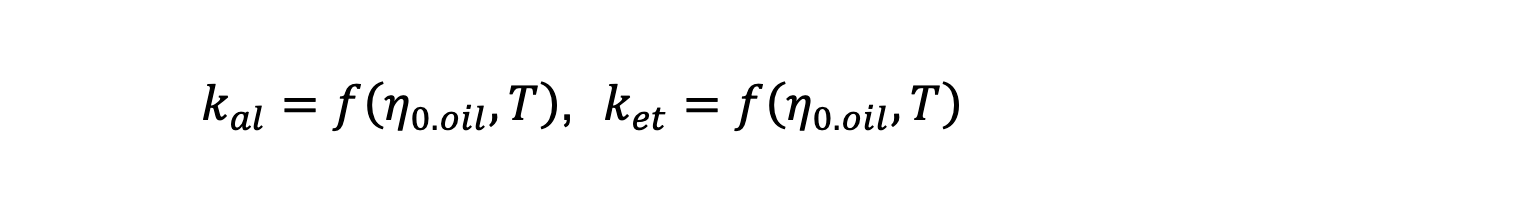
其中，η₀ 是常压下油的动力粘度，T 是温度。

[文献6]中表明，使用改进的混合物粘度模型，获得的预测结果与制冷剂 HFC-134a与聚酯油 100混合物的测量值具有更好的一致性。在不同温度和稀释度下使用其他几种油与制冷剂组合对该模型进行了测试，结果表明该模型预测值与测量结果的一致性总是比原始模型好得多。

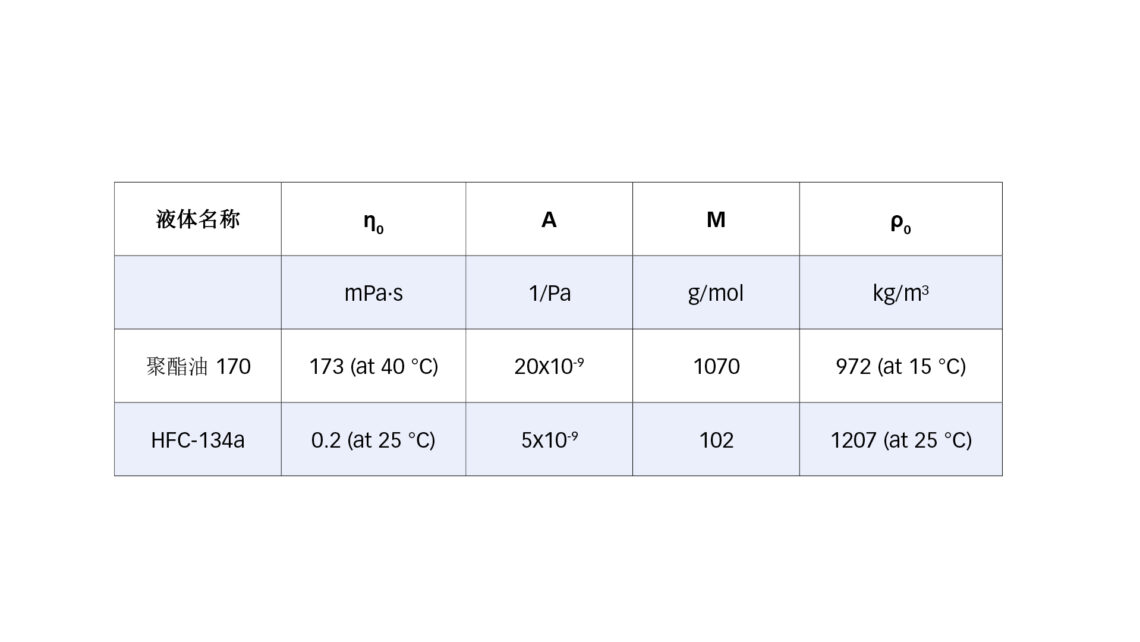
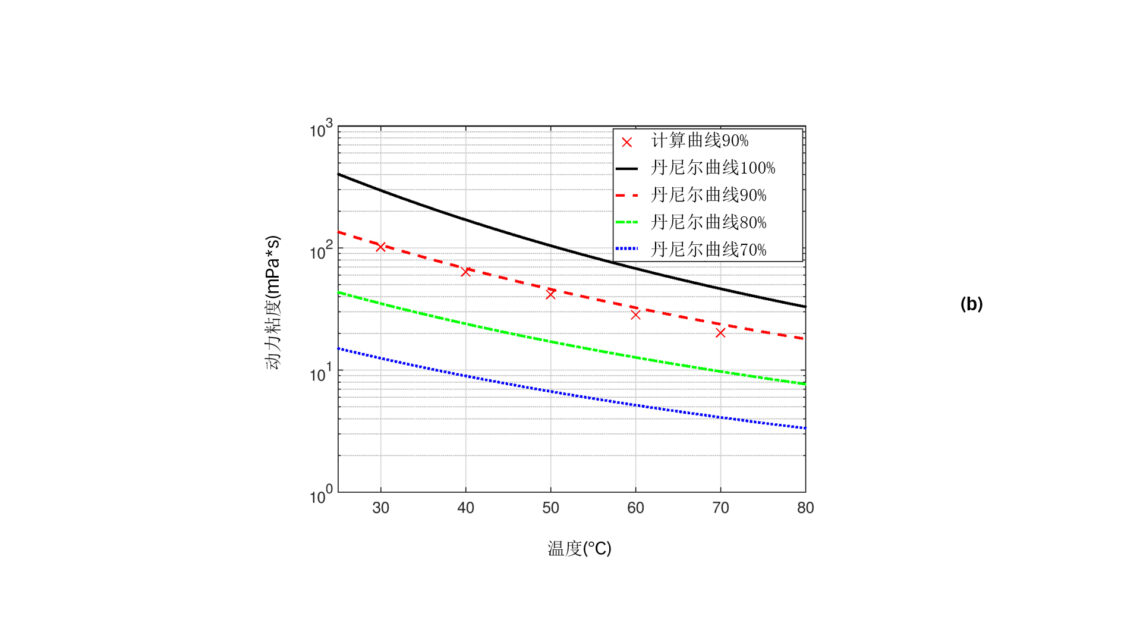
在这项研究中，将所介绍的方法运用于制冷剂 HFC-134a 与聚酯油 170的混合物，这是一种在制冷螺杆压缩机采用福斯油品公司[文献7]润滑油的典型组合。所考虑的液体特性汇总在表 1 中。该混合物的丹尼尔图如图 2 所示，并发表在福斯油品公司的手册中 [文献8]。

按照上述方法，可以根据各种流体的特性再现丹尼尔图曲线。在本示例中，表 1 中的数据用于重现聚酯油 170与10%的HFC-134a制冷剂的粘度。图 3 显示了计算数据与丹尼尔图数据之间的良好一致性。

滚动轴承的润滑性能

对于由油与制冷剂混合物润滑的滚动轴承的润滑性能参数κ，[文献6]中提出了修正。将油与制冷剂混合物最终调整后的实际粘度代入kappa值计算公式(κ=ν_adj ⁄ ν₁ )，其中调整后粘度为：

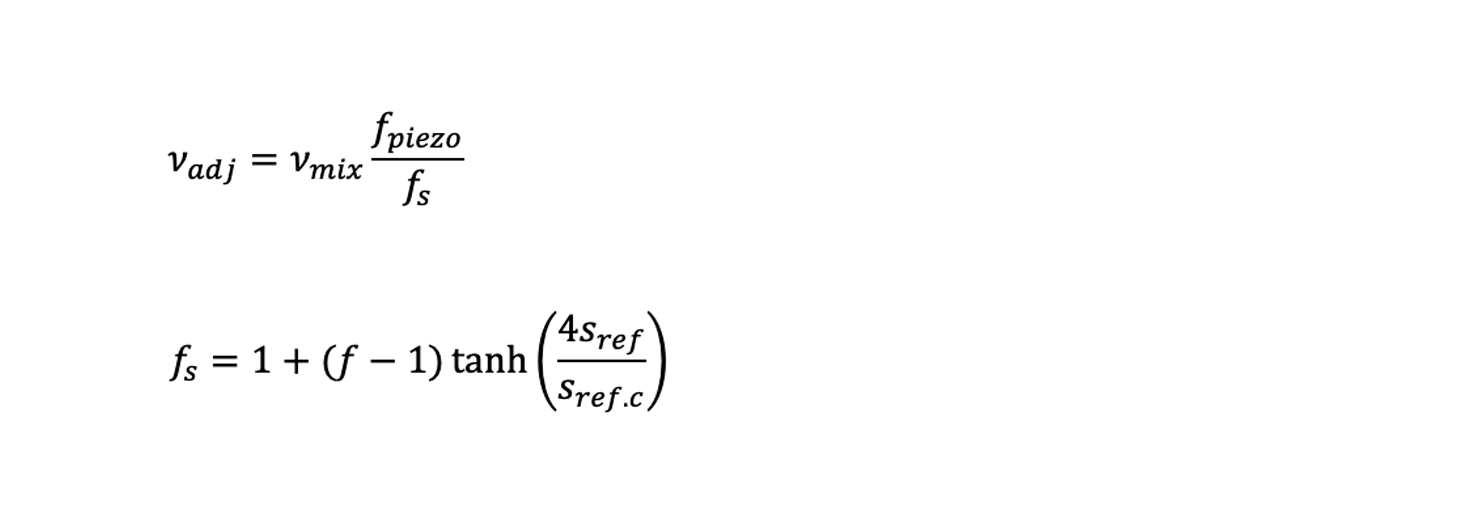
和，

 

 

请注意，从数学上讲，调整系数 f_{adj =} f_piezo / f_s 没有上限，可以达到 100% 制冷剂的混合率。然而，全钢制轴承当然无法承受这种工况，如 [文献10] 中所述。 因此，出于实际原因和技术上的弥补，建议将制冷剂最大稀释率限制为30% (s_ref <0.3)。

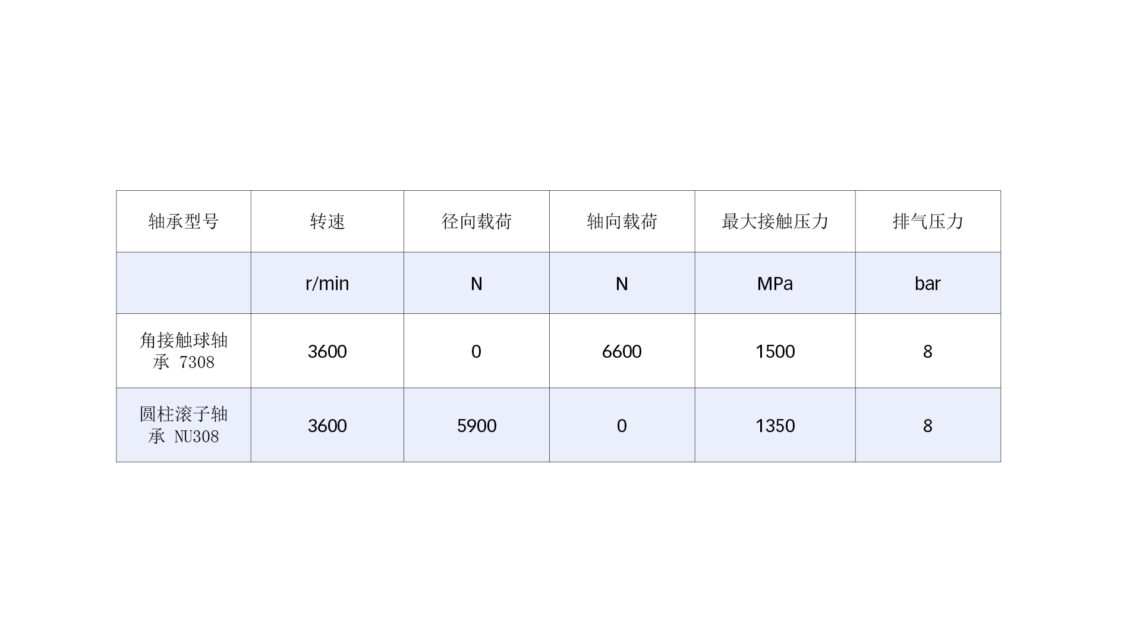
在下文中，我们将考虑一个实际应用示例，并展示所描述方法的潜在可能性，以及润滑剂粘度特性对系统计算的影响，同时分析空调系统中螺杆压缩机轴承的润滑性能。运行条件汇总在表 2。

虽然前面的部分中，仅研究了液体特性与某一输入变量之间的关系，例如，混合物粘度与图1的稀释度或图 2 (b) 的温度的关系。但我们想举例说明现实中多个参数对轴承润滑性能的综合影响。为此，我们假设输入参数之间存在某些关系，如下所述。

温度和稀释的影响

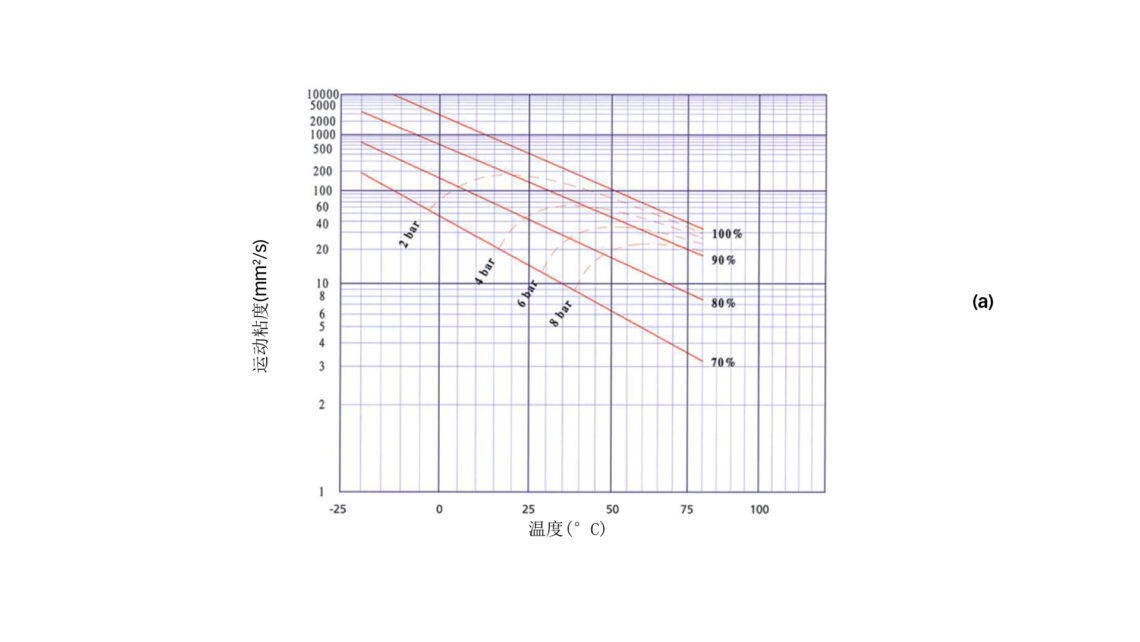
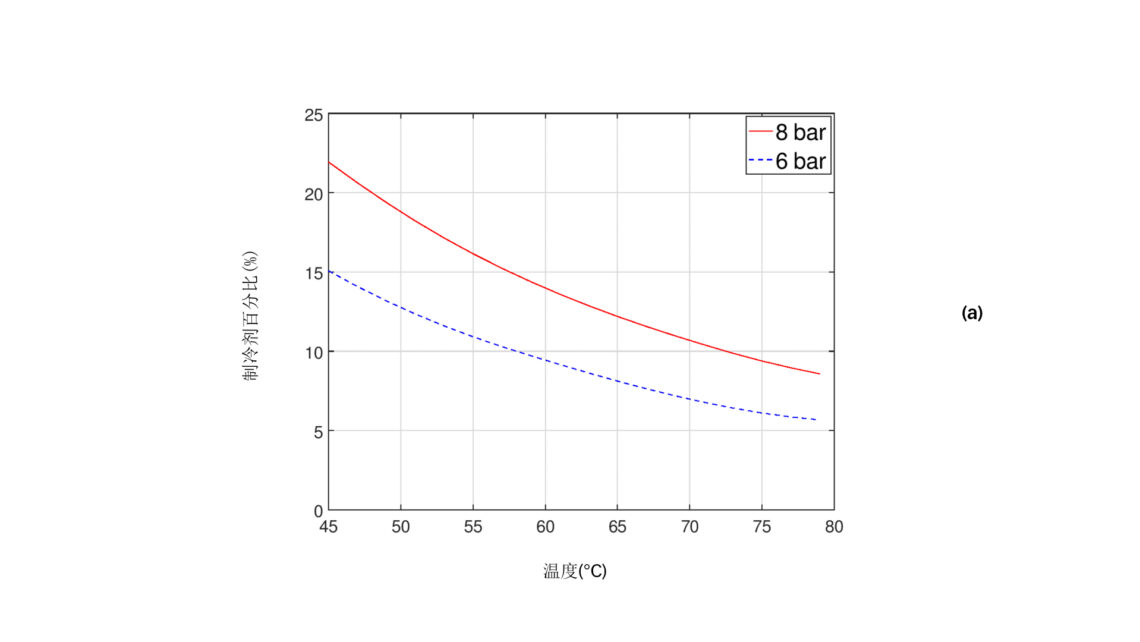
稀释特性与压力和温度之间的关系对于每种油与制冷剂混合物都是特定的，这些信息包含在丹尼尔图中。在这个例子中，我们假设润滑条件由压缩机的排气压力决定，由此产生的油与制冷剂混合比在丹尼尔图中由压力线（等压线）和温度线的交点所确定。在图 3 (a)中，两个压力信息是从图 2 (a)中给出的丹尼尔图中获取的。对于聚酯油170与HFC-134a的混合物，在6巴和8巴时，制冷剂对油的稀释随温度升高而降低。在实测的温度范围内和 8 巴时，混合物中含有8%到22%的制冷剂。

在给定压力和温度下的稀释度是影响轴承润滑性能的重要因素，它取决于油与制冷剂的实际混合比例。与 HFC-134a等上一代制冷剂相比，具有低温室效应潜能值 (GWP) 和零臭氧消耗潜能值 (ODP) 的制冷剂通常会导致更高的稀释度。

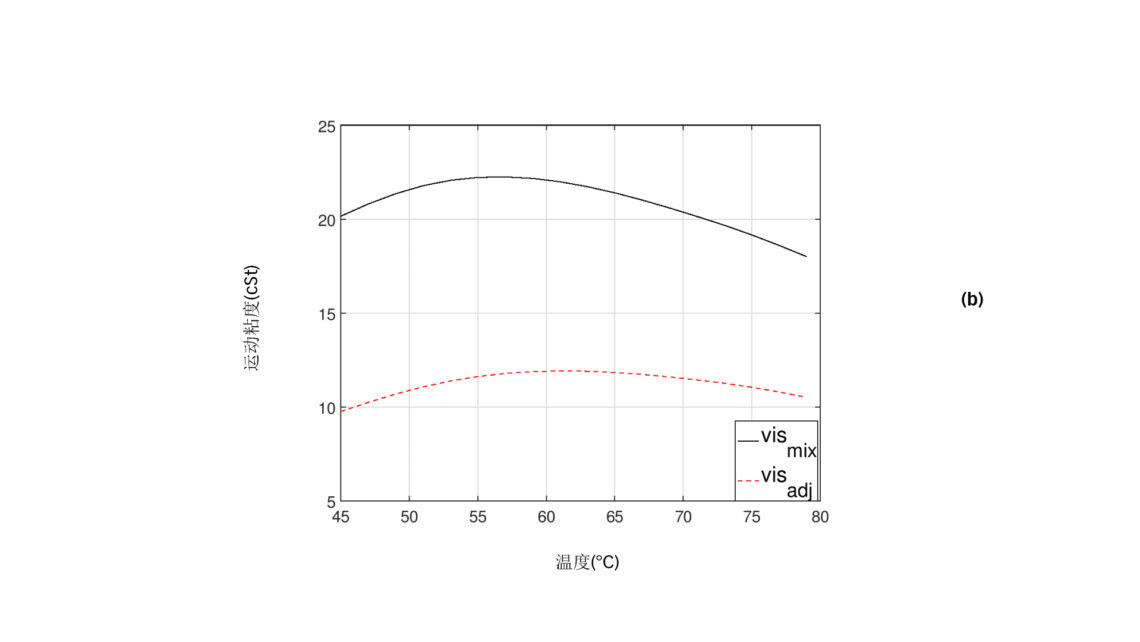
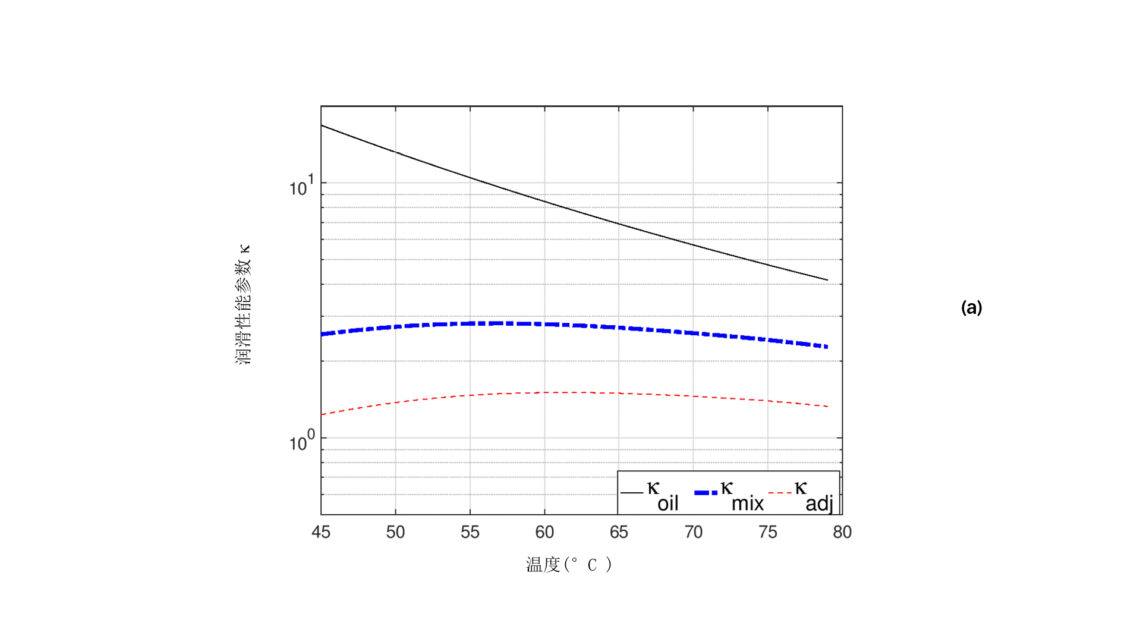
由于混合物粘度以及压力粘度随着稀释度的增加而下降（见图 1），并且粘度随着温度的升高而降低（见图 2(a)），按照图3 (a)中稀释度和温度的特征，将导致这两种相反趋势的叠加。这形成了一个有趣的特性，在所研究的温度范围内形成一个最大的粘度值，并且粘度随着温度的降低或升高而下降。这种效应也出现在丹尼尔图的等压线上。图 3 (b) 显示了根据修正后的粘度混合公式和调整后的混合物粘度v_mix 再现8 巴下的混合物粘度v_adj ，包括压力粘度效应和建议的安全系数导致的粘度降低。在整个示例中，使用了设定为1.5 的雅各布森安全系数 f。

由于角接触球轴承 (ACBB) 和圆柱滚子轴承 (CRB) 在所选运行条件下的润滑性能参数结果非常相似，因此下图仅代表角接触球轴承的结果。

在表2中的轴承运行条件下，根据调整后粘度的公式计算润滑性能参数。图4 (a)中结果表明，从纯油到混合物，润滑性能显著降低，并且所描述的附加效应（压力粘度、安全系数）导致 kappa值进一步严重降低（图表以对数刻度绘制）。调整后的kappa值大约是使用混合物粘度（由常见的丹尼尔图给出）获得的kappa值的二分之一。对于纯油润滑，较高的温度会导致kappa值降低，而油与制冷剂混合物的特性表明在实测温度范围的较低区域和较高区域内，对润滑条件具有挑战性。在温度坐标的低温区，随着温度的升高，稀释度减少的影响（图 3 (a)）占主导地位，因此kappa值增加。在高温区，温度的升高会降低含油较多的混合物的粘度，因此kappa值会降低。

排气压力的影响

接下来我们重复相同的评估，但假设排气压力为 6 巴而不是 8 巴（保持与之前相同的转速）。图3 (a)显示了由于压力下降而导致的稀释度减少。在实测的温度范围内，制冷剂含量在6巴时介于6%和15%之间。

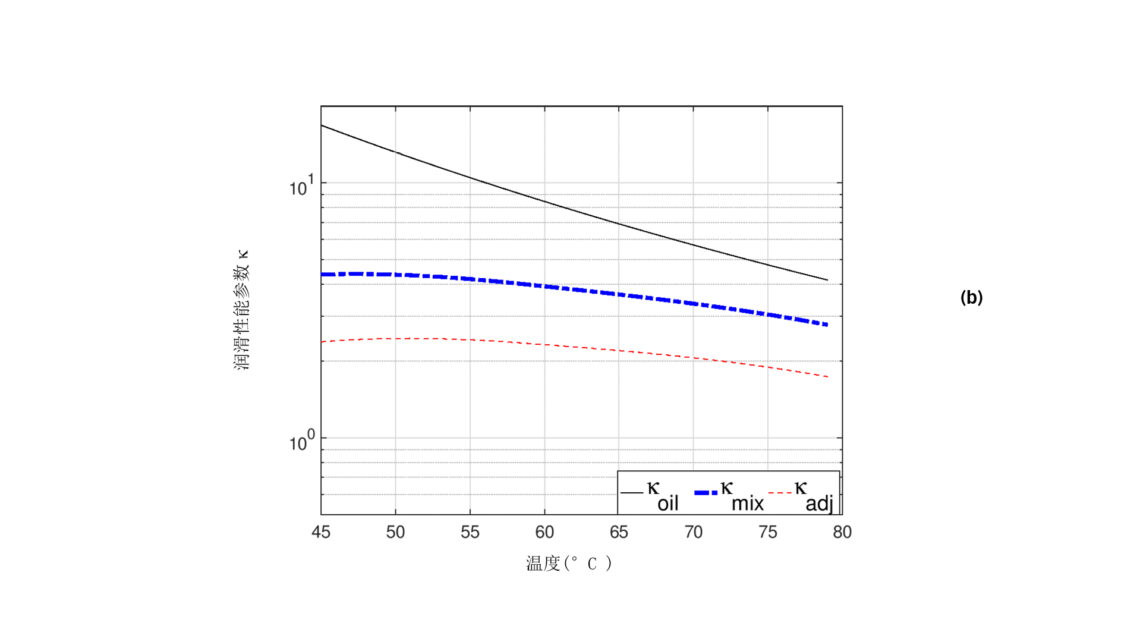
图4 (b)显示了6巴条件下的润滑性能。如丹尼尔图所示，压力下降导致相同温度下的稀释度降低，因此与8巴的情况相比，混合物粘度和kappa值都增加了。

转速的影响

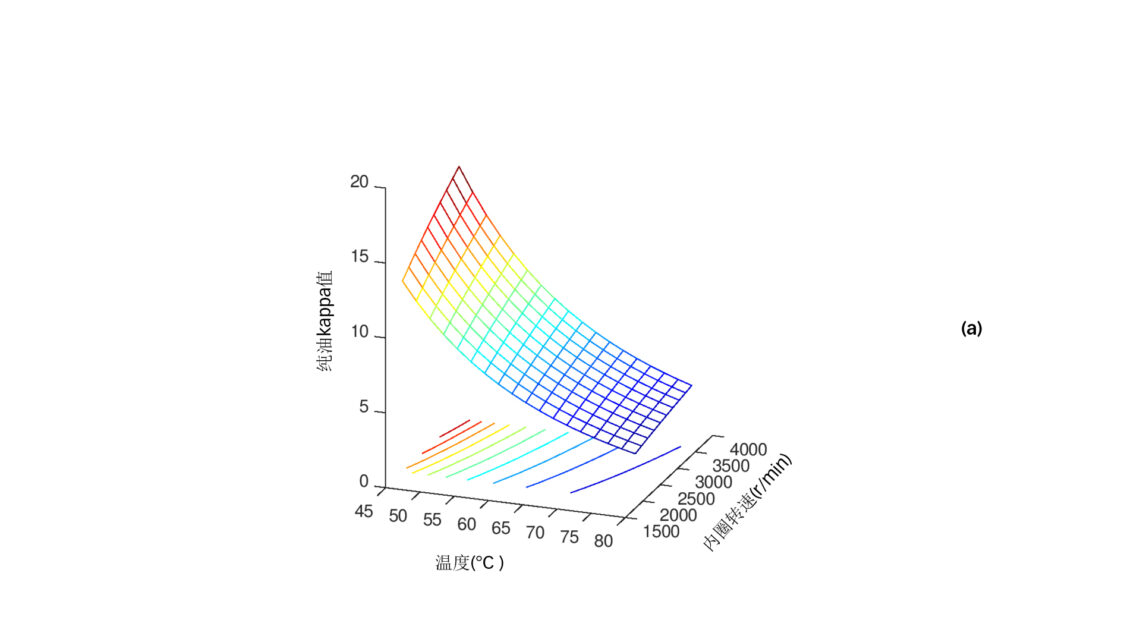
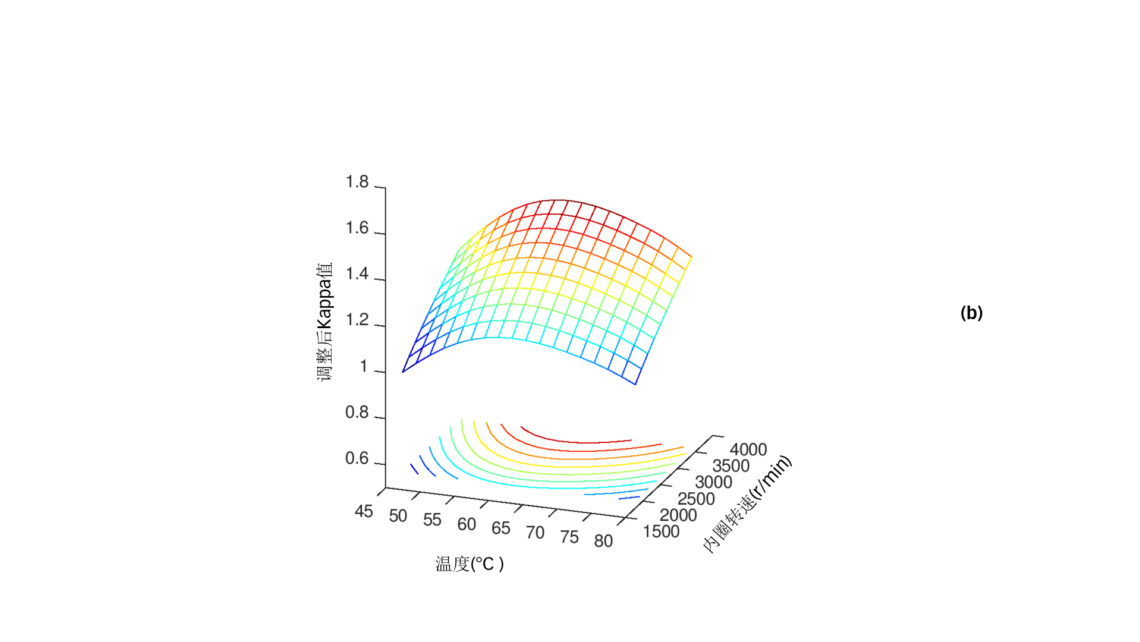
随着变速驱动器 (VSD) 的引入，运行范围的另一个因次是压缩机转速。转速是滚动轴承中油膜厚度的一个重要参数。我们继续使用之前的条件，并用新增的转速因次来绘制数据。

图5比较了纯油（尽管在给定条件下具有高得离谱的粘度）和油与制冷剂混合物的润滑性能参数特性。对于纯油的工况，润滑性能最差的区域位于高温和低速。对于油与制冷剂混合物的工况，则显示出明显较低的kappa值和不同的特性。两个润滑性能最差的区域都在低速范围内，一个在实测范围的低温区域，另一个在高温区域。这解释了为什么在大多数情况下，双螺杆压缩机轴承润滑性能的关键位置在阴转子（转速较慢的转子）。最终，降低转速的效果应该与降低排气压力的效果叠加。

结论

本文介绍了一种用于估算滚动轴承润滑性能参数κ的完整方法。首先，提出了精确的粘度和压力粘度混合物定律公式。使用这些公式，可以推导出其他方法无法获得的相应丹尼尔图。然后用这些公式估算混合物的粘度。该方法推导出了当存在油与制冷剂的混合物时轴承中实际粘度的调整系数。将该调整系数与用润滑油计算法得出的混合粘度相乘，就会将粘度值降低到安全水平。

如本研究所示，雅各布森安全系数f为工程师提供了一定的自由度，能调整设计的安全性，因为仍然存在一些未知的影响因素。其中之一已经在 [文献10] 中讨论过，就是制冷剂对轴承钢的化学侵蚀性，由于腐蚀或润滑性能差而降低其疲劳强度。例如，有极低温室效应潜能值 (GWP) 和零臭氧消耗潜能值 (ODP) 的制冷剂可以被认为是高活性和腐蚀性液体，尤其是在存在水分的条件下。在这种情况下，鼓励工程师使用 f≥2，其它情况用1.5≤f≤2就足够了。

对于实际应用，所有影响混合物润滑性能的参数，例如温度、压力、转速，都将与空调机组的运行周期相关。按照建议的方法，可以预测运行图中每个点的轴承润滑性能。

通过这一分析，可以得出以下结论：

1. 文献中给出的油与制冷剂混合物定律公式需要一些依赖于润滑油粘度和温度对应的函数关系才能准确预测混合物粘度和压力粘度。
2. 利用滚动轴承中的润滑油计算法得出的混合物粘度仍需要调整压力粘度和安全系数，才能用于计算在油与制冷剂混合条件下运行的轴承润滑性能。
3. 雅各布森安全系数是应用设计的相应变量。高活性制冷剂（尤其是水分存在的情况下）将需要更大的安全系数值