影响轴承性能的最佳渗碳层深度

为了增强轴承的耐磨性和承载能力，其工作接触表面会采用特定工艺进行热处理。由于轴承尺寸和所用钢材品种等相关因素存在差异，部件可能要进行淬透处理或表面淬硬处理。高碳钢适用淬透处理工艺，而低碳钢（碳含量低于 0.25%）则适用表面硬化处理，可以通过渗碳等工艺来实现。对于中碳钢而言，表面感应淬火是另一种广泛应用的处理方法。

渗碳就是在高温环境下将碳原子渗入到低碳钢中，从而在淬火时形成被称为“表层”的硬化层。表面硬化轴承的承载能力取决于硬化表层深度和芯部强度等多个因素。因此，轴承制造商在制造过程中必须谨慎选择钢材，并确保针对特定的应用要求，渗碳层有足够的深度。然而，过大的硬化表层深度不仅会增加不必要的制造成本，还可能在硬化过程中导致裂纹的产生，并引发如晶间氧化和晶粒变大等不良后果[文献1]。

芯部挤压[文献2, 3]是表面硬化轴承的一种失效模式，是由于硬化表层深度不足、接触负荷过大而引起的。这种失效表现为在硬化层下芯部材料内裂纹的萌生，并随之不断地扩展。由于滚动接触产生的应力可能超过芯部的静强度或疲劳强度，表层和芯部之间的硬度差异对芯部挤压有重大影响。阿尔弗雷德松和奥尔森[文献4]以及拉伊等人[文献5]在研究过程中观察到，在承受持续接触疲劳负荷条件下，表面硬化试件中会出现芯部挤压情况。持续接触疲劳试验是一种使用滚珠或滚子对试件表面进行循环压痕的测试。数值模拟[文献5]表明，当表层深度较浅或接触负荷过大时，表层和芯部之间的过渡区会产生明显的残余拉伸应力，进而在持续接触疲劳负荷下形成横向裂纹。芯部的严重塑性变形削弱了其对渗碳层的支撑。一旦应力超过极限，就可能导致表层弯曲并形成裂纹。除了芯部挤压外，表面硬化轴承的静态承载能力还表现为静态接触负荷下的塑性变形。然而，ISO 76 [文献6]中定义的额定静态载荷并未考虑表面硬化轴承。为了评估表面感应淬火回转支撑轴承滚道的塑性压痕，已经有人提出了计算方法[文献5]。

本文根据我们最近发表的一项研究[文献7]，旨在对持续接触疲劳条件下表面渗碳轴承的材料特性进行表征和建模。通过评估表面塑性压痕和芯部挤压的风险，为设计工程师和制造商提供了深度见解，尤其是优化表面渗碳轴承性能方面的见解。

数值模拟和建模

我们使用ABAQUS商业软件进行有限元分析，模拟表面渗碳轴承套圈中滚动体与滚道表面之间的相互作用。模拟涵盖了三种接触类型：点接触、线接触和椭圆接触。

我们的研究重点是了解材料对持续接触负荷的响应，因此材料的弹塑性特性在有限元模型中显得至关重要。描述弹塑性变形涉及应力和应变的关系，通常用拉伸或压缩试验获得。由于材料的强度与硬度密切相关，所以我们将渗碳部件的强度梯度与硬度分布相关联。通过压缩试验，建立了芯部结构和硬化表层结构的应力和应变曲线，我们采用线性插值法来估算出硬度不等的材料的应力和应变关系。

有限元模型为评估由持续接触负荷引起的表面塑性压痕和次表面损伤提供了便利。通过对不同负荷条件和硬度分布的参数研究，我们推导出了滚道塑性变形与渗碳层深度的函数关系、渗碳层和芯部硬度的函数关系、滚动体直径和接触压力的函数关系等经验公式。此外，该研究还确定了在持续接触负荷条件下表面渗碳轴承套圈可承受的次表面损伤极限。

以一个硬度均匀的部件为例。它类似于渗碳前的淬透处理或芯部结构，则其表面塑性压痕（δ）与最大接触压力（p₀）和材料屈服强度（σ_y）的关系为：

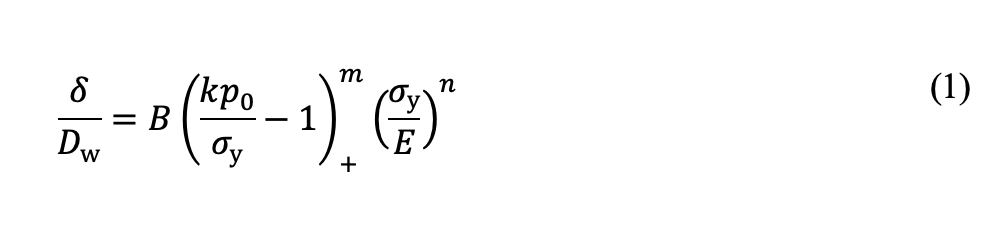
式中，D_w 表示滚动体直径，(…)+表示麦考利括号。当括号内的值为负时，该项取值为0。k为常数，与具体材料无关。它将接触压力p₀和最大冯·米塞斯等效应力σ_vM（σ_vM = kp₀）联系起来。对于点接触，k = 0.62；对于线接触，k = 0.56。常数B、n和m是与材料相关的特定值。

如果该部件经过了表层渗碳和硬化处理，则表层和芯部的变形都会产生塑性压痕。这些因素的影响大小取决于表层相对深度（h_c /D_w）。此时，表层深度h_c被定义为硬度等于HV550处的深度。拉伊等人[文献5]得出的计算公式如下：

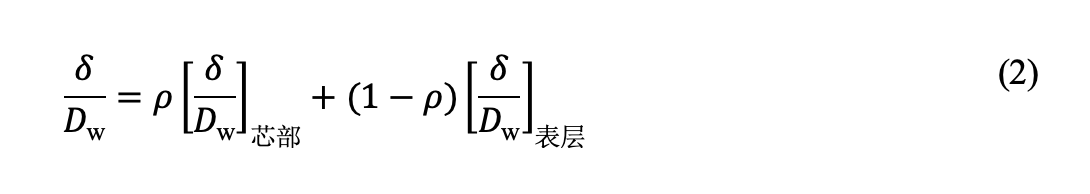
式中，[δ /D_w]_表层和[δ /D_w]_芯部分别代表表层和芯部材料的塑性压痕，由公式（1）计算得出。公式中的分区参数ρ是表层相对深度h_c /D_w与接触压力的函数：

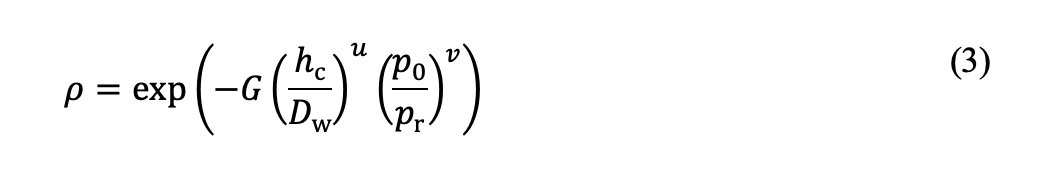
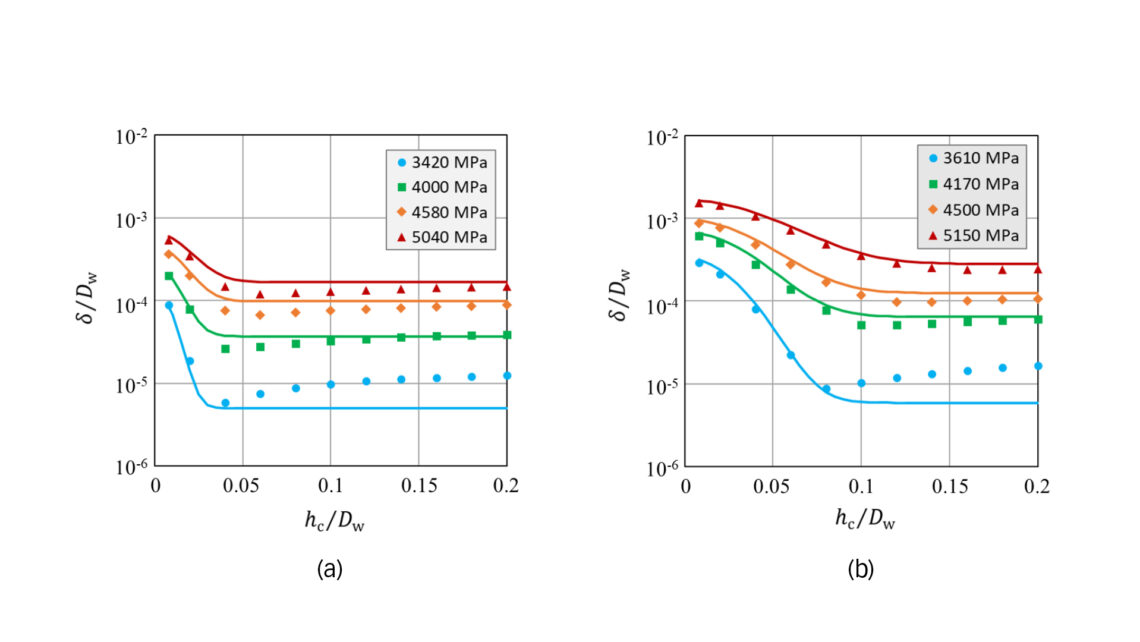
式中，p_r是设定为1000 MPa的参考压力。如图1所示，常数G、u和v是通过将公式（3）与公式（2）拟合到从有限元计算中所得到的塑性压痕数据来确定的。请注意，经淬透处理过的轴承的额定静载荷定义为表面塑性压痕深度为10^-4D_w时相对应的接触压力[文献6]。

椭圆接触塑性压痕[δ /D_w]_EC是根据点接触和线接触解法之间的b /a比率进行插值计算得出的：

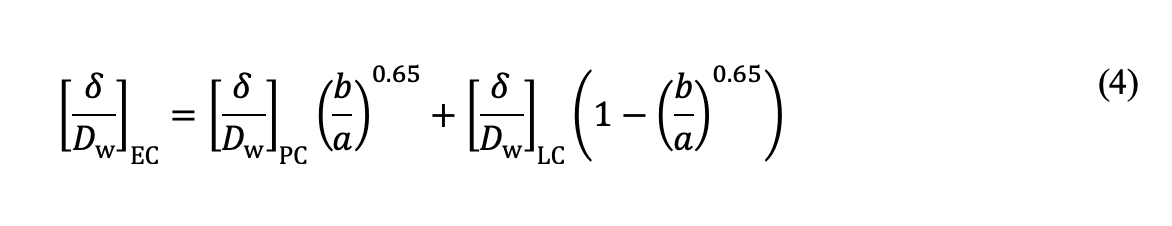
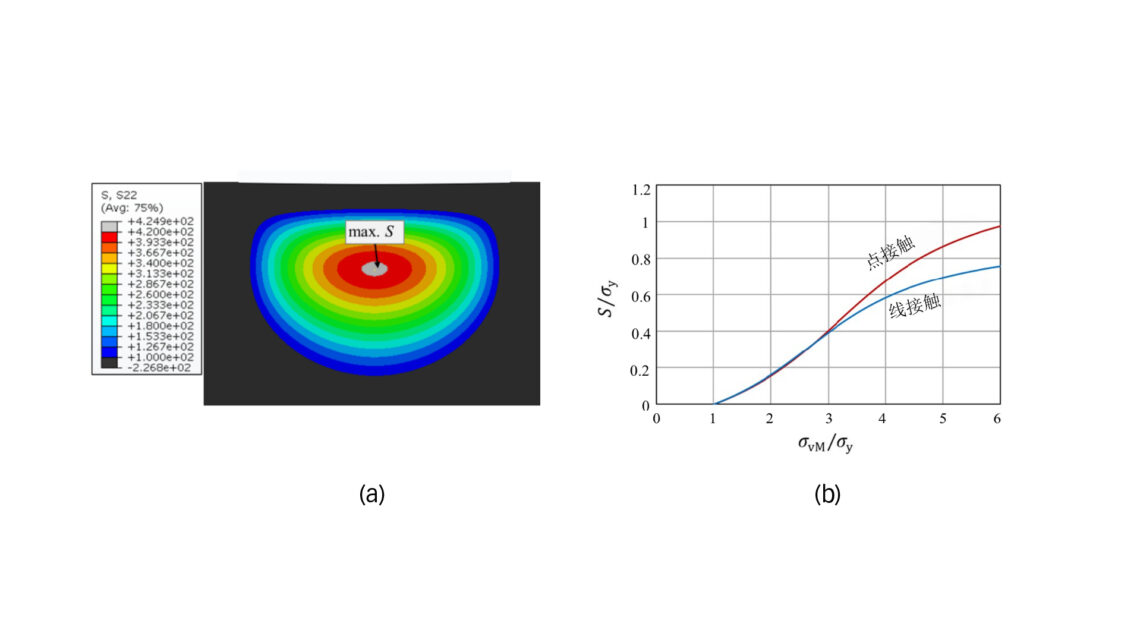
通过有限元分析，我们探讨了材料对塑性变形引起的残余应力的响应。当静载荷产生的应力超过芯部材料的屈服强度时，就会发生塑性流动，进而在材料内部产生以残余应力形式存在的次表面损伤。图2a显示的是在高接触应力下表层与芯部瞬态区域的残余拉伸应力区。如先前的一项研究[文献5]所示，在承受滚珠或滚子压痕的表面感应淬火部件中也发现了类似的残余应力模式。该研究表明，在持续接触疲劳负荷条件下，残余拉伸应力可能会在表层与芯部界面引发开裂或分层。

之前推导出来的持续接触负荷引发的次表面残余拉伸应力公式[5]，已被证明适用于表面渗碳部件：

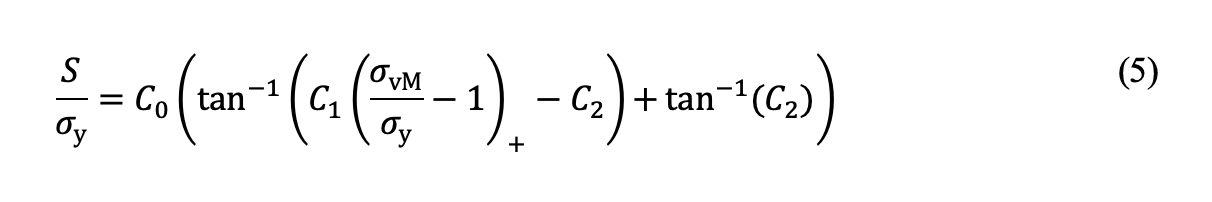
式中，σ_y表示芯部材料的屈服强度，σ_vM 表示距表面的深度h_c 或硬度等于HV550深度处的冯·米塞斯等效应力。C₀、C₁和C₂为常数，可通过将公式（5）与有限元结果拟合来确定。值得注意的是，此处的冯·米塞斯应力是根据赫兹弹性接触理论进行评估的，它代表了线性弹性假设条件下的应力解法。图2b分别显示了线接触和点接触时距表面深度h_c处的残余拉伸应力与冯·米塞斯等效应力的函数关系。临界应力S_c可使用断裂力学原理和埃尔·哈达德[文献8]方法进行估算，以考虑小裂纹效应，具体情况参考我们之前的研究[文献5]。

实验和模型验证

我们在采用ASTM A534-18NiCrMo14-6材料制成的平面试件上进行了持续接触负荷试验。两个圆盘试件经过渗碳硬化后，得到两种硬度分布，其表层深度分别为0.5mm和0.9mm。持续接触负荷试验使用的是直径为10mm、冠状半径为98mm的冠状滚子压头，由马氏体淬硬的ASTM A295-52100钢制成。在压头区域外侧安装了应变仪，用于监测测试过程中的应变变化。此前已有研究[文献4]表明，应变的突然增加表明表层与芯部过渡区开始出现了横向裂纹。这可以作为表面硬化部件在持续接触负荷条件下发生芯部挤压失效的证据。

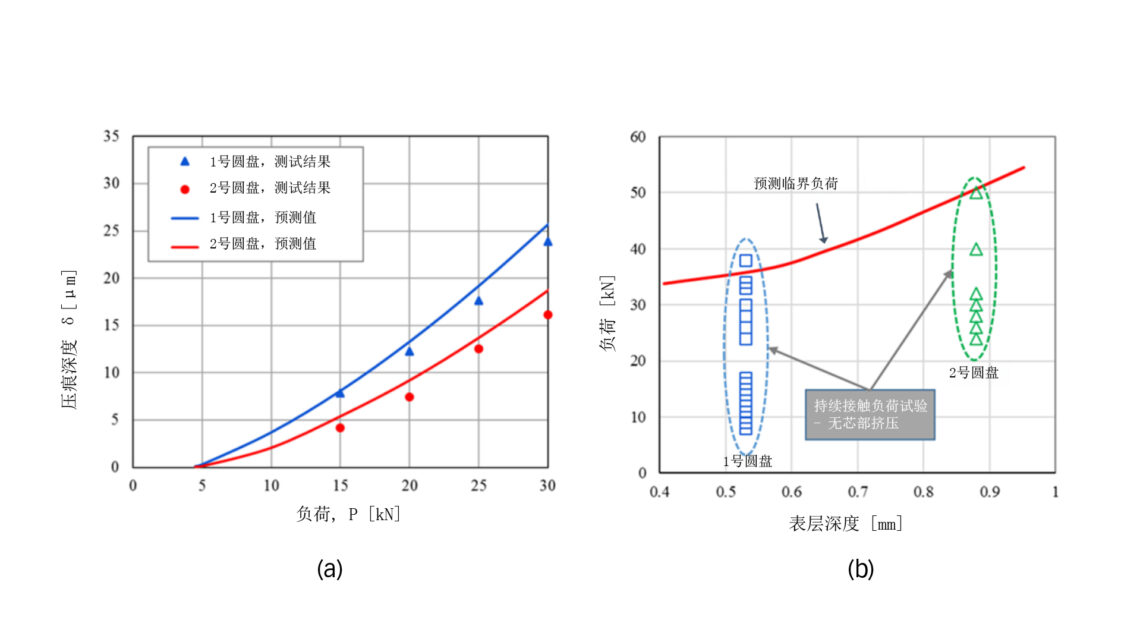
图3a显示了实际测量的塑性压痕与通过公式（1）–（4）得到的模型预测值之间的对比，结果显示，预测值与实验数据之间具有良好的一致性。

对于在不同负荷下对两个圆盘进行的所有测试，均未从应变仪信号中观察到次表面区域出现横向裂纹的迹象。随后的金相分析也进一步确认了受检的圆盘次表面区域也没有出现横向裂纹。图3b显示了按1号圆盘和2号圆盘分组的所有持续接触负荷试验结果，它们分别对应两种不同的表层深度。图中还计算并绘制了表示次表面横向裂纹萌生的芯部挤压临界负荷。模型预测结果被认为是可信的，因为几乎所有表明未发生芯部挤压的实验数据点均低于预测的临界负荷。唯一一个略高于预测临界负荷的数据点表明该模型预测较为保守。值得注意的是，两个圆盘的持续接触负荷试验都涉及极高的公称接触压力。例如，1号圆盘的最高负荷对应的赫兹压力为7.1 GPa，而2号圆盘的最大接触压力则达到了7.7 GPa。与表面感应淬火部件相比[文献5]，本研究中的表面渗碳钢因其特性而更不易受到芯部挤压的影响。

此外，我们还对圆柱滚子轴承的滚道表面进行了静态压痕测试。测试样本是从圆柱滚子轴承内圈上截取的一段，其材质为经过表面渗碳和硬化处理的ASTM A534-18NiCrMo14-6钢。测试中使用了不同直径的淬透圆柱滚子作为压头，以获得不同表层相对深度（h_c/D_w比）的负荷条件。

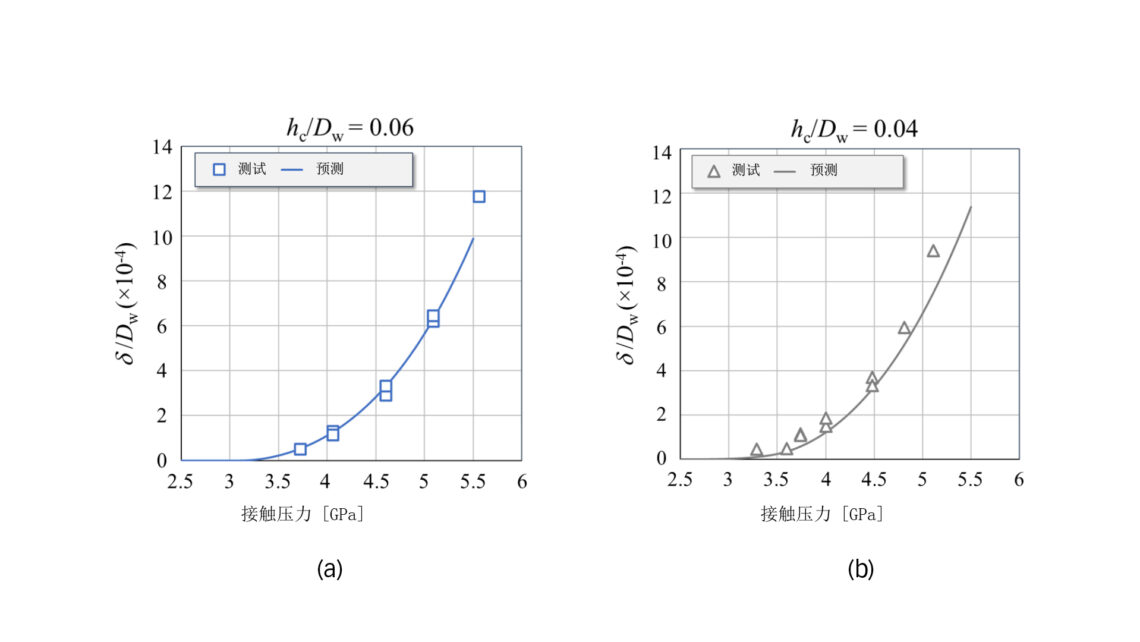
图 4 显示了两种不同表层相对深度下的塑性压痕。这些压痕分别通过实际测量和套用公式（1）–（4）预测得到的。实验结果与模型预测结果具有良好的一致性。

结束语

综上所述，本研究采用数值模拟和实验验证相结合的方法，深入探讨了表面渗碳套圈在持续接触负荷下的材料响应。通过关注表面塑性压痕和次表面芯部挤压现象，根据有限元模型准确预测出材料的损伤和变形特性。通过在渗碳圆盘和圆柱滚子轴承内圈上进行的持续接触负荷试验，验证了该模型的可靠性。此项研究不仅加深了人们的理解，还为评估表面渗碳轴承在持续接触条件下的性能提供了一种实用方法，这对于优化工程应用中的设计和耐用性具有重大的意义。