深入了解材料
缺陷
SKF一直在不断开展研究,以深入了解微观结构和预先存在的材料缺陷对轴承性能的影响。这些研究工作至关重要,有助于明确哪些特征及其严重程度会对轴承性能产生举足轻重的影响。
如今,由于滚动接触疲劳(RCF)而导致的轴承失效通常较为罕见,而且滚动轴承的最终使用寿命通常超过计算额定寿命。然而,在有些情况下,特定应用中的轴承可能会过早失效。轴承性能要获得持续改进,了解轴承失效机理至关重要,这样才能满足现代滚动轴承应用场合对不断提高的功率密度的要求。
用于各种应用场合的滚动轴承的可靠性遵循最弱环节原则,也就是说,失效是有关系统内部最薄弱环节受损造成的。在不良润滑条件下,轴承失效可能是由表面损伤造成,表现为表面疲劳或磨损。此外,最弱的环节可能存在于次表面区域,这是因为赫兹接触产生的剪切应力在滚道表面以下的某一深度处达到最大值。而且,与大多数高强度材料一样,轴承钢一般存在损伤容限较小的问题,表现为对预先存在的材料缺陷(如作为炼钢工艺副产品的非金属夹杂物)较为敏感。
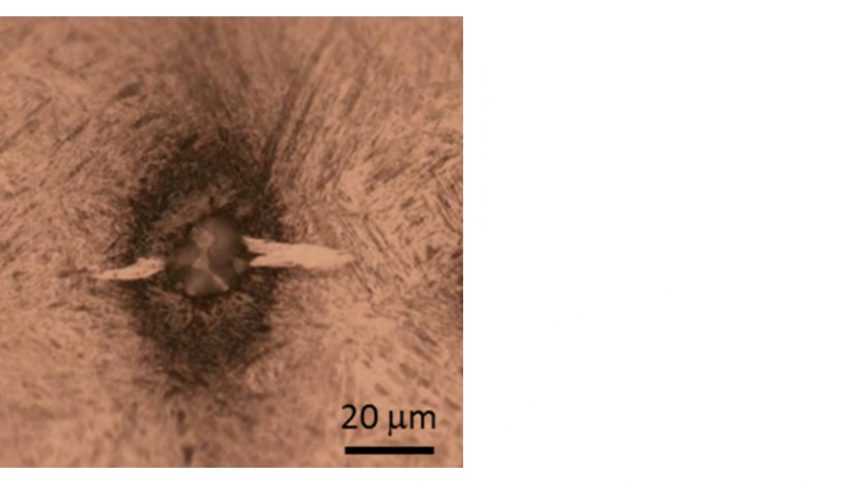
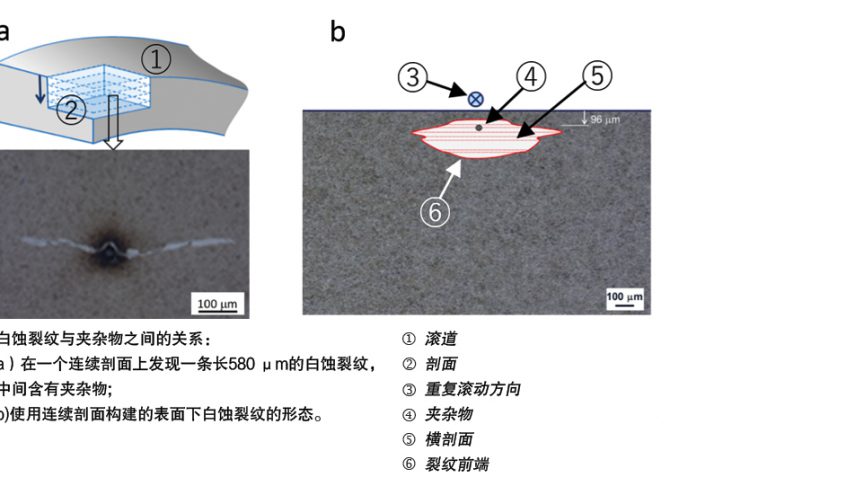
针对滚动接触疲劳测试样品的金相研究表明,所谓的“蝴蝶”通常由非金属夹杂物发展而来。通过光学显微镜从金相腐蚀样品中看到的“蝴蝶”,实际上是两条源自夹杂物的裂纹,它们被白蚀区所点缀(如图1所示)。白蚀区是由于裂纹面之间的摩擦而导致的微观结构变化[1, 2]。在滚动接触载荷下,裂纹可能扩展并最终到达滚道表面,进而导致表面剥落。
滚动接触疲劳中的材料缺陷
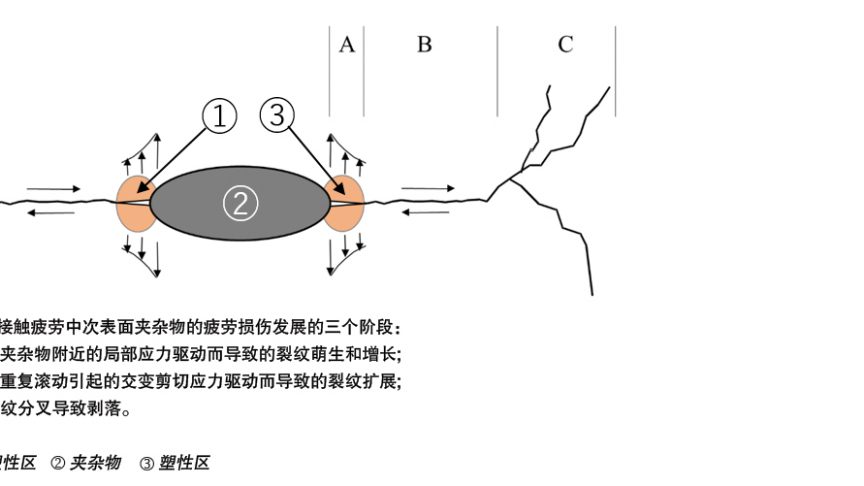
轴承滚道表面的滚动接触导致从表面延伸到表面下的循环应力。由于应力集中效应,即使在低于所谓的弹性安定极限的接触压力下(即低于该接触压力时,除夹杂物附近区域之外的整个材料处于弹性变形范围),夹杂物也会引起裂纹的萌生。如图2所示,损伤过程包括三个阶段,最终可能导致轴承滚道表面剥落。
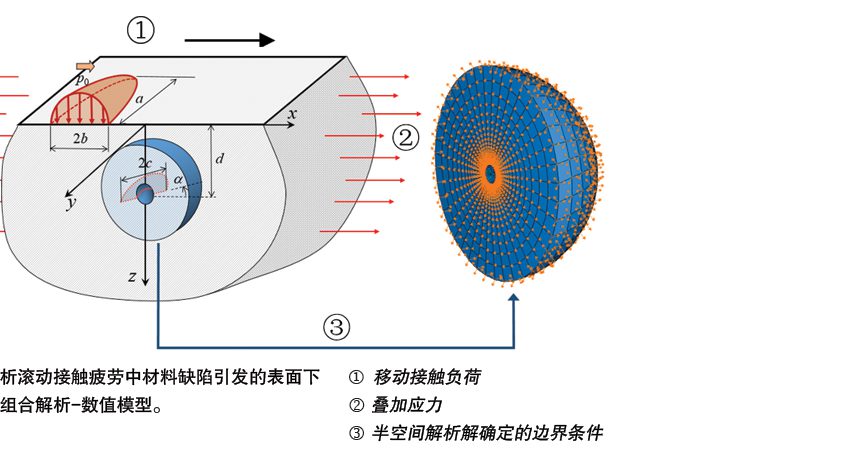
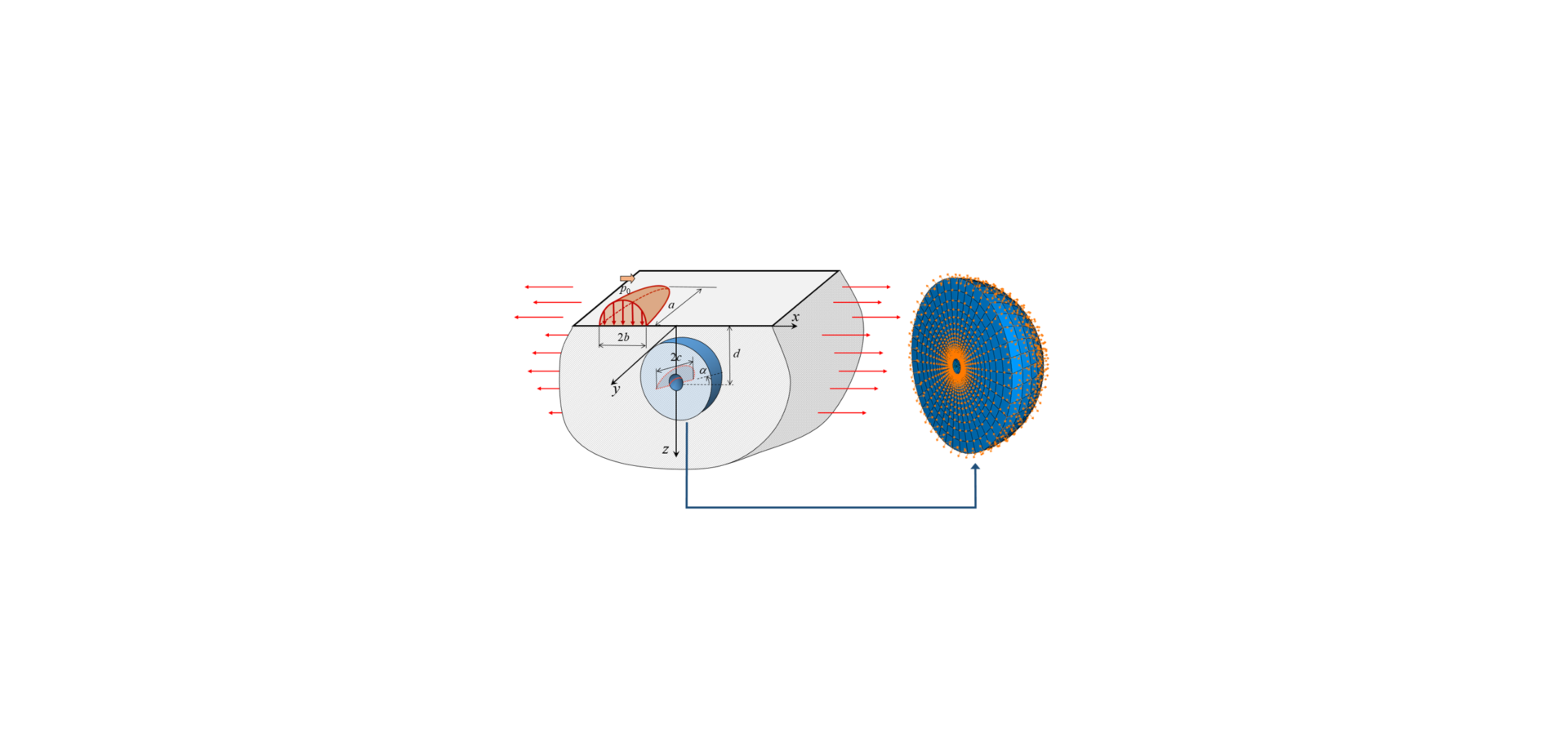
SKF已经开发了一种新的建模方法,将有限元法与承受表面负荷的半空间解析解结合起来。如图3所示,一层环绕缺陷的材料用有限元法仿真,而由滚动接触产生的表面下应力和变形由边界节点“传递”,在此处使用半空间解析解来确定位移[3]。
将组成或形态各异的不同类型的夹杂物,以及夹杂物和钢基体之间的粘连状况均考虑在内。有限元仿真还引入了轴承钢的弹塑性特性来描述局部材料的塑性变形。
图4显示了滚动接触疲劳下几种材料缺陷的计算应力增大系数,包括软质和硬质颗粒以及孔隙。这些颗粒被视为具有与钢基体不同刚度的弹性固体。图4还显示了每个夹杂物附近的冯米塞斯应力分布情况。完全粘合的夹杂物的应力增大系数相对较低。而与完全粘合的硬质夹杂物相比,完全粘合的软质颗粒的应力增大系数更高。应力增大系数随着夹杂物和钢基体之间的脱粘程度增大而增加。孔隙是具有最高应力增大系数的极端情况。
夹杂物附近的应力集中会引起钢的局部塑性,从而导致局部拉伸残余应力。拉伸残余应力连同夹杂物附近的其他局部应力,可能引发裂纹萌生和初始裂纹扩展,即图2所示的A阶段疲劳损伤。图4显示的应力提高程度,表示不同夹杂物的危害性。通常能够与轴承钢基体良好粘合的氮化钛颗粒,比氧化铝夹杂物的危害要低得多。氧化铝夹杂物也是硬质颗粒,但与钢基体的粘合性很差,甚至会发生脱粘。
在特定接触压力下,夹杂物裂纹的萌生主要取决于夹杂物附近的局部应力。换句话说,由于应力增大系数与夹杂物尺寸无关,所以控制裂纹萌生的是夹杂物的类型而非尺寸。然而,因夹杂物引发的裂纹并不总是会形成剥落。在某些情况下,裂纹可能会永久得到抑制。
对疲劳裂纹的扩展可在断裂力学框架内进行分析。疲劳裂纹扩展的驱动力可以根据裂纹的大小和夹杂物的具体类型,以及由赫兹接触产生的次表面应力和叠加应力(如残余应力、结构应力和/或环向应力等)来计算,如图3所示。如果驱动力超过一定的门槛值,则裂纹会扩展并导致失效。否则,该裂纹会得到抑制。驱动力越高,裂纹扩展越快。
例如,半径为R的球形夹杂物,其环形裂纹长度为 l,如图5所示。驱动力与p0 √(R + l)成正比,其中p0表示接触压力。这意味着驱动力随着接触压力的增加而增加。若p0为特定值时,夹杂物的尺寸(半径为R)控制裂纹扩展速度,尤其是在 l比R小得多的A阶段中。当裂纹从夹杂物扩散开来时,夹杂物的影响逐渐减弱。
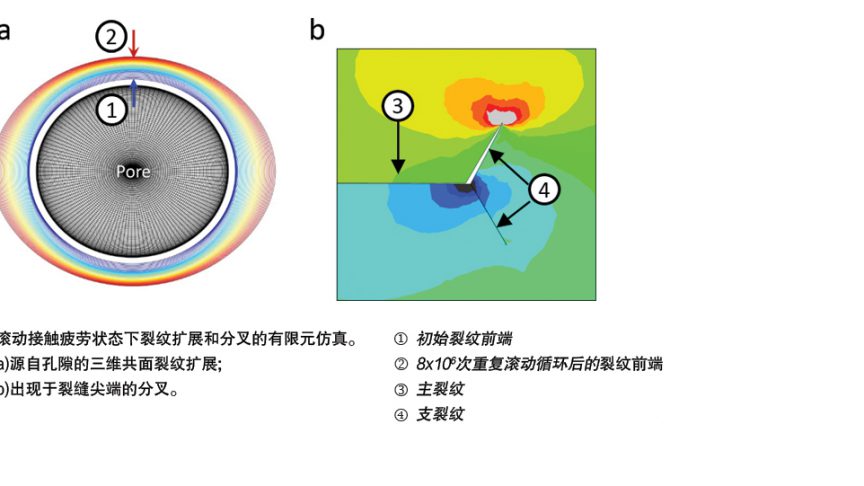
有限元分析法也用来模拟滚动接触疲劳状态下代表脱粘夹杂物的椭球形孔隙的3D裂纹扩展。图6a所示的仿真裂纹扩展与滚动接触疲劳实验观察到的裂纹形态的比较,表明预测和实验之间的定性是一致的。
B阶段的裂纹扩展主要由滚动接触产生的交变剪切应力驱动,迟早会导致C阶段的裂纹扩展,即由于裂纹尖端附近交替的拉伸-压缩应力区域产生的裂纹分叉(如图6b所示)。剪切模式共面裂纹扩展与拉伸模式裂纹分叉之间存在竞争。裂纹分叉的发生也会受到叠加应力的影响。拉伸应力促进裂纹分叉,从而可能降低疲劳寿命。而压缩应力是有益的,因为它往往能够抑制裂纹分叉。
图7显示了接触压力为2.5GPa而叠加应力不同时,球形夹杂物引起的裂纹扩展的驱动力与裂纹方向的函数关系。我们对不同方向裂纹的驱动力进行了评估。从图7可以看出,在没有叠加应力的情况下,裂纹方向为45˚时,驱动力达到峰值。如果施加200MPa的压缩应力,则驱动力曲线在30˚的角度达到其峰值。然而,如果施加200MPa的拉伸应力,则驱动力达到最大值时,裂纹方向增加到57˚。由此可见,拉伸应力可以加速裂纹扩展,而且往
往会使裂纹向陡峭的角度扩展;压缩应力则可能抑制裂纹扩展,往往导致裂纹向水平方向扩展。
工程意义
通过对疲劳机制的研究,我们找到了轴承过早失效的根本原因之一[2]。在实验室测试中,以白蚀裂纹和轴向裂纹为特征的轴承过早失效成功得到复制。在测试中,圆柱滚子轴承的内圈安装在带有人为波纹的套筒轴上。有限元仿真表明,诸如表面波纹等轴承座的形状偏差,会在内圈滚道附近产生拉伸应力。如果该应力超过一定极限,会削弱材料性能。如果再与赫兹应力相结合,就会导致因预先存在材料缺陷引发的裂纹的早期萌生及随后的加速扩展,进而导致轴承过早失效。
此外,对测试轴承圈的小间距连续剖面的金相检测表明,过早失效的轴承中常见的白蚀裂纹可从表面下夹杂物开始(如图8所示)。文献[4]报道的一项独立研究得出了类似的结论。这一发现的意义在于,它澄清了白蚀裂纹的起源问题。可以说,白蚀裂纹本质上是一种蝴蝶等形状的表面下裂纹。它可能从应力升高区萌生,并进一步发展。在滚动接触疲劳状态下,裂纹表面之间反复摩擦,可引起微结构逐渐变化,从而导致在裂纹表面附近形成白蚀区。因此白蚀裂纹或白蚀区不是造成轴承过早失效的原因,而是滚动接触疲劳损伤加剧的表现。
总结
对疲劳机制的研究对于推动轴承技术的发展至关重要,有助于应对来自严苛应用场合的挑战。研究证实,通过更深入地了解材料缺陷及其对轴承性能的影响,可以为一些问题找到新的思路,从而制定出能够降低轴承过早失效率的解决方案。此外,还可以确定材料缺陷的容限。
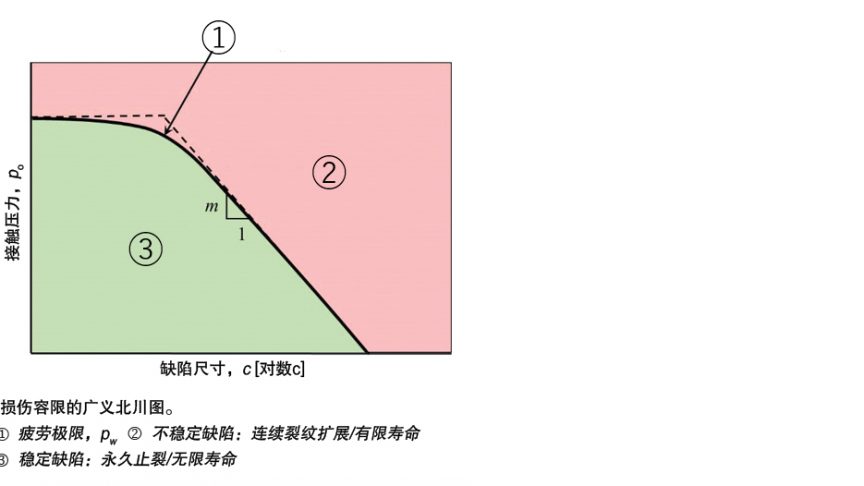
材料缺陷的容限可以通过广义的北川图来确定(如图9所示),在最大接触压力极限下的疲劳极限与缺陷尺寸有关。当缺陷变得非常小时,曲线接近基体材料的固有疲劳极限。对于较大缺陷,疲劳极限可以通过疲劳裂纹扩展开始的阈值条件来确定,即具有恒定斜率-m的渐近线,其中m的数值取决于缺陷的类型。
最初的北川[6]图是针对m =0.5的裂纹缺陷而提出的。广义北川图可应用于不同的材料和各种类型的缺陷。例如,它已经被用于确定混合陶瓷轴承氮化硅滚子表面缺损的容限[6]。在这类缺陷中,m的值为0.46。
基于对表面下夹杂物引起的疲劳裂纹萌生和扩展的研究,SKF开发了一个模型来预测轴承钢的极高周疲劳(VHCF)强度和疲劳极限[7]。结果表明[8],预计疲劳极限和极高周疲劳测试数据与ISO 281: 2007滚动轴承寿命标
准中设定的疲劳极限值恰好吻合。
参考文献
[1] W. Solano-Alverez, H.K.D.H. Bhadeshia, White-etching matter in bearing steel. Part II: Distinguishing cause and effect in bearing steel failure, Metall. Mater. Trans. A 45A (2014) 4916-4931.
[2] J. Lai, K. Stadler, Investigation on the mechanisms of white etching crack (WEC) formation in rolling contact fatigue and identification of a root cause for bearing premature failure, Wear 364-365 (2016) 244-256.
[3] J.L. Johnson, Contact Mechanics, Cambridge University Press, 1985, Cambridge, UK.
[4] M. Evans, White structure flaking failure in bearings under rolling contact fatigue, PhD Thesis, University of Southampton, UK, 2013.
[5] H. Kitagawa, S. Takahashi, Applicability of fracture mechanics to small cracks or cracks in the early stage. In: Proceedings of the second international conference on mechanical behaviour of materials. ASM, 1976, pp. 627-631.
[6] J. Lai, Y. Kadin, C. Vieillard, Characterization and modelling of the degradation of silicon nitride balls with surface missing-material defects under lubricated rolling contact conditions, Wear 398-399 (2018) 146-157.
[7] J. Lai, T. Lund, K. Ryden, A. Gabelli, I. Strandell, The fatigue limit of bearing steels – Part I: A pragmatic approach to predict very high cycle fatigue strength, Int. J. Fatigue 38 (2012) 155-168.
[8] A. Gabelli, J. Lai, T. Lund, K. Rydén, I. Strandell, G.E. Morales-Espejel, The fatigue limit of bearing steels – Part II: Characterization for life rating standards, Int. J. Fatigue 38 (2012) 169-180.