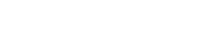The first part of this article was published in Evolution 2/98. This is the second and last part.For more than 100 years, researchers have looked at the factors that contribute to successful bearing operation through lubrication. We now know that the lubrication film required for good lubrication characteristics is extremely thin when compared with the roughness of the surfaces that are being separated.
To ensure that moving surfaces can work in a stable mode without wear or spalling, running conditions have to be ideal for each point on the lubricated surfaces at all times. This means that lubrication analysis has to take place at the actual region of contact between surfaces, elastically and plastically flattened to take a load. This is the asperity level.
It is not possible to predict the behaviour of a lubricated, elastically deformed region just by knowing the mean oil thickness and the mean contact pressure.
It is also necessary to know the local pressure, temperature, shear stress and lubricant rheology.

A simple steady-state calculation of the minimum oil film thickness above an asperity top shows that, if a rough surface is stationary and a smooth lubricated surface is rolling and sliding over it with local contact pressures above the glass transition pressure for the lubricant, the oil film thickness will fall to zero at each asperity top if enough time is available. A simple model of the lubricant in the glassy state is in the form of a solid with a given shear strength which varies with pressure and temperature. If the smooth surface then slides over the asperity, the film thickness will fall to:

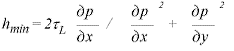
if enough time is available. This leads to oil film collapse on all the asperity tops with contact pressures above the glass transition pressure. The dynamic analysis of the compression of the asperities in the inlet zone and their re-appearance during the transport through the contact identified the important parameters that determine whether metallic contact takes place or not. In addition to contact pressure, these parameters are the surface roughness, the number of asperities inside the Hertzian contact area, the sliding speed, the transport time for an asperity through the lubricated contact and the mean oil film thickness. This could be summarised in the equation:

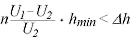
to avoid film collapse

where:
n	is the number of asperities from the inlet to the outlet of the lubricated contact
U1 and U2	are the surface speeds
hmin	is the mean oil film thickness
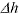	is the allowable elastic spring-back of the asperity during its passage through the contact.

This means that a surface with five wavelengths within the Hertzian contact can have the relative sliding speed:
(U1 – U2 )/ U1 = 0.44 = 44% for a given asperity spring-back while a surface with 36 asperities needs less than 10% slip for the same spring-back.
Analysis of these parameters shows that using the ratio between the calculated oil film thickness and the composite surface roughness as a measure of how well the surfaces are separated by an oil film will underestimate how well smooth surfaces are lubricated compared with rough surfaces. Smooth surfaces need not only proportionally thinner oil films for good lubrication but also the ratio of oil film thickness to surface roughness can be decreased.
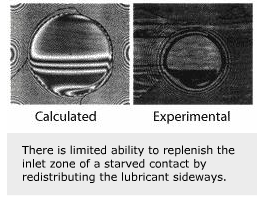
The non-Newtonian behaviour of the oil, manifested by a limiting shear strength, can lead to oil film collapse, as discussed above. This collapse can be studied by considering the solidified oil as a plastic solid and applying the extrusion theory. As expected, increasing sliding speeds and decreasing asperity wavelengths increase the likelihood of film collapse.

Starvation
Lubrication analysis generally assumes a sufficient supply of lubricant to ensure that the inlet to the contact is fully flooded. If this condition is not met and the contact is operating in the starved lubrication regime, then significant deviation from the predicted film thickness will occur.
Many machine elements operate in the starved regime; the conditions are particularly severe for grease lubricated bearings, and the accurate prediction of lubricating film thicknesses under these conditions is almost impossible.
In the starved condition, there is insufficient lubricant to fill the inlet and, as a result, the inlet does not experience the full hydrodynamic pressure build-up required to generate the high viscosity necessary to maintain full contact separation. This inevitably leads to lower film thicknesses than in the fully flooded condition. It is the inlet lubricant supply condition that determines the degrees of film reduction. It is not possible to predict this for many practical applications.
In early experimental studies, starved film thicknesses were measured using optical interferometry. As starvation increases and the inlet meniscus approaches the Hertzian radius, the film thickness drops below the lower detection limit of 100 nm, and it is impossible to quantify the fully starved condition. More recent experimental studies of the fully starved or parched regime, have shown that a thin film does persist, maintaining contact separation also when the meniscus reaches the Hertzian contact edge. The regime of parched lubrication was first proposed to denote the fully starved condition where there is no inlet meniscus. In the parched regime no free oil is present and only a thin oil film remains on the surface. It was shown that instrument bearings could run successfully for several hours with only 80-200 nm of deposited oil as lubricant. More direct evidence of residual film separation in the parched regime has been obtained with thin film optical interferometry measurements of heavily starved contacts.
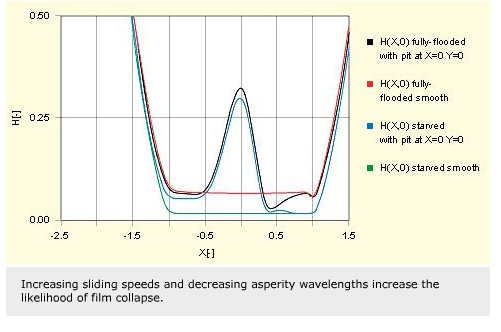
Experimental studies of film formation by greases in a model contact have shown that unless an external supply is used to replenish grease constantly within the raceway, it is rapidly pushed to either side of the raceway, thus starving the contact. Grease lubrication can be considered to be guided by a starvation phenomenon where the development of the EHL film is governed by the supply of lubricant from the surrounding grease reservoir. Initially EHL thickness increases with speed and then drops rapidly as the system passes through the speed/viscosity starvation boundary. The final speed-independent film thickness for the fully starved condition is approximately 40 nm.
This behaviour is characteristic for greases, although the starvation speed and final film thickness level vary greatly with different types of grease and operating conditions. The grease lubrication film has two components: a residual film of deposited gellant particles and a speed-dependent EHL contribution. Both components show a speed and time dependence, making prediction of film thickness in rolling contacts for a grease very difficult. In all cases the film thickness is dependent on test history and isolated results need to be interpreted with care.
There is limited ability to replenish the inlet zone of a starved contact by redistributing the lubricant sideways. Both the theoretical calculations and experiments give very stable lubrication over half a point contact while the other half is severely starved. Theoretical results show that side-flow is virtually non-existent in the high-pressure zone of pure rolling contacts.

Thin film lubrication
The lambda criterion provides a broad guide to the safe/unsafe operating limits for a lubricated contact. It cannot be used to assess operation at low lambda values; here the criterion is invalid. Under these conditions, the lambda value is far too crude a tool as paradoxically many systems are known to run successfully at low lambda ratios. This is particularly true for thin film lubrication where the estimated film thickness is less than the undeformed root mean square roughness value. Again the problem lies in being unable to predict with confidence the separating film thickness arising from the local contact conditions.
These analyses using the bulk basic properties of the lubricant do not allow prediction of the contact behaviour for low lambda application. Only when the calculated oil film thickness is large compared with the surface roughness, and no starvation effects are present, can the smooth surface approximation be used to predict the lubricant film thickness. As soon as the lubricated surfaces are not mathematically smooth and the roughness heights are not negligible compared with the mean oil film thickness, the local pressure fluctuation caused by the asperities will have an influence on the elastic deformations of the surface. This leads to sensitivity for roughness structure and directionality by the lubricated contact, as well as sensitivity to the amount of oil available for lubrication.
If the contact is starved because too little active lubricant is present, the normal EHL theory overestimates the film thickness if fully flooded results are used. At the same time, the local asperity pressure variation within the heavily loaded contact can partly flatten the roughness asperities, leading to smoother surfaces in the contact area.
For very smooth surfaces, the elastic deformation leads to an almost total conformity within the EHL contact and thus to a very high ratio of oil film thickness to roughness, even for very thin lubricant films. The calculated oil film thickness compared with the measured roughness of the surfaces cannot directly determine if a separating oil film is present in the contact or not. It depends both on the details of the surface structure and on the amount of lubricant available.
The mechanism describing how the last molecular layer of lubricant is removed from the surface tops and moves into the valleys in the structure or out from the contact still needs to be determined.

Bo Jacobson,
professor of machine elements at Lund Institute of Technology, Sweden, formerly with SKF Engineering & Research Centre B.V. (ERC) in Nieuwegein, the Netherlands.