The operation of a rotating machine at critical speeds frequently causes a high level of mechanical vibration, noise and excessive wear. An important objective regarding rotating machinery is either to eliminate major resonances or to avoid operating the equipment at speeds which could induce them.All shaft/bearing systems have a large number of frequencies at which they tend to vibrate. These are the so-called eigenfrequencies or natural frequencies. They are determined by the mass and stiffness distribution of the shaft as well as the location and stiffness of the supporting bearings. Sometimes the compliance of the housing also has a significant influence.

Each eigenfrequency is associated with a different vibration mode, or eigenmode. In practice, engineers are mainly concerned with the modes at lower frequencies, because their vibration amplitudes are more pronounced than those at higher frequencies.

Critical speeds

The rotor speed at which the shaft/bearing system is in resonance with a periodic excitation force is defined as a critical speed. The most common excitation force is due to mass unbalance which occurs at the rotor speed. At most speeds the vibration amplitudes of a shaft/bearing system will be small, except when the rotational speed, and thus the frequency of unbalance excitation, is near an eigenfrequency of the system, which will then respond with excessive vibrations.

Today’s sophisticated rotor dynamics programs can take into account the stiffness of shafts, bearings and housings. This enables engineers to design rotor bearing systems with critical speeds located away from the operational speed by a safe margin. Calculation of the undamped critical speeds and mode shapes is an excellent tool for preliminary evaluation of rotor bearing systems.

These values can only give relative displacements, however, and a complete unbalance response analysis is needed to determine absolute displacements. This is particularly important for start-up and shut-down phases when critical speeds are often passed. The risk of machine failure at those passages should be estimated.

In linear systems, the amplitude of the vibrations in resonance conditions depends mainly on the location and damping characteristics of the supporting bearings. While the stiffness of rolling element bearings is well understood in terms of external load and preload, little information is provided on the damping characteristics of a rolling bearing arrangement. In particular, there is no standardised procedure available to estimate damping in a rolling bearing arrangement using theoretical models.

Vibration models for rolling bearings

The performance of rolling element bearings is guaranteed only with sufficiently stiff housings and shafts. Tight support of thin and flexible bearing rings is important for correct bearing operation and to take advantage of high load carrying capacity.

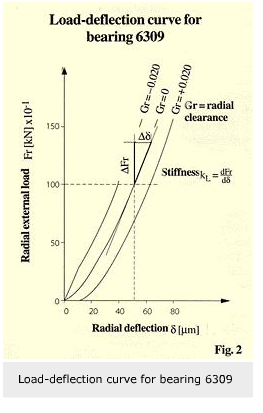
The weight of the rolling bearings is rather small in comparison to the dimensions of shafts and housings commonly used in mechanical engineering. In rotor-dynamics calculations, rolling bearings are therefore considered mainly as massless components. Bearing properties are often described by a linearised radial bearing stiffness (fig. 2) and a roughly estimated equivalent viscous damping coefficient.

For most accurate investigations a (5×5) bearing stiffness matrix can be calculated, including all translational and tilt stiffness terms as well as the cross-coupling terms.

Sources of bearing damping

Vibrations are excited by dynamic forces and mechanisms which occur in any rotating machine. Mechanisms which decrease the vibration amplitudes by converting vibration energy into energy which is not relevant for the vibrating system (e.g. heat) are called damping mechanisms.

Based on SKF knowledge and on the experiments described below, the following major sources for damping within a rolling bearing arrangement may be addressed (fig. 1):

Source #1 Damping of the elasto-hydrodynamic (EHD) lubrication film within the Hertzian contact zone between the rolling elements and the raceways.

Source #2 Bearing interface damping between the bearing rings and housings
or shaft respectively.

Source #3 Damping due to squeezing lubricant within the so-called entry
region where the oil is entrained into the Hertzian zone.

Source #4 Material damping due to Hertzian deformation of the rolling elements and raceways.

Test rig and parameter identification

The test rig is designed so that its dynamic behaviour is determined mainly by those parameters which are under consideration. In this case, stiffness and damping coefficients of the rolling bearing arrangements are the major parameters.

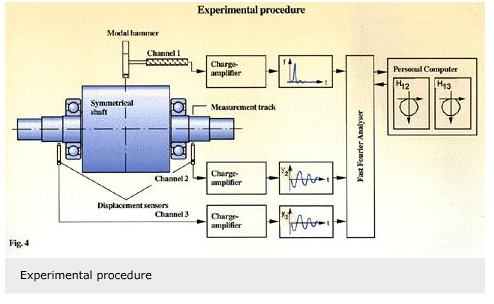
A pair of deep groove ball bearings 6309 are interference fitted to a heavy and very stiff symmetrical shaft. The assembly is then mounted into a very solid housing which is carried by a soft suspension (fig. 3 and 4). An experimental modal analysis verifies that the bearing arrangements represent the highest compliance in the system. All other parts (housing, shaft, preloading device etc.) behave as almost rigid bodies within the frequency range of interest, generating practically no additional structural damping.

Measured excitation forces and vibration response signals are used to calculate experimental frequency response functions, which represent the relationship between the input excitation force and the resulting vibration response (fig. 4).

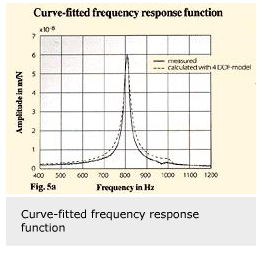
In order to identify bearing stiffness and damping coefficients, an analytical multi-degree of freedom model is used that simulates the measured dynamic rig behaviour. This analytical model incorporates the unknown bearing stiffness and damping values, which are identified by curve-fitting the calculated transfer functions to the measured ones with common least square techniques (fig. 5).

Experimental investigations

To separate experimentally the different damping mechanisms already mentioned, various test arrangements and operating conditions are applied. Experiments are carried out for various

• rotor speeds
• bearing preloads
• vibration excitation forces
• vibration excitation signals
• conditions of bearing lubrication
• conditions of housing to ring interface.

Experimental results

It is important to emphasise that the effectiveness of the mechanisms in dissipating energy depends on local compliance at their locations. For example, the experiments showed a high damping capacity of the EHD lubrication film (source #1) and even a higher damping capacity of the bearing interface (source #2). Owing to enormous stiffness values within the EHD layer and the bearing however, these mechanisms become fixed, and their high damping capacity cannot contribute to the overall damping of the rolling bearing arrangement. In case of vibrations, the major compliance occurs within the material of the rolling elements and the raceways, resulting in squeeze effects within the oil entry region. The damping mechanism within the material (hysteresis damping, source #4) and the damping mechanism within the oil entry region (source #3) predominantly determine the overall bearing damping.

For deep groove ball bearings, as well as for angular contact ball bearings, it was found that dry bearings without lubricant possess the lowest damping coefficients of all investigated conditions. The equivalent viscous damping coefficients are in the range of 330 Ns/m to 550 Ns/m.

Even the slightest amount of oil within the rolling contacts increases the bearing damping dramatically. The viscous damping coefficients for the non-rotating bearing for example, are identified to be in the range of 1,800 Ns/m to 2,100 Ns/m. With increasing rotor speed, the stiff EHD layer develops and fixes the damping mechanism within that zone. The values converge to the lower damping values of the lubricant-free bearing.

Theoretical approach

The identified minimum damping ability of a dry (lubricant-free) ball bearing can be estimated fairly accurately with a loss factor hvwhich is commonly applied in material damping theory. The empirical approach:

hv=DE_D/DE_V= 2Pf c/k

gives a simple relationship between the unknown bearing damping coefficient c and the bearing stiffness coefficient k which can be calculated. The term f describes the vibration frequency, DE_D the dissipated energy per load cycle and DE_V the maximum energy due to elastic deformation.

For a deep groove ball bearing 6309, the loss factor can be estimated with hv » 1%.

For angular contact ball bearings, a follow-up research programme was recently started at SKF Österreich AG and SKF ERC in co-operation with the Technical University of Vienna, Institute for Machine Dynamics and Measurements. Further damping data will soon be available for these bearing types.

Comparison of results

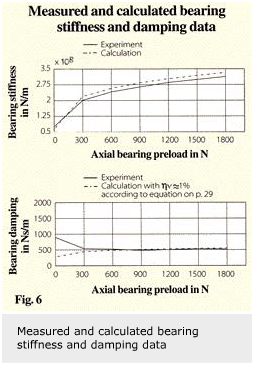
In this project the bearing stiffness and damping coefficients are obtained by experiments. This involves the risk of measuring unknown effects which may falsify the identification of the interesting bearing stiffness and damping values. For verification purposes, the bearing stiffness coefficients are calculated for all investigated operating conditions with proven SKF programs. An example of the close agreement between measured and calculated stiffness values is shown in figure 6. The data is shown in terms of axial bearing preload.

The lower half of figure 6 compares experimentally identified bearing damping values with those obtained by the theoretical approach described. Except for lightly preloaded bearings, the graph shows good correlation between measured and calculated values.

Rotor dynamics in practice

SKF has access to a series of sophisticated computer programs covering all needs in calculating the performance of rolling bearings in arbitrary applications. Static properties such as bearing deflections, contact stresses, load distributions or bearing stiffness values for any operating condition are calculated with a program developed by SKF. On special request from customers, finite element calculations and rotor dynamics calculations can also be carried out.

For rotor dynamic calculations an additional program is available. This program allows a comprehensive study of the dynamic behaviour of shaft/ bearing systems and is connected to a data base including all SKF standard bearings.

Recently, a customer experienced failures of SKF angular contact ball bearings mounted in air blowers after very short operating periods. Bearing defects could be excluded as the source of failure after investigations of the material, the heat treatment and the bearing dimensions. Static overloading of the bearings was also ruled out by means of simple calculations.

When the operating speed of the air blower was increased, dynamic problems were expected. Subsequent calculations with the rotor dynamics program showed that the lowest eigenfrequency (bending mode of shaft) was close to that of the operating speed. This was eventually verified by the customer through experiment. Applying the rotor dynamic program, the effect of an increased shaft diameter of one or more shaft sections, and the influence of the blower location on the dynamic behaviour of the entire system, could be estimated. This formed the basis for an improved air blower design.

Robert Zeillinger and Hubert Köttritsch,

SKF Österreich AG,

Steyr, Austria