Zudem sind Hybridlager für höhere Drehzahlen geeignet und haben bei gleichen Betriebsbedingungen meist eine wesentlich längere Lagerlebensdauer als gleich große Stahllager. Hybridlager sind auch bei hohen Beschleunigungen, Schwingungen und Schwenkbewegungen sehr gut einsetzbar. In Hochgeschwindigkeitsanwendungen, wie beispielsweise Werkzeugmaschinenspindeln und Turboladern, können spezielle Lagergeometrien, Werkstoffe und Schmiersysteme erforderlich sein. Es wird erwartet, dass dieser Trend anhält und die besonderen Eigenschaften von Hybridlagern zukünftig für viele moderne Industrieanwendungen entdeckt und genutzt werden.

Keramik als Wälzlagerwerkstoff wurde erstmals in den 1960er-Jahren bei Lagern für extreme Temperaturen in Luft- und Raumfahrtanwendungen eingesetzt. Durch Materialermüdungsversuche wurde nachgewiesen, dass stark verdichtetes, heiß gepresstes Siliziumnitrid im Vergleich zu anderen keramischen Werkstoffen die besten Wälzermüdungseigenschaften hat. Allerdings wurden auch bei scheinbar identischen Produktionschargen von Siliziumnitrid-Kugeln erhebliche Schwankungen im Ermüdungsverhalten festgestellt. In den 1980er-Jahren führten Lorösch und andere Wissenschaftler [4] Lebensdauertests an Hybrid-Schrägkugellagern durch. Sie verwendeten Wälzlagerkugeln, die gemäß der damals erhältlichen besten Siliziumnitrid-Qualität gefertigt waren, und fanden heraus, dass die Ermüdungsfestigkeit von Hybridlagern mit der von Stahllagern, die unter der gleichen Prüfbelastung getestet wurden, vergleichbar war – obwohl der Kontaktdruck bei Hybridlagern um ca. 12 Prozent höher ist. Ein weiterer Test einer zweiten Charge von Siliziumnitrid-Kugeln ergab jedoch eine geringere Ermüdungslebensdauer, was auf die schwankende Qualität der Keramikkugeln hinweist, welche für eine gute Ermüdungslebensdauer von Bedeutung ist.

Im Laufe der Jahre haben sich die Qualität und die Zuverlässigkeit von keramischen Wälzkörpern erheblich verbessert. Die Einführung von zerstörungsfreien Prüfverfahren und die ständigen Fortschritte in der Reinheit des Siliziumnitrid-Werkstoffs und der Sintertechnik ermöglichten es den Forschern schließlich, Siliziumnitrid-Kugeln mit einem zuverlässigen und gleichbleibenden Ermüdungsverhalten zu entwickeln [5]. Infolgedessen kam es in den 1990er-Jahren zu einem deutlichen Anstieg beim Einsatz von Hybridlagern in Hochgeschwindigkeitsspindeln von Werkzeugmaschinen; dies war mit erheblichen Vorteilen hinsichtlich der Drehzahleignung und Präzision dieser mechanischen Bauteile verbunden [6]. Bild 2 zeigt die Entwicklung der Ermüdungsfestigkeit des Keramikwerkstoffs [7], die sich auf ein verbessertes Warmpresssintern und eine kontinuierliche Reduzierung der Poren und Oberflächenfehler während des gesamten Herstellungsprozesses zurückführen lässt, welcher nun durch zerstörungsfreie Prüfverfahren überwacht und gesteuert werden konnte.

Ziel der aktuellen Forschung

Betrachtet man die Entwicklung von Hybridlagern, stellt man fest, dass die Ermüdungsfestigkeit von Siliziumnitrid für Wälzkörper in den letzten 20 Jahren enorme Fortschritte gemacht hat. Seit Anfang der 1980er-Jahre hat sich das Ermüdungsverhalten von Siliziumnitrid-Kugeln um zwei Zehnerpotenzen verbessert. Ermüdungslebensdauerversuche von Hybridlagern zeigen eindeutig, dass die keramischen Wälzkörper die zuverlässigsten Komponenten im Lagersystem sind. Dennoch kann die 12-%ige Erhöhung des Kontaktdrucks bei Hybridlagern in manchen Betriebsbedingungen zu Ermüdungsschäden unterhalb der Oberfläche führen, was die Lebensdauer des Lagers begrenzt. Bild 3a zeigt das Weibull-Wahrscheinlichkeitsdiagramm der von Forster und anderen Wissenschaftlern [8] durchgeführten Lebensdauertests von Hybrid- und Stahllagern, die unter den gleichen Prüfbedingungen getestet wurden. Das Diagramm zeigt, dass bei hoher Belastung und günstigen Schmierbedingungen Ermüdungsschäden unterhalb der Oberfläche das Ermüdungsverhalten von Wälzlagern maßgeblich beeinflussen. Bei Hybridlagern, die einem hohen Kontaktdruck (3,5 GPa) ausgesetzt sind, ist daher nach einer bestimmten Laufzeit die Ausfallwahrscheinlichkeit höher als bei Stahllagern, die bei vergleichbarer Prüflast und damit einem Kontaktdruck von 3,1 GPa getestet wurden. (Hinweis: Aufgrund der Überschneidung des 90 %-Vertrauensbalkens im Weibull-Diagramm von Bild 3a wird dies mit einer niedrigen statistischen Signifikanz erreicht.)

Bild 3b zeigt das Weibull-Wahrscheinlichkeitsdiagramm der von Chiu und anderen Forschern [9] durchgeführten Lebensdauertests, bei denen Hybrid- und Stahllager unter gleichen Prüfbedingungen miteinander verglichen wurden. Der Test wurde mit einer niedrigeren Belastung durchgeführt, wobei ein maximaler Hertz’scher Kontaktdruck von 2,6 GPa bei der Hybrid-Ausführung und 2,3 GPa bei der Stahlvariante entstand. Die Prüfung fand unter schwierigen Umgebungsbedingungen statt: Hohe Temperaturen, geringe Schmierfilmdicke und Einlauf mit durch Partikel verunreinigtem Schmieröl sollten die tatsächlichen Schmierverhältnisse der Anwendung simulieren.

Modellierungsansatz

In Referenz [1] wurde eine generalisierte Lebensdauergleichung mit getrennten Termen für die Bereiche auf und unterhalb der Oberfläche entwickelt (Bild 4). Dabei ist zu beachten, dass die in Anzahl von Umdrehungen angegebene Lebensdauer L des Wälzlagers durch die Relation L=N/u auf die Anzahl der Lastzyklen N umgerechnet werden kann, wobei u für die Anzahl der Lastzyklen steht, die bei jeder Umdrehung auftreten.

Bei Wälzlagerlebensdauerberechnungen wird eine standardisierte Steigung der Weibull-Geraden verwendet, wobei e vorgegeben werden kann. L₁₀ steht für eine Lagerlebensdauer von 10 %, was ein 90-%iges Überleben des Lagers S=0,9 bedeutet; die Lebensdauergleichung kann als Gleichung (1) geschrieben werden:

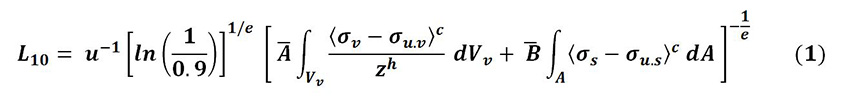
Gleichung (1) stellt die Basis für ein generalisiertes Lagerlebensdauermodell dar, das die Akkumulation der Schäden an der Oberfläche eindeutig vom akkumulierten Ermüdungsschaden unterhalb der Oberfläche trennt. Der den Bereich unterhalb der Oberfläche betreffende Term der Gleichung (1), dargestellt durch das Volumenintegral, kann, wie in Referenz [1] erläutert, mit den gängigen Wälzermüdungsverfahren gelöst werden.

Der durch das Flächenintegral der Gleichung (1) vorgegebene Term für den Bereich auf der Oberfläche muss jedoch auf andere Weise quantifiziert werden. Seine Bewertung erfordert die Abschätzung des Schadens, dem das Lager, aufgrund tatsächlich auftretender Spannungszustände unter einer Vielzahl möglicher Betriebszustände, ausgesetzt sein kann.

Diese Aufgabe ist komplex, bietet aber die Möglichkeit, tribologische Phänomene von Keramik-Stahl-Laufbahnkontakten zu charakterisieren und deren Einfluss auf die Lebensdauer von Hybridlagern, wie in [2] beschrieben, zu quantifizieren.

Überlebenswahrscheinlichkeit von Keramik-Stahl-Kontaktflächen

Gleichung (1) kann so umgeschrieben werden, dass die Trennung zwischen den jeweiligen Anteilen der Bereiche auf und unterhalb der Laufbahnoberfläche deutlich erkennbar wird: Gleichung (2).

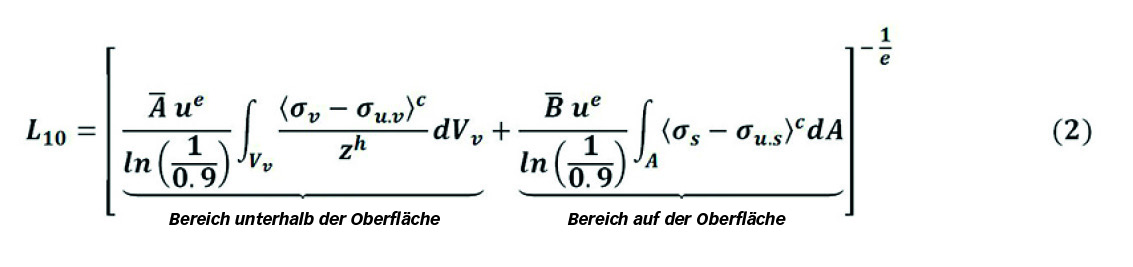
Bei einer gegebenen Lagergröße und unter Ausschluss konstanter Terme ist der Teil des Oberflächenermüdungsschadens von Gleichung (2) direkt abhängig von den kombinierten Einflüssen der Spannungszustände, die beim Überrollen des Wälzkontakts an der Laufbahnoberfläche auftreten: Gleichung (3).

Die Bewertung des Oberflächenschadensintegrals (3) kann durch Einbeziehung der von der Laufbahnoberfläche ausgehenden Spannungen erfolgen, die sich aus den unterschiedlichsten Betriebsbedingungen des Lagers ergeben.

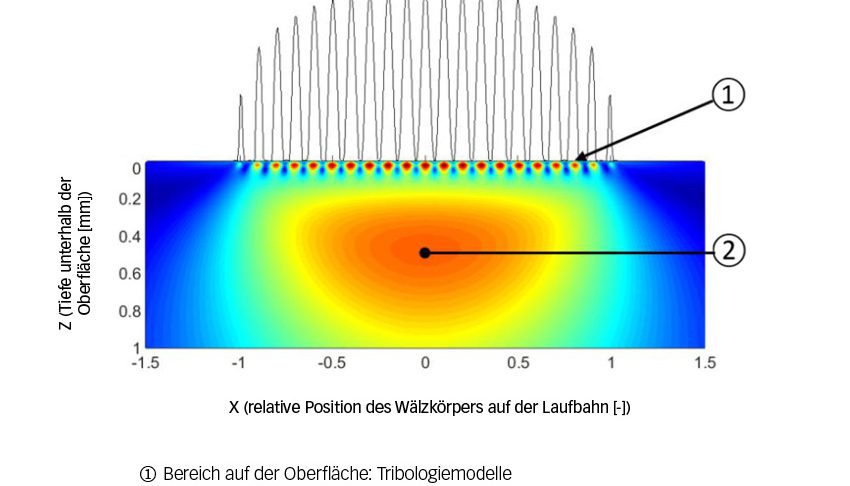
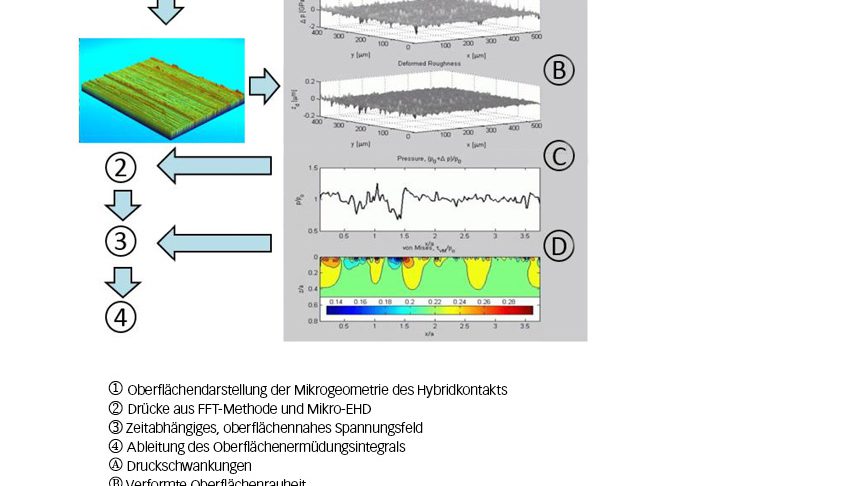
In der aktuellen Fassung können Spannungen und die Schadensakkumulation auf der Oberfläche mit einem Oberflächenzerrüttungsmodell für elastohydrodynamische (EHD), geschmierte, raue Roll-/Gleitkontakte, beispielsweise einem Mikro-EHD-Modell nach Referenz [10], abgebildet werden. Mit diesem Ansatz können auch Grenzschmierbedingungen und vorhandene Eindrückungen berücksichtigt werden, wobei 3D-Oberflächenabbildungen der Laufbahnrauheit (einschließlich der Eindruckmikrogeometrie) benötigt werden (Bild 5).

Lagerlebensdauerberechnungen, die sowohl Oberflächenspannungen als auch Mikro-EHD-Modelle nutzen können zeitaufwändig und damit in der täglichen Anwendung unpraktisch sein. Daher wurden Parameterstudien durchgeführt, um eine vereinfachte analytische Gleichung abzuleiten, die eine schnelle Abschätzung der Oberflächenermüdungsschäden von Hybridlagern unter den gegebenen Betriebsbedingungen der jeweiligen Lageranwendung ermöglicht. Zu diesem Zweck wurden mehrere Oberflächentopografien der Lagerlaufbahn mit optischen 3D-Messverfahren (Interferometrie) erstellt (Bild 5).

Für diese Untersuchungen wurden rund 100 Oberflächen von Hybrid-Rillenkugellagern, Hybrid-Schrägkugellagern und Hybrid-Zylinderrollenlagern gescannt. Die Proben umfassten Lagerlaufbahnen, die unter verschiedenen Umgebungsbedingungen, also sauberen und verschmutzten Schmierbedingungen, eingelaufen wurden.

Mit den erfassten Oberflächenmikrogeometrien wurden mehrere numerische Simulationen des Oberflächenermüdungsspannungsintegrals von Hybridkontakten durchgeführt. Der Einfluss der Schmierstoffverschmutzung wurde durch die Verwendung von Eindrucktopografien infolge von lokal auf die Oberfläche wirkenden Beanspruchungen in die Simulationen einbezogen. Schmierbedingungen des Lagers wurden durch transiente Mikro-EHD-Simulationen des Wälzkontaktes für unterschiedliche Schmierfilmdicken berücksichtigt.

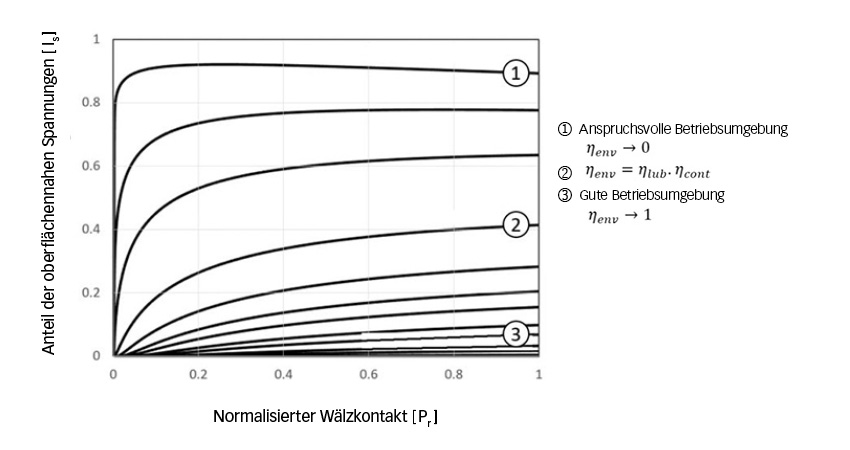
Die numerischen Ergebnisse der Parameterstudien des Oberflächenermüdungsspannungsintegrals von Hybridlagern wiesen auf die Möglichkeit hin, diese Größe durch eine analytische Formulierung darzustellen. Es wurde festgestellt, dass alle numerischen Ergebnisse mit einer Exponentialfunktion gut approximiert werden können. Diese Funktion hängt im Wesentlichen von zwei Hauptparametern ab: der relativen Belastung P_r = P/P_u  des Wälzkontakts und dem umgebungsabhängigen Schmierungsbeiwert der Anwendung η_env = η_lub ∙ η_cont , Gleichung (4):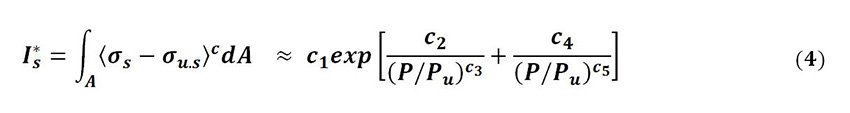

Die Terme c₁⋯c_n von Gleichung (4) sind abhängig von den Umgebungsbedingungen der Anwendung (η_env), die sich unmittelbar aus der Schmierung (η_lub) und den Verunreinigungsbeiwerten (η_cont) ergeben.

Anwendung des Modells

Das Generalized Bearing Life Model aus Gleichung (4) kann angewendet werden, um die vorstehend behandelten Lebensdauertestdaten von Forster [8] und Chiu [9] nachzurechnen.
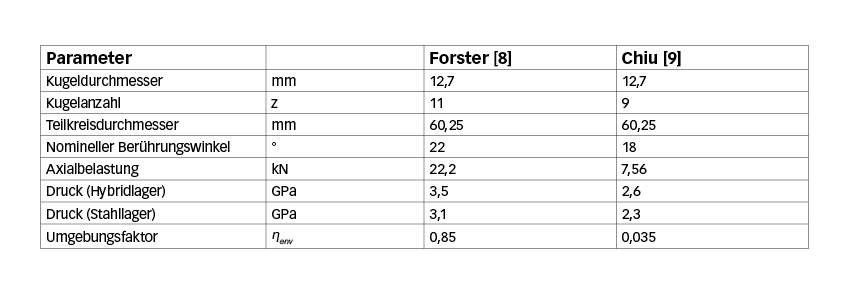
Die Tests wurden an Schrägkugellagern der Lagergröße 7208 durchgeführt. Dabei wurden insgesamt 40 Hybridlager getestet, wobei es zu 12 Ausfällen kam. Bei den Stahlvarianten wurden 32 Lager Lebensdauertests unterzogen, die zu 21 Ausfällen führten. Die geometrischen Angaben zu den Prüflagern und die jeweiligen Lasten und Spannungszustände der Lebensdauertests sind in Tabelle 1 dargestellt.

Ein wesentlicher Unterschied zwischen den beiden Tests ergibt sich aus den Lasten und dem Schmierungszustand, unter denen die Tests durchgeführt wurden. Bei den Lebensdauerprüfungen nach Forster war die Last höher, was bei der Hybridlagervariante zu einem Hertz’schen Kontaktdruck von 3,5 GPa führte. Das Ölumlaufsystem war mit einer guten Filtration ausgestattet. Zudem waren die Schmierbedingungen mit einem Kappawert von etwa 2,5 gut. Der aus den gegebenen Schmierbedingungen resultierende GBLM-Umgebungsfaktor liegt entsprechend bei η_env=0,85. Daraus resultiert ein geringer Schädigungsanteil durch Spannungen an der Oberfläche, bezogen auf den akkumulierten Gesamtschaden. Unter diesen Betriebsbedingungen dominiert die Werkstoffermüdung unterhalb der Oberfläche als Ausfallmechanismus. Daher sind die Betriebsbedingungen des Forster-Tests für die Stahllagervariante 7208 vorteilhaft, da aufgrund der geringeren Hertz’schen Spannung von 3,1 GPa ein geringerer Ermüdungsschaden im Materialvolumen unter der Oberfläche entsteht.

Bei den Lebensdauertests nach Chiu war die aufgebrachte Last deutlich geringer, was bei der Hybridlagervariante zu einer maximalen Hertz’schen Spannung von 2,6 GPa führte. Die Betriebstemperatur bei den Tests war höher (150 ^oC), was ungünstigere Schmierbedingungen für die Lager zur Folge hatte. Ferner wurden die Tests mit induzierten Laufbahnfehlern durchgeführt, um die typischen Verschmutzungsbedingungen zu reproduzieren, die in vielen Lageranwendungen anzutreffen sind. Dies wurde erreicht, indem man die Lager 15 Minuten lang in Öl mit 2,5 ppm Aluminiumoxidpartikeln mit einer Größe von 20 µm einlaufen ließ. Der sich hieraus ergebende GBLM-Umgebungsfaktor, der die gegebenen Betriebsbedingungen charakterisiert, ist in diesem Fall niedrig, d. h., η_env=0,035.

Bei den Lebensdauertests nach Chiu ist bei den gegebenen Belastungs- und Umgebungsbedingungen die Rolle der Oberflächenermüdungsfestigkeit ausschlaggebend für das Überleben des Lagers. Die durch Spannungen an der Oberfläche hervorgerufene Ermüdung dominiert entsprechend das Ermüdungsverhalten des Wälzlagers. Der speziell für Hybridlager entwickelte Oberflächenspannungsindex bewirkt an dieser Stelle die höhere Ermüdungsfestigkeit für Hybridlager und kompensiert die höhere Hertz’sche Spannung (2,6 GPa) im Keramik-Stahl-Kontakt.

Basierend auf den beschriebenen Betriebsbedingungen der Lebensdauertests von Hybridlagern wurde mit Hilfe einer Prototypen-Software die Lebensdauer nach GBLM berechnet. Die Lebensdauer der Stahlvariante des Schrägkugellagers 7208 wurde ebenfalls, wie in Referenz [1] beschrieben, mit einer vergleichbaren Version von GBLM berechnet. Die Ergebnisse der rechnerischen Lebensdauer bei 90-%iger Erlebenswahrscheinlichkeit der verschiedenen Lagervarianten und Testbedingungen sind in den Weibull-Diagrammen von Bild 7a und 7b enthalten. Die rechnerischen Lebensdauern in Millionen Umdrehungen sind in den Diagrammen mit dünnen vertikalen Linien dargestellt, die entsprechend der jeweils berechneten Lagervariante gekennzeichnet sind.

Die Untersuchung der Ergebnisse des GBLM-Modells ist unter Bezugnahme auf Forsters Testergebnisse in Bild 7a dargestellt. Das Diagramm zeigt, dass sich die rechnerischen Lebensdauern für die Hybrid- und Stahlvarianten etwa am unteren Ende des 90 %-Vertrauensbereichs der 10 %-Versagenswahrscheinlichkeit der Lebensdauertestergebnisse bewegen. Das bedeutet, dass Forsters Lebensdauertests die Ergebnisse des GBLM mit hoher statistischer Signifikanz bestätigen.