Les imperfections des matériaux
Chez SKF, la recherche est depuis toujours tournée vers une meilleure compréhension des effets de la micro-structure et des imperfections préexistantes du matériau sur les performances des roulements. Les travaux présentés ici sont essentiels pour définir les caractéristiques et les classes de sévérité associées qui influent de façon décisive sur les performances des roulements.
De nos jours, les avaries de roulements dues à la fatigue de contact de roulement (FCR) sont plutôt rares et, généralement, la durée de service réelle des roulements dépasse largement la durée nominale théorique. Il arrive cependant que des roulements utilisés dans des applications spécifiques soient victimes d’avaries prématurées. La compréhension des mécanismes de défaillance des roulements joue un rôle essentiel dans l’amélioration continue de leurs performances en réponse aux besoins d’une densité de puissance toujours plus élevée au sein d’applications modernes.
La fiabilité des roulements dans diverses applications obéit au principe du maillon le plus faible, autrement dit l’avarie est causée par la rupture du maillon le plus faible du système en question. Dans des conditions de lubrification médiocre, l’avarie peut être due à une altération de la surface sous forme de fatigue de surface ou d’usure. Sinon, le maillon faible peut se situer en sous-couche. Cela s’explique par le fait que la contrainte maximale de cisaillement induite par le contact hertzien est atteinte à une certaine profondeur sous la surface des pistes. Par ailleurs, à l’instar de la plupart des matériaux haute résistance, les aciers pour roulements peuvent présenter une sensibilité aux imperfections préexistantes du matériau, comme les inclusions non-métalliques issues des procédés de production sidérurgiques.
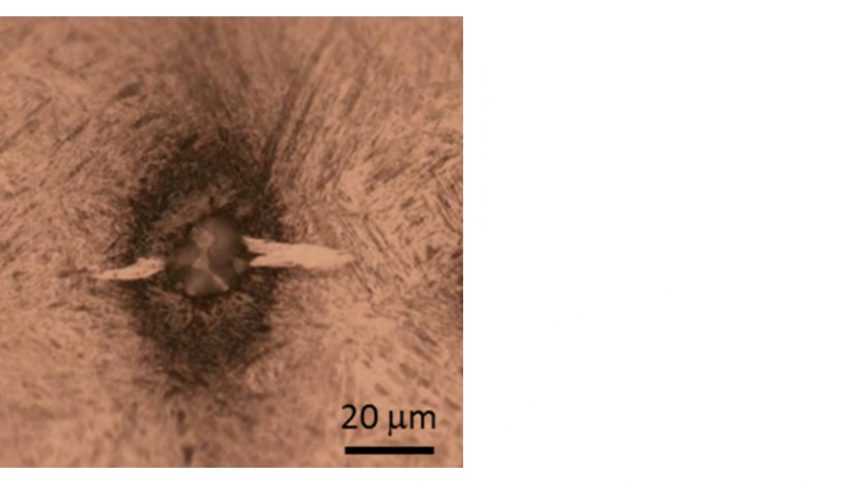
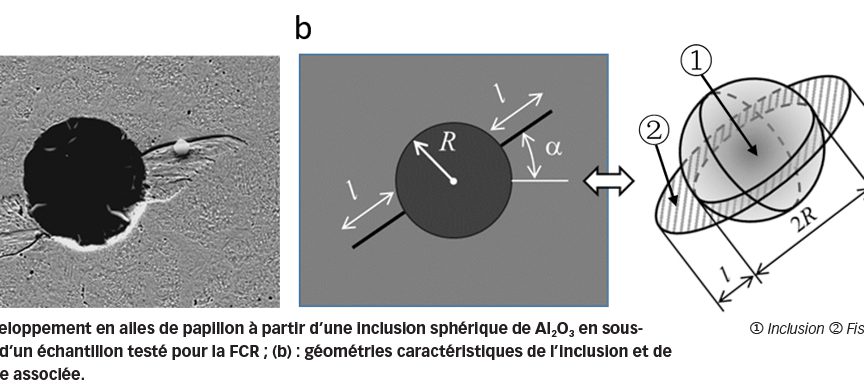
Des études métallographiques d’échantillons testés pour la FCR indiquent que ces formations dites en « ailes de papillon » se développent souvent à partir d’inclusions non-métalliques. L’attaque chimique au Nital révèle un faciès en forme « d’ailes de papillon ». On observe sur cet échantillon, au microscope optique, une paire de fissures qui partent d’une inclusion avec une zone de phase blanche, comme illustré par la Fig. 1. La zone de phase blanche correspond à une altération de la microstructure due au frottement entre les faces des fissures [1, 2]. Sous l’effet de la charge du contact de roulement, la fissure est susceptible de se propager jusqu’à atteindre la surface des pistes et provoquer un écaillage de celles-ci.
Imperfections des matériaux et FCR
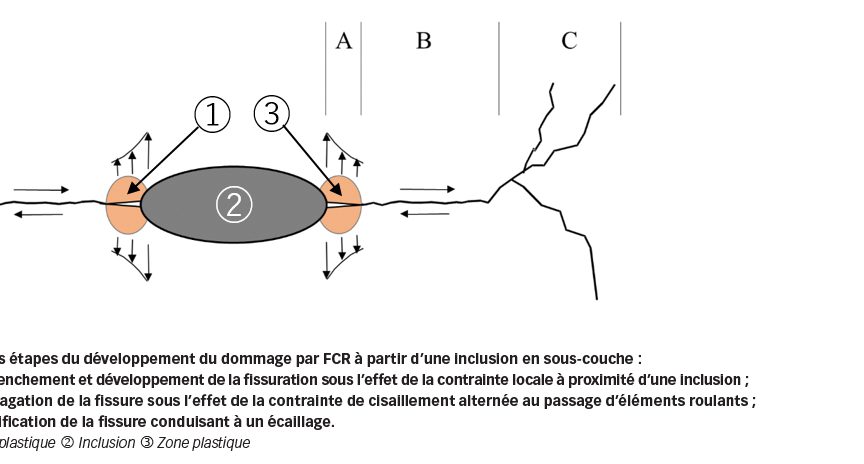
Le contact de roulement sur les surfaces des pistes se traduit par des contraintes cycliques qui s’étendent de la surface vers la sous-couche. Sous l’effet de la concentration de contraintes, des fissures peuvent être initiées au niveau d’inclusions, y compris sous une pression de contact inférieure à la limite élastique, c’est-à-dire la pression de contact sous laquelle le matériau dans sa globalité, à l’exception des régions proches des inclusions, présente un comportement élastique. Comme le montre la Fig. 2, le processus d’altération se déroule en trois étapes pouvant conduire à un écaillage de la surface des pistes du roulement.
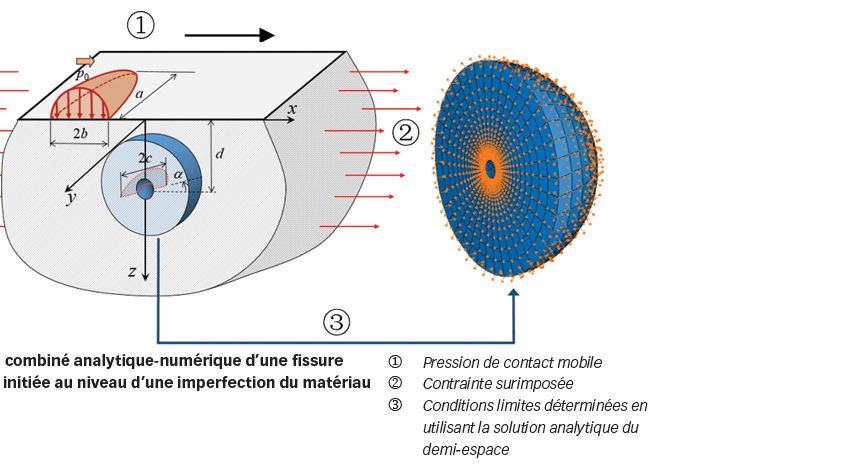
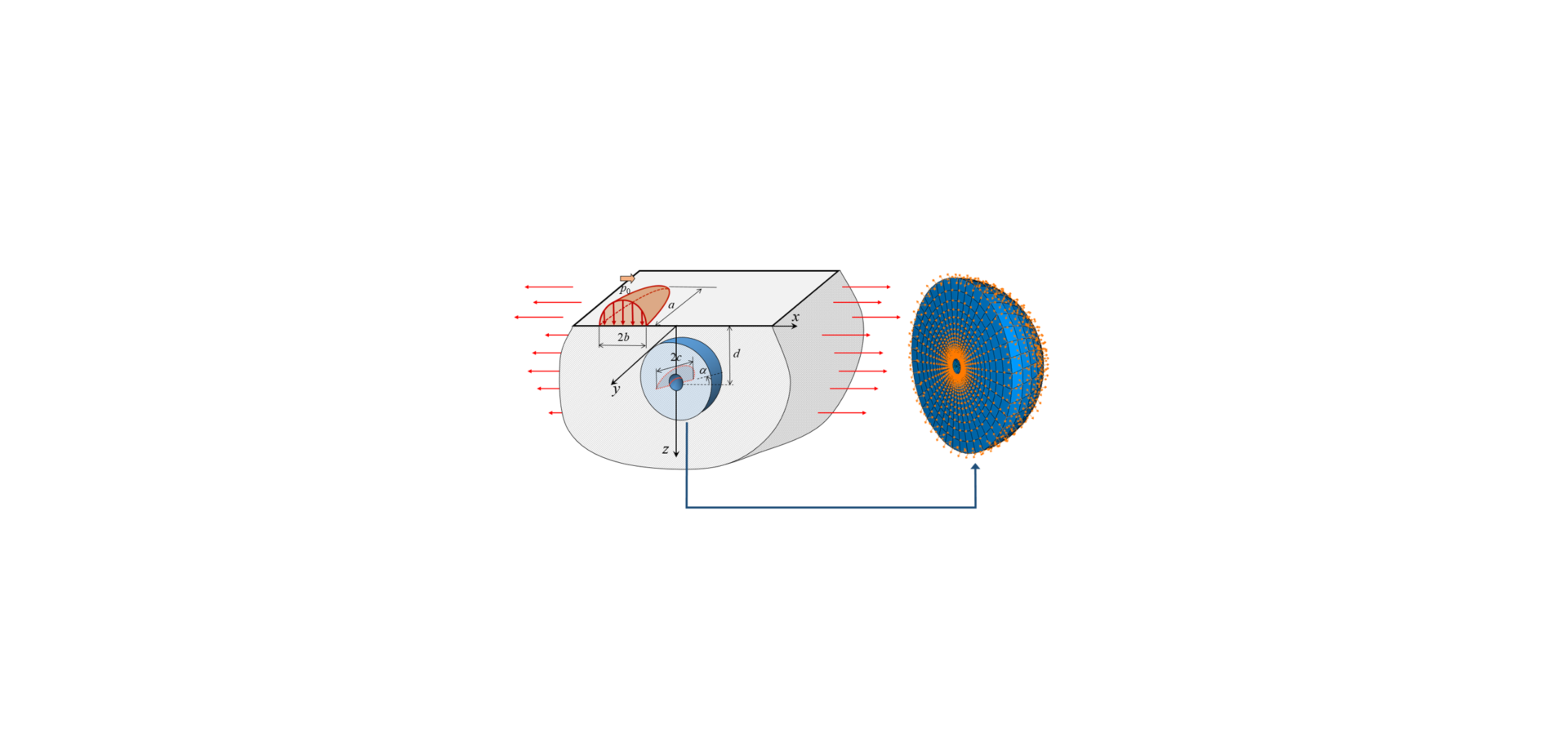
Une nouvelle méthodologie de modélisation a été mise au point. Elle combine la méthode des éléments finis (EF) avec une solution analytique basée sur un demi-espace soumis à une pression de contact. Comme le montre la Fig. 3, une couche de matériau autour du défaut est modélisée selon la méthode des EF, tandis que les contraintes internes et la déformation découlant du contact de roulement sont « transmises » par des conditions limites, au niveau desquels les déplacements sont calculés en utilisant la solution analytique du demi-espace [3].
Il convient de prendre en compte différents types d’inclusions, en termes de composition ou de morphologie, ainsi que l’état de la liaison entre les inclusions et la matrice en acier. La simulation par EF inclut également le comportement élasto-plastique des aciers pour roulements afin de tenir compte de la plasticité locale.
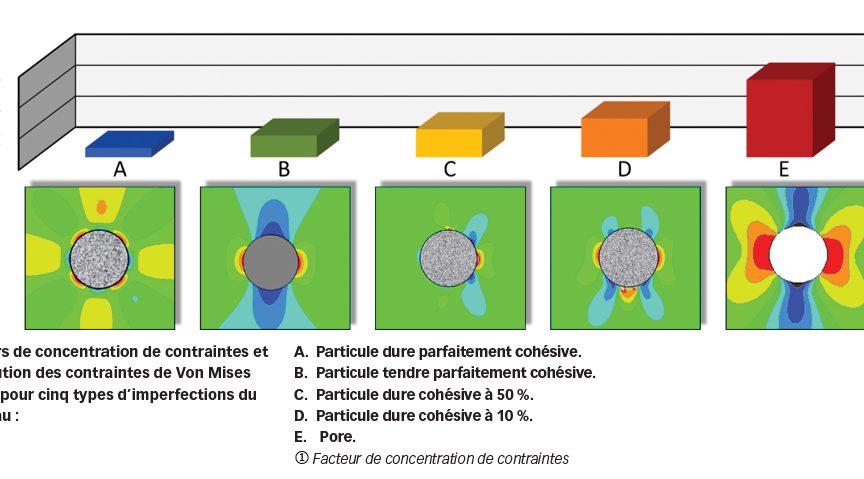
La Fig. 4 représente les facteurs de concentration de contraintes relatifs à diverses imperfections du matériau (particule tendre, particule dure et pore) en FCR. Les particules sont considérées comme des solides élastiques de rigidité différente de celle de la matrice en acier. La Fig. 4 montre également la distribution des contraintes de Von Mises à proximité de chaque inclusion. Pour une inclusion parfaitement cohésive, le facteur de concentration de contraintes est relativement faible. Il sera supérieur pour une particule tendre par rapport à une particule dure. Le facteur de concentration de contraintes augmente avec la perte de liaison entre l’inclusion et la matrice en acier. Un pore constitue le cas extrême caractérisé par le facteur de concentration de contraintes le plus élevé.
La concentration des contraintes à proximité d’une inclusion peut induire une plasticité locale de l’acier qui se traduit par une contrainte de traction résiduelle localisée. Cette contrainte de traction résiduelle, combinée à d’autres composantes de la contrainte locale à proximité de l’inclusion, peut déclencher la fissuration et entraîner la propagation initiale de la fissure, ce qui correspond au stade A du dommage par fatigue illustré par la Fig. 2. Le niveau de concentration de contraintes sur la Fig. 4 est un indicateur de la nocivité des différentes inclusions. Les particules de nitrure de titane, qui présentent généralement une bonne cohésion avec la matrice en acier du roulement, se révèlent ainsi beaucoup moins nocives que les inclusions en oxyde d’aluminium, qui sont également des particules dures mais présentent une faible cohésion, voire une perte de liaison, avec la matrice en acier.
Sous une pression de contact spécifique, le déclenchement de la fissuration à partir d’une inclusion dépend principalement de la contrainte locale à proximité de l’inclusion. En d’autres termes, le déclenchement de la fissuration est régi non pas par la taille mais par le type de l’inclusion, puisque le facteur de concentration de contraintes n’est pas lié à la taille de l’inclusion. Cependant, une fissure initiée au niveau d’une inclusion n’évolue pas toujours vers un écaillage. Dans certaines circonstances, la fissure peut être définitivement stoppée.
Le développement de la fissuration de fatigue est analysé dans le cadre de la mécanique des ruptures. La force motrice du développement de la fissuration de fatigue peut être calculée en tenant compte de la taille de la fissure et de celle de l’inclusion d’un certain type, ainsi que de la contrainte interne résultant du contact hertzien et des contraintes surimposées, telles que les contraintes résiduelles, structurelles et/ou circonférentielles, comme illustré par la Fig. 3. Au-delà d’une certaine valeur de la force motrice, la fissure se propage jusqu’à l’avarie. En dessous de cette valeur, la fissure est stoppée. Plus la force motrice est élevée, plus la propagation de la fissure est rapide.
Prenons, par exemple, une inclusion sphérique de rayon R, présentant une fissure annulaire, de longueur l, comme représentée sur la Fig. 5. La force motrice est proportionnelle à p0 √(R+l), où p0 correspond à la pression de contact. Autrement dit, la force motrice augmente avec la pression de contact. Pour une pression p0 donnée, la taille de l’inclusion, R, détermine la vitesse de développement de la fissure, en particulier au stade A où l est inférieure à R. L’influence de l’inclusion diminue à mesure que la fissure se propage à distance de l’inclusion.
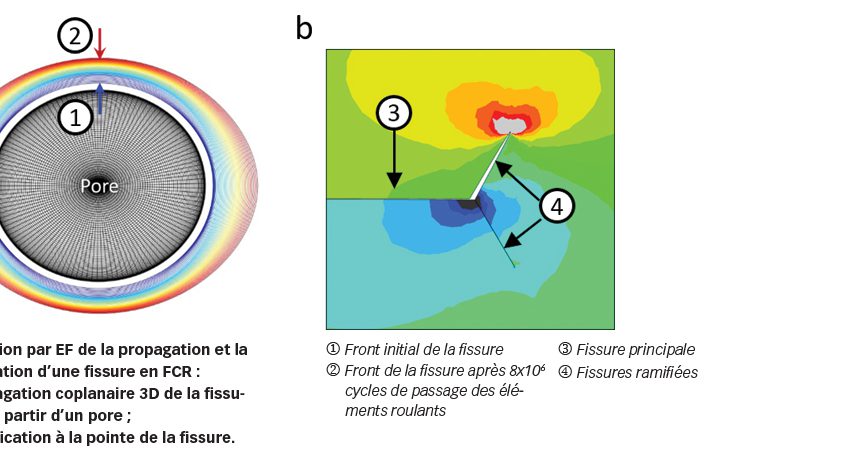
Une analyse par éléments finis a été réalisée afin de simuler la propagation en 3D d’une fissure à partir d’un pore ellipsoïdal représentant une inclusion de faible cohésion en FCR. La propagation simulée, représentée sur la Fig. 6a, a ensuite été comparée à la configuration des fissures observées dans des expériences de FCR. Il en ressort une bonne concordance qualitative entre résultats numériques et expérimentaux.
Au stade B, la fissure se propage principalement sous l’impulsion de la contrainte de cisaillement alterné résultant du contact de roulement, ce qui débouche à plus ou moins long terme sur le stade C de la propagation, à savoir une ramification de la fissure due à une zone de contrainte alternée de tension-compression à proximité de la pointe de la fissure, comme illustré par la Fig. 6b. Le développement coplanaire de la fissuration en mode cisaillement et la ramification de la fissure en mode traction sont en concurrence. Le déclenchement de la ramification peut être perturbé par les contraintes surimposées. Une contrainte de traction favorise la ramification et peut réduire la durée en fatigue. Une contrainte de compression est bénéfique car elle tend à empêcher la ramification.
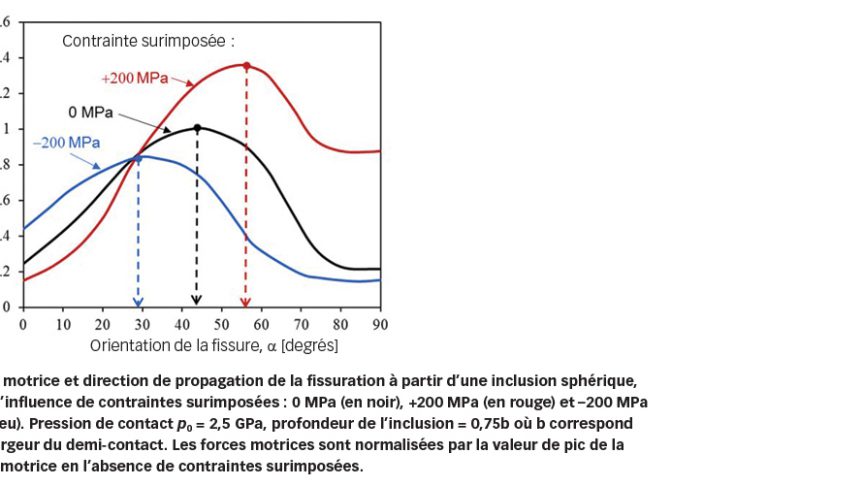
La Fig. 7 illustre la relation entre la force motrice de propagation de la fissuration à partir d’une inclusion sphérique et l’orientation de la fissure, pour une pression de contact de 2,5 GPa et différents niveaux de contraintes surimposées. Les forces motrices ont été évaluées selon différentes orientations de la fissure. On observe qu’en l’absence de contraintes surimposées, la force motrice maximale correspond à une orientation de la fissure de 45°. Si une contrainte de compression de 200 MPa est appliquée, le sommet de la courbe de la force motrice correspond à une orientation de 30° ; en revanche, si une contrainte de traction de 200 MPa est appliquée, l’orientation de la fissure correspondant à la valeur maximale de la force motrice est de 57°. On en déduit ainsi qu’une contrainte de traction peut accélérer la propagation des fissures qui tend à s’effectuer selon un angle élevé, tandis qu’une contrainte de compression peut retarder le développement des fissures et conduit à une propagation qui tend vers l’horizontale.
Importance du point de vue de l’ingénierie
Les recherches sur les mécanismes de fatigue ont permis d’identifier une des causes d’avarie prématurée des roulements [2]. Une avarie prématurée de roulement caractérisée par une fissuration de phase blanche (WEC) et une fissuration axiale a pu être reproduite avec succès lors d’essais en laboratoire pour lesquels la bague intérieure d’un roulement à rouleaux cylindriques était montée sur un arbre manchonné avec un défaut de circularité artificiel (ondulation). Il a été démontré au moyen d’une simulation par EF qu’un écart de forme de la portée du roulement, comme une ondulation, peut induire des contraintes de traction à proximité de la piste de la bague intérieure qui, au-delà d’une certaine limite, peuvent fragiliser le matériau et, combinées à une contrainte hertzienne, entraîner un déclenchement prématuré et un développement accéléré de fissures à partir des imperfections préexistantes du matériau.
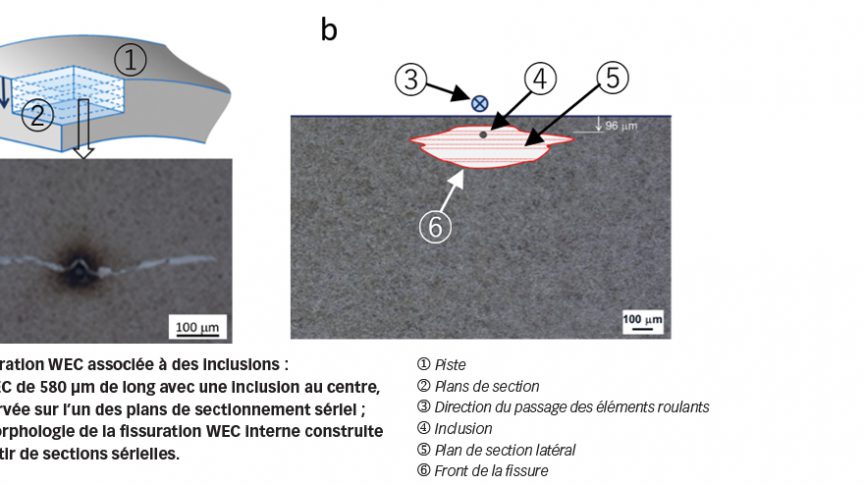
En outre, l’inspection métallographique à partir d’un sectionnement sériel à faibles intervalles des bagues testées a révélé que les fissures WEC, couramment observées sur des roulements victimes d’avaries prématurées, peuvent être déclenchées par des inclusions internes, comme illustré par la Fig. 8. Des recherches indépendantes évoquées dans le document [4] ont conduit à la même conclusion. Ce résultat est important car il apporte une clarification concernant l’origine de la fissuration WEC. Une fissure WEC est en substance une fissure interne comme une formation en ailes de papillon, qui peut être initiée à partir d’un concentrateur de contraintes, mais qui a atteint un stade avancé. Le frottement répété entre les surfaces de la fissure en FCR entraîne une altération microstructurelle progressive qui conduit à l’apparition de zones de phase blanche (WEA) à proximité de ces surfaces. Par conséquent, une WEC ou une WEA n’est pas la cause d’une avarie prématurée du roulement mais un symptôme de dommage par FCR avancé.
Résumé
La recherche sur les mécanismes de fatigue joue un rôle essentiel dans l’amélioration de la technologie des roulements pour relever les défis dans des applications exigeantes. Les travaux présentés ici montrent qu’une meilleure compréhension des imperfections des matériaux et de leurs effets sur les performances des roulements peut apporter un nouvel éclairage sur certains problèmes et permettre le développement de solutions pour réduire les taux d’avaries prématurées de roulements. Il est, par ailleurs, possible d’établir les limites de tolérance aux imperfections des matériaux.
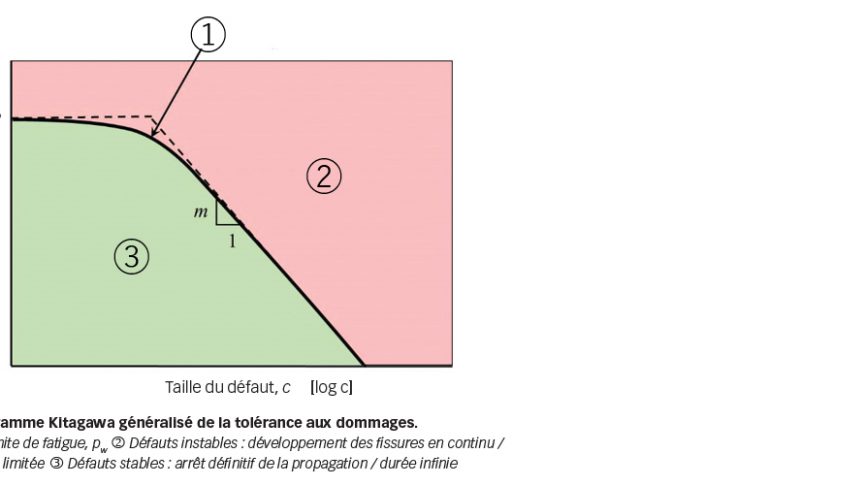
Les limites de tolérance aux imperfections du matériau peuvent être définies à partir d’un diagramme Kitagawa généralisé représentant, comme sur la Fig. 9, la limite de fatigue en termes de limite de pression de contact maximale, en fonction de la taille du défaut. Lorsque le défaut devient quasiment négligeable, la courbe est proche de la limite de fatigue intrinsèque du matériau de la matrice. En ce qui concerne les gros défauts, la limite de fatigue peut être déterminée à partir du seuil pour l’apparition d’une fissuration de fatigue, autrement dit de l’asymptote à pente constante en –m dont la valeur est fonction du type de défaut.
Le diagramme Kitagawa d’origine [6] a été proposé pour les défauts de type fissure avec m = 0,5. Le diagramme Kitagawa généralisé peut être appliqué à différents matériaux et différents types de défauts. Il a, par exemple, été utilisé pour établir la limite de tolérance pour les défauts d’insuffisance de matériau sur la surface des billes en nitrure de silicium de roulements hybrides [6]. Pour ce type de défaut, m est de 0,46.
Sur la base de la description du déclenchement et de la propagation de la fissuration de fatigue à partir d’inclusions internes, un modèle a été développé afin de prédire la résistance à la fatigue à très grand nombre de cycles (VHCF) et la limite de fatigue des aciers pour roulements [7]. Il a été démontré [8] que les limites de fatigue théoriques et les données d’essai VHCF coïncidaient avec la valeur de limite de fatigue indiquée dans la norme ISO 281:2007 relative au calcul de la durée de vie des roulements.
Références
[1] W. Solano-Alverez, H.K.D.H. Bhadeshia, White-etching matter in bearing steel. Part II: Distinguishing cause and effect in bearing steel failure, Metall. Mater. Trans. A 45A (2014) 4916-4931.
[2] J. Lai, K. Stadler, Investigation on the mechanisms of white etching crack (WEC) formation in rolling contact fatigue and identification of a root cause for bearing premature failure, Wear 364-365 (2016) 244-256.
[3] J.L. Johnson, Contact Mechanics, Cambridge University Press, 1985, Cambridge, UK.
[4] M. Evans, White structure flaking failure in bearings under rolling contact fatigue, PhD Thesis, University of Southampton, UK, 2013.
[5] H. Kitagawa, S. Takahashi, Applicability of fracture mechanics to small cracks or cracks in the early stage. In: Proceedings of the second international conference on mechanical behaviour of materials. ASM, 1976, pp. 627-631.
[6] J. Lai, Y. Kadin, C. Vieillard, Characterization and modelling of the degradation of silicon nitride balls with surface missing-material defects under lubricated rolling contact conditions, Wear 398-399 (2018) 146-157.
[7] J. Lai, T. Lund, K. Ryden, A. Gabelli, I. Strandell, The fatigue limit of bearing steels – Part I: A pragmatic approach to predict very high cycle fatigue strength, Int. J. Fatigue 38 (2012) 155-168.
[8] A. Gabelli, J. Lai, T. Lund, K. Rydén, I. Strandell, G.E. Morales-Espejel, The fatigue limit of bearing steels – Part II: Characterization for life rating standards, Int. J. Fatigue 38 (2012) 169-180.