
超越轴承思考齿轮
轴承和齿轮有很多共同点:它们都是通过润滑的接触面传递载荷的机械部件,并且经常协同工作。但是它们之间亦有着重要的区别:所需的疲劳循环次数大为不同,并且压力、速度和滑动也不尽相同。本文探讨了一种计算两者寿命的通用方法。
齿轮齿面的摩擦状况与滚动轴承的接触表面摩擦状况相似,但其程度不同。两类表面都有滚动/滑动(轴承的滑动摩擦比齿轮少得多),都具有很高的压力(轴承大于齿轮),并且两者的表面粗糙度与润滑膜厚度的数量级相同。所有这些都表明,应用于滚动轴承表面的相似表面寿命计算方法可以应用于齿轮接触表面。SKF表面损伤模型[1]是一个很好的例子,最初它是为滚动轴承开发的,后来应用于齿轮[2]。
目前,齿轮和滚动轴承的额定寿命是以不同的方法计算的。齿轮的选择和设计方法通常基于悬臂梁弯曲的路易斯方程[3]。美国齿轮制造协会(AGMA)标准[4]在路易斯方程中引入了额外的安全系数来表示齿根的应力集中、轮齿上的过载和载荷分布。除了考虑齿根的抗疲劳性外,AGMA还引入了对轮齿啮合表面产生的最大应力状态的验证。
AGMA引入了一个基于“干”接触应力的表面耐久性方程,因此,当接触应力超过某个临界值时,就可以认为轮齿会剥落。在过去的几十年中,这些方法已成功用于齿轮的设计和尺寸设定。但是,随着对缩小机械零件的尺寸以降低能耗和制造成本的工业化要求不断提高,工程师们一直在寻找更新的方式来优化机械零件的大小。
自动润滑、先进的表面光洁度和清洁度控制方面的最新摩擦学知识,可以显著提高齿轮的耐久性。这样可以为减少过度设计和提高机械效率提供新的机会。如今,在各个齿轮标准组织内部,已经做出非常大的努力来评估齿轮微剥落(微点蚀)风险[5],这表明了该课题在齿轮耐久性方面的重要性。然而,到目前为止,在齿轮设计过程中只能够间接考虑摩擦学方面的问题(所谓的微剥落风险),而且与滚动轴承业采取的做法相反,有关齿轮预期寿命的具体指南尚未出台。
相比之下,多年来一直利用独特的、专门的建模功能,将运行工况关联起来预测滚动接触的预期疲劳寿命。最重要的是:
- 采用Weibull材料强度最弱环节理论[6],考虑了材料的危险应力量值
- 使用Lundberg-Palmgren额定动载荷理论[7-8]
- 采用统计方法来定义疲劳寿命,即90%可靠性的L10寿命
- 运用Ioannides-Harris [9]疲劳应力准则,将润滑质量和清洁度的影响包含在滚动接触疲劳寿命中。
此外,最近引入了一种新的滚动接触疲劳寿命的通用方法,即所谓通用轴承寿命模型或GBLM [参见SKF《演进》2015第四期中的文章]。在这种新方法中,源自表面的损伤被明确地纳入到滚动接触的基本疲劳方程中。它考虑了作为失效风险的表面幸存概率,并排除了次表面的赫兹应力的影响[10-11]。这为使用专门的摩擦模型来描述滚动接触表面的相关失效提供了新的可能性。
齿轮尚未利用这些先进的建模概念。尽管由于Coy等人的开创性工作,在上世纪70年代人们做出了巨大的努力,但无论L10还是额定动载荷的使用都没有真正在齿轮设计中得到推广[12-15]。
本文的目的是简要讨论模型的一种变换[10],并研究其在齿轮上的潜在应用。主要概念在图1中进行了描述。对齿轮接触的表面和次表面的应力区域对齿轮啮合寿命的影响分别进行了分析,但它们都包含在L10估计中。
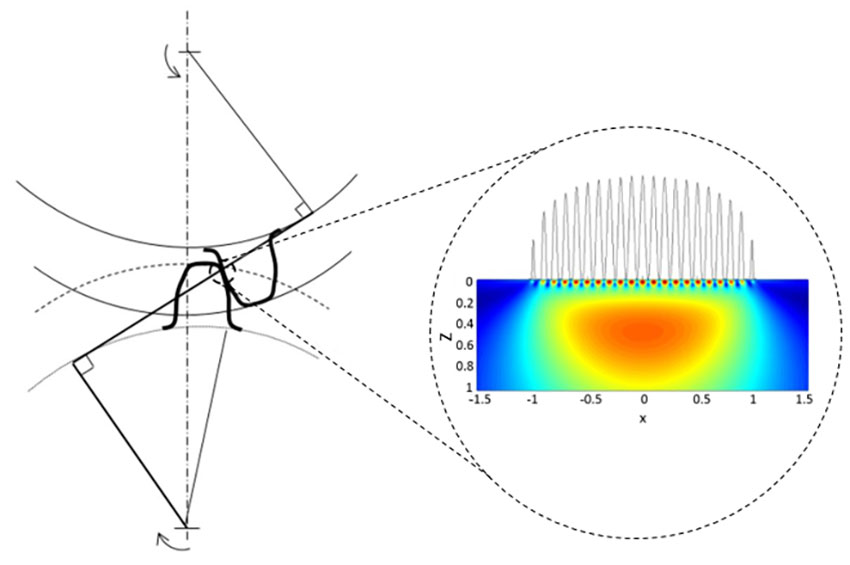
滚动轴承和齿轮的摩擦状况
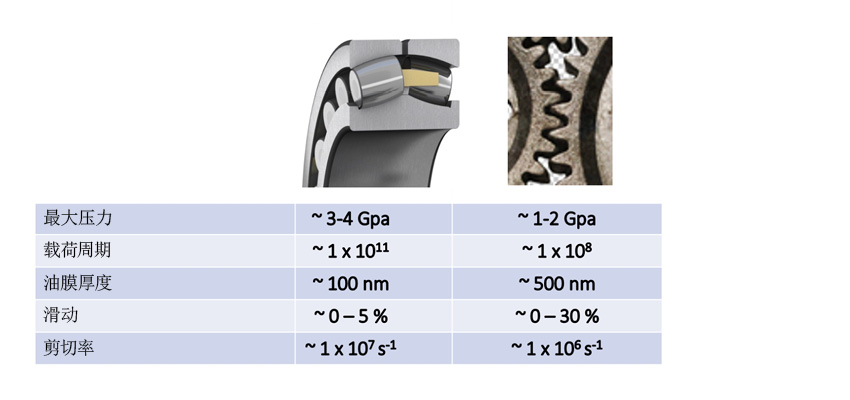
图2显示了齿轮和轴承典型摩擦状况之间的比较。可以看出,对滚动轴承运行状况的要求通常似乎要比对齿轮运行状况的要求更为苛刻,滚动轴承需承受更大的压力,拥有更长的使用寿命和更薄的润滑膜厚度。但是,齿轮呈现出更多的滑动并具有更高的粗糙度,这不利于表面的使用寿命。除此之外,齿轮通常具有与滚动/滑动方向相垂直的表面纹理,这与滚动轴承相反,一般情况下,滚动轴承的粗糙纹理是沿滚动方向的。在混合润滑条件下,这可能对轴承有利。
齿轮和滚动轴承中摩擦表面的寿命主要由两个重要因素决定:润滑质量和颗粒物污染,这两个方面在滚动轴承寿命的总体计算中(ISO 281)均已考虑,但在当前的齿轮寿命计算中并未被充分考虑。然而,最近提出的将表面幸存概率作为一种失效风险从次表面赫兹应力(GBLM)中分离出来的概念,或许有助于考虑齿轮中与滚动轴承相同的表面特性,并彻底统一齿轮和滚动轴承寿命的计算方法。
齿轮的表面损伤
如果润滑条件不足,齿轮如同轴承一样可能会遭遇表面损伤(也称为微剥落或发灰)。这可能发生在低润滑油粘度、齿面粗糙度过高以及潜含的低速条件下。换句话说,润滑状态不佳或Λ值偏低。
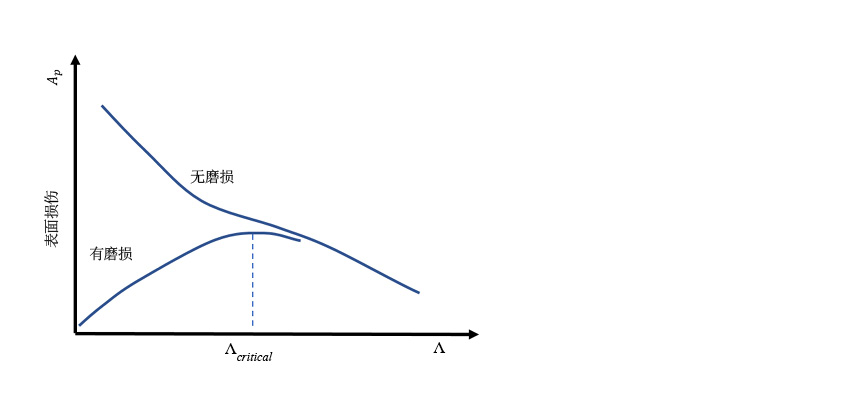
表面损伤是粗糙表面的疲劳与轻微磨损竞争的结果 [1-2]。充足的轻微磨损可能会去除凹凸不平的粗糙尖峰,并会降低局部压力,从而降低表面应力并减轻疲劳。轻微磨损也可能去除材料的疲劳层。轻微磨损太少可能会延长表面的磨合期,产生更大的损害并导致更多的表面损伤。在这种情况下,较低的Λ值可能会因为轻微磨损的增加而减轻表面损伤。否则表面损伤会增剧。如图3中所示。
在观察慢速表面时,齿轮表面损伤的另一个重要方面是所谓的负滑动状态。通常来说,较慢表面比较快表面更容易发生表面损伤。这种现象已经在文献[2]中得到了解释,该文献表明除了表面裂纹萌生和加速扩展的潜在影响外,较慢表面还会由于较快表面的粗糙度而产生更多的疲劳微循环次数的影响。
表面和次表面生存的齿轮寿命
拟建模型的详尽细节在文献[16]中给出;无论如何, 在此列出最终寿命方程还是很重要的
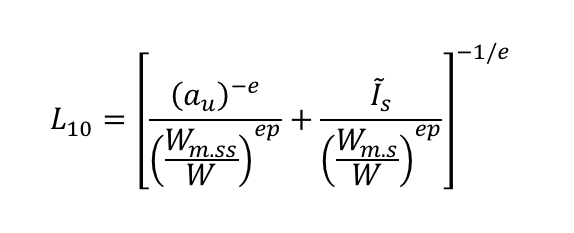
其中:
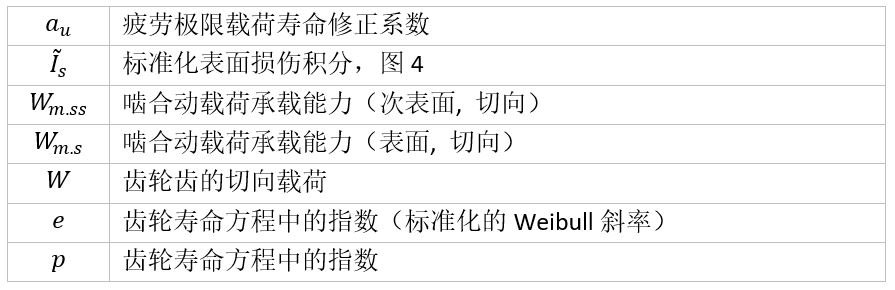
该寿命方程(1)有两个主要项,第一项(左侧)仅指可应用经典赫兹方程的次表面。第二项(右侧)仅指表面,使用更复杂的摩擦模型[1]来对其估计表面损伤。该方程遵循为滚动轴承开发的GBLM相同的概念。
过去Coy等人的工作已经给出了用于齿轮动载荷承载能力(次表面)Wm.ss的方程。[12-15]。在文献[16]中引入了动载荷承载能力(表面)Wm.s的方程。请注意,与轴承不同,此处还引入了表面的动载荷承载能力,相当于在轴承中为表面也引入了一个“C”值。
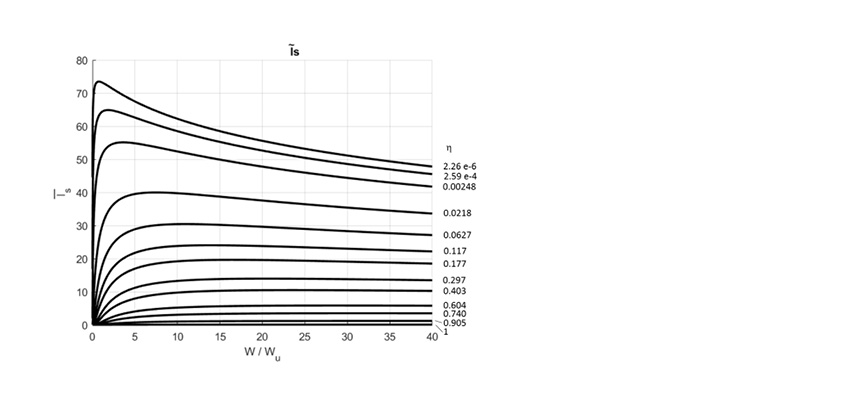
应用案例
文献[17]比较了两个直齿轮组的寿命,一个齿轮组只有磨削表面,另一个具有超精加工表面。参考文献中给出了所有齿轮数据、材料、几何形状和工作条件。在相同的工作条件下测试这两个齿轮组,不同的是,磨削表面齿轮组由于粗糙度较高(Λ≈1.13),在较低Λ值的情况下性能变差,而超精加工表面齿轮组由于粗糙度较低(Λ≈6.17),则具有较好的润滑质量。文献[17]中给出的磨削表面齿轮和超精加工表面齿轮的测试数据已经数字化并重新绘制在图5中,图中给出了测量数据和计算数据的比较图形。
图5显示了置信区间有一点重叠,可能需要更多的失效试验(尤其是对于超精加工的群组)以减少不确定性。无论哪一种情况,从数据中都可以观察到寿命的明显区别。该图还显示了应用方程(1)(星号)计算出的寿命。
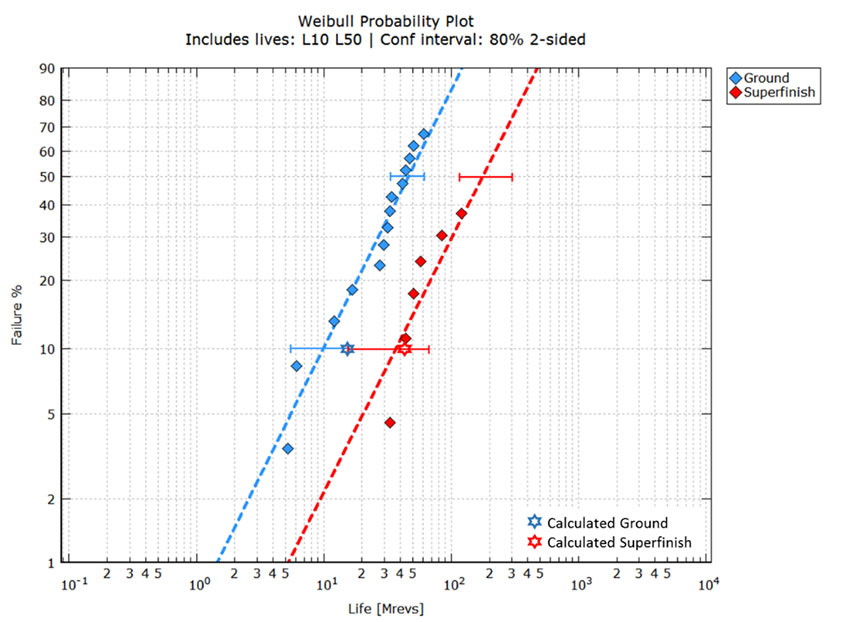
最初为滚动轴承开发、考虑到表面和次表面寿命的滚动接触疲劳概念模型现已应用于齿轮。作为一个应用实例,它说明了润滑质量的影响。
一旦在不同的应用条件下对齿轮进行更多的试验结果校正,尤其是考虑材料、润滑、表面光洁度和颗粒物污染的影响,这一概念模型便可以演变为一个预测模型。
但是,即使是在概念阶段,该模型也已经可以为参考文献[12-15、17]中的直齿轮测试提供正确的数值,这是齿轮寿命模型首次给出表面的一个估算参数(表面动载荷承载能力)。
根据此处提供的分析,可以得出以下结论:
- 当前的方法将表面和次表面的寿命相分离。由于分析了多个区域,因此通过增加齿轮寿命建模的灵活性可以获得显著收获。除了赫兹滚动接触疲劳之外,还使得工程师能够引用表面失效模型。
- 由于表面效应直接包含在公式中,因此借助这一方法,可以利用从高级摩擦模型的应用中获得的知识。未来可能会包含诸如齿根应力的非摩擦效应。
- 除了齿轮的次表面动载荷承载能力外,还引入表面动载荷承载能力,这是一项创新,它将赋予估算特殊功能齿轮灵活性,诸如表面处理、涂层和表面精加工等明显影响表面性能的特殊性。
- 特别是在齿轮箱的设计中,齿轮和滚动轴承寿命计算方法的统一将非常有用,这不仅是考虑到轴承和齿轮的相同假设,还鉴于两者的共同可靠性。





