Les engrenages sont des éléments mécaniques de contact qui sont confrontés à des difficultés, à maints égards, similaires à celles des roulements. Ils présentent également des différences notables. Dans bon nombre d’applications, roulements et engrenages fonctionnent de concert et en étroite interaction. Les ingénieurs qui travaillent avec des roulements ont souvent besoin d’en savoir un minimum sur les conditions de fonctionnement des engrenages car celles-ci peuvent influer sur le comportement des roulements. Pourtant, malgré des similitudes sur le plan tribologique, les méthodes de calcul de durée de vie sont très différentes entre les deux types de pièces. Cet article applique aux engrenages des notions de durée des surfaces bien connues dans le domaine des roulements et étudie la possibilité d’étendre à ce type de pièce la nouvelle méthode de calcul de la durée de vie des roulements qui intègre une distinction entre surface et sous-couche. La méthodologie appliquée aux roulements et aux engrenages serait ainsi, pour la première fois, exactement la même.

Les conditions tribologiques des surfaces des flancs de dentures sont similaires à celles des surfaces de contact des roulements, mais l’amplitude diffère. Ces deux types de surfaces se caractérisent par un roulement/glissement (moins de glissement dans les roulements par rapport aux engrenages), des pressions élevées (plus élevées pour les roulements que pour les engrenages) et un état de surface du même ordre de grandeur que l’épaisseur de film lubrifiant. Tous ces points plaident en faveur de la possibilité d’appliquer des méthodes de calcul de la durée des surfaces de roulements aux surfaces de contact dans les engrenages. Le modèle SKF d’altération de la surface [1], développé initialement pour les roulements et appliqué par la suite aux engrenages [2], en est un bon exemple.

Aujourd’hui, les durées de vie nominales des engrenages et des roulements sont calculées de manières différentes. Les méthodes de sélection et de conception des engrenages sont généralement basées sur la formule de Lewis [3] pour la flexion des poutres. La norme AGMA [4] introduit des coefficients de sécurité supplémentaires dans l’équation de Lewis afin de tenir compte de la concentration de contraintes en pied de dent et de la distribution de la charge sur la dent. En plus de la résistance à la fatigue du pied de dent, cette norme intègre également la vérification de l’état de contrainte maximale sur la surface de contact de la dent.

Elle introduit une équation de durée de la surface basée sur des contraintes de contact « sec », de sorte que, lorsque la contrainte de contact dépasse une certaine valeur critique, on considère que les dents de l’engrenage présentent un écaillage. Ces méthodes sont utilisées avec succès pour la conception et le dimensionnement des engrenages depuis plusieurs décennies. Cependant, face à une demande croissante de l’industrie pour réduire les dimensions des pièces mécaniques, la consommation d’énergie et les coûts de production, les ingénieurs sont constamment en quête de solutions innovantes pour optimiser les dimensions des pièces.

Les dernières connaissances en tribologie appliquées à la lubrification automatique, un fini de surface amélioré et le contrôle de la propreté peuvent clairement contribuer à optimiser la durée de vie de l’engrenage. Il en résulte de nouvelles opportunités de réduction du surdimensionnement et d’amélioration de l’efficacité mécanique. Aujourd’hui, au sein des organismes de normalisation des engrenages, des efforts considérables sont déployés pour évaluer le risque de micro-écaillage (micropiqûres) des engrenages [5], ce qui montre l’importance de cet aspect pour la durée de vie de ces pièces. Cependant, à ce jour, les aspects tribologiques (autrement dit le risque de micro-écaillage) ne peuvent être pris en compte dans le processus de conception des engrenages que de manière indirecte et, contrairement aux roulements, aucune ligne directrice n’est fournie concernant la durée de vie nominale des engrenages.

À l’inverse, les roulements tirent profit depuis de nombreuses années de fonctionnalités de modélisation uniques et pointues pour la prédiction de la durée en fatigue théorique du contact de roulement, en fonction des conditions de service. Voici un aperçu des plus significatives d’entre elles :

• l’application de la théorie de Weibull du maillon le plus faible pour la résistance des matériaux [6], qui tient compte du volume de contrainte du matériau à risque ;
• la mise en pratique de la théorie de la charge dynamique de Lundberg-Palmgren [7-8] ;
• l’approche statistique dans la définition de la limite d’endurance en fatigue, à savoir une fiabilité de 90 % pour la durée de vie L₁₀ ;
• l’application du critère de contrainte de fatigue de Ioannides-Harris [9] pour tenir compte de l’effet de la qualité de la lubrification et de la propreté dans le calcul de la durée en fatigue du contact de roulement.

De plus, une nouvelle approche générale pour le calcul de la durée en fatigue du contact de roulement a été introduite très récemment. Il s’agit du Modèle généralisé de durée de vie des roulements ou GBLM (Generalized Bearing Life Mode) [Article SKF Evolution n° 4-2015]. Avec cette nouvelle méthode, les dommages initiés en surface sont représentés explicitement dans les équations de base de fatigue des contacts de roulement. La probabilité de survie de la surface est considérée comme un risque de défaillance distinct des contraintes hertziennes en sous-couche [10-11]. Cette méthode ouvre de nouvelles perspectives pour l’utilisation de modèles tribologiques spécialisés pour décrire des défaillances du contact de roulement liées à la surface.

Les engrenages ne bénéficient pas encore de ces concepts de modélisation. L’utilisation de la durée L₁₀ ou de la charge dynamique dans la conception des engrenages ne s’est pas non plus développée, malgré des efforts significatifs déployés dans les années 70, dans le cadre des travaux de recherche de Coy et al. [12-15].

Notre propos porte ici sur les possibilités d’adaptation du modèle [10] en vue de son application aux engrenages. Le concept principal est représenté sur la Fig. 1. Les zones de contraintes sur la surface et en sous-couche du contact d’engrenage sont analysées séparément pour déterminer leur contribution à la survie de l’engrènement, mais incluses ensemble dans l’estimation de la durée L₁₀.

Cela sera utile pour illustrer les possibilités offertes par une approche plus intégrée pour le calcul de la durée de vie des surfaces de contact dans les engrenages et les avantages de la méthode proposée par rapport aux méthodes actuelles.

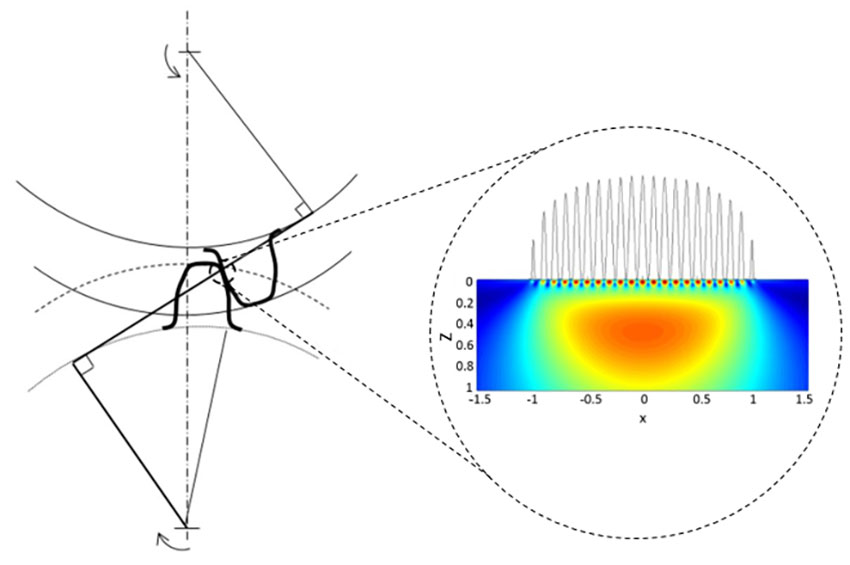
Conditions tribologiques des roulements et engrenages

La Fig. 2 établit une comparaison entre les conditions tribologiques typiques des engrenages et celles des roulements. On constate que, de manière générale, les conditions dans les roulements sont plus difficiles que dans les engrenages : pressions supérieures, durées de vie requises plus longues et film lubrifiant moins épais. Cependant, les engrenages présentent un glissement supérieur et une plus grande rugosité de surface, des conditions peu favorables à une longue durée de vie des surfaces. En outre, ils se caractérisent par une orientation transversale de la rugosité de surface par rapport au sens du roulement/glissement, contrairement aux roulements dans lesquels la rugosité est généralement orientée dans le sens du roulement. Dans des conditions de lubrification mixte, les roulements sont avantagés.

La durée de vie d’une surface tribologique dans des engrenages ou des roulements est principalement déterminée par deux facteurs importants : la qualité de la lubrification et la contamination solide, deux aspects qui sont pris en compte dans le calcul global de la durée de vie des roulements (ISO 281), mais de façon incomplète dans le calcul actuel de la durée de vie des engrenages. Cependant, le concept récent d’introduction de la probabilité de survie des surfaces comme risque de défaillance distinct des contraintes hertziennes en sous-couche (modèle GBLM) peut aider à considérer les mêmes aspects de la surface dans les engrenages et dans les roulements et à unifier, une fois pour toutes, les méthodes de calcul.

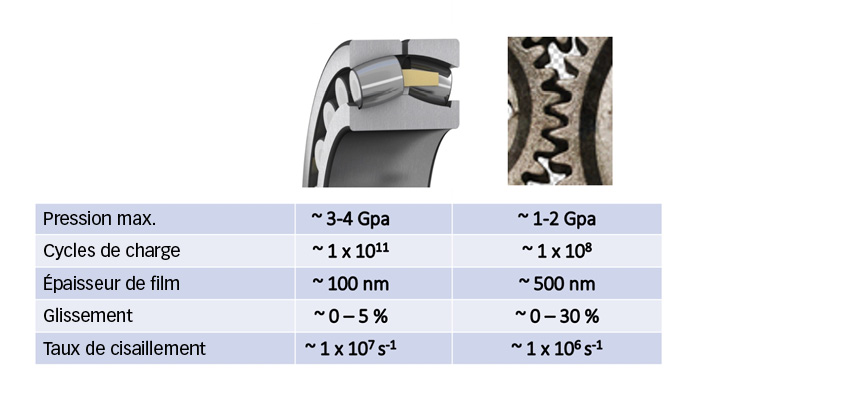
Altération de la surface dans les engrenages

Les engrenages, comme les roulements, peuvent être sujets à une altération de la surface (également appelée microécaillage ou décoloration grise) si les conditions de lubrification ne sont pas satisfaisantes. Ce phénomène peut se produire en cas de faible viscosité du lubrifiant, de rugosité excessive dans les engrenages, ainsi qu’à basse vitesse ; autrement dit, lorsque la qualité de la lubrification est médiocre ou en présence d’un faible ratio Λ.

L’altération de la surface résulte de la fatigue en surface au niveau d’aspérités combinée à une usure douce [1-2]. Une usure douce suffisante est susceptible de gommer les sommets des aspérités et peut réduire les pressions locales et, donc, les contraintes en surface et la fatigue. L’usure douce peut aussi enlever les couches de matériau sujettes à la fatigue. Une usure trop douce est susceptible de prolonger la phase de rodage des surfaces, ce qui majore les dommages et l’altération de la surface. Dans cette condition, des valeurs Λ inférieures peuvent se traduire par une altération de la surface inférieure car l’usure augmente ; dans les autres cas, l’altération de la surface augmente. C’est ce qu’illustre la Fig. 3.

Un autre aspect important de l’altération de la surface dans les engrenages est le glissement dit négatif, lorsque l’on observe la surface la plus lente. On dit souvent que la surface la plus lente est plus sujette à l’altération que la surface la plus rapide. Ce phénomène est expliqué dans la référence [2] qui montre que, sur une surface plus lente, la rugosité de la surface la plus rapide produit des micro-cycles de fatigue plus nombreux, en plus des autres effets potentiels que sont l’ouverture d’une fissure en surface et une propagation plus rapide.

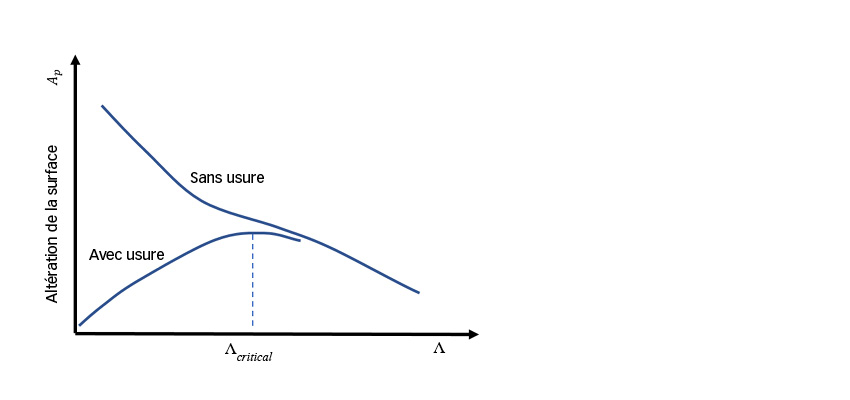
Durée de vie de l’engrenage avec survie de la surface et de la sous-couche

Tous les détails du modèle proposé sont fournis par la référence [16]. Il nous semble toutefois important de reprendre ici la formule finale de durée de vie

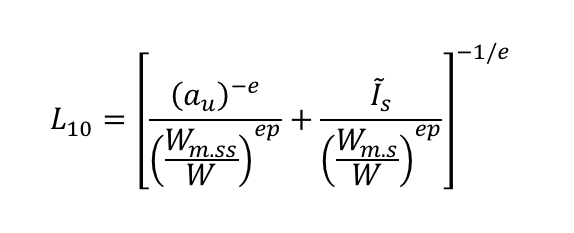
où :

Cette formule de durée (1) comprend deux termes principaux, le premier (à gauche) porte uniquement sur la sous-couche à laquelle des équations hertziennes classiques peuvent être appliquées. Le second terme (à droite) porte uniquement sur la surface pour laquelle des modèles tribologiques plus complexes [1] sont utilisés pour estimer son altération. Cette équation repose sur le même principe que le modèle GBLM développé pour les roulements.

Des équations pour le calcul de la capacité de charge dynamique des engrenages (en sous-couche) W_m.ss ont été fournies par le passé suite aux travaux de Coy et al. [12-15]. Une équation pour la capacité de charge dynamique (de la surface) W_m.s est introduite dans la référence [16]. Notons que, contrairement aux roulements, la capacité de charge dynamique de la surface est également introduite. Dans le cas des roulements, cela reviendrait à introduire une valeur « C » également pour la surface.

Fig. 4. Exemple de valeur Ĩ_s normalisée utilisée, avec η représentant le facteur environnemental η=η_b η_c (comme pour les roulements).

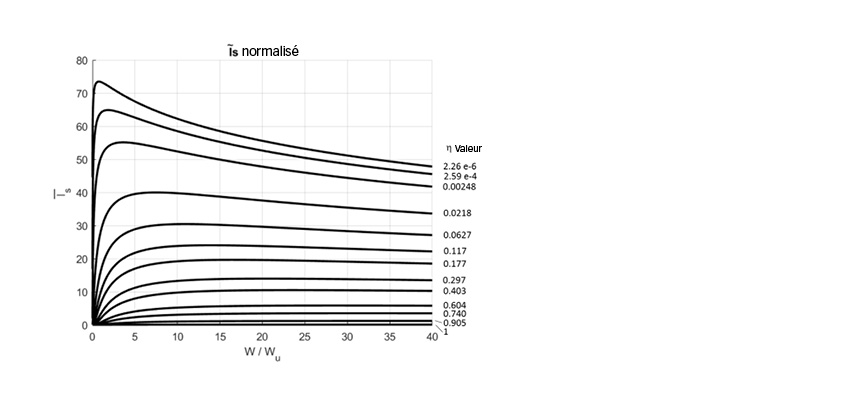
Exemple d’application

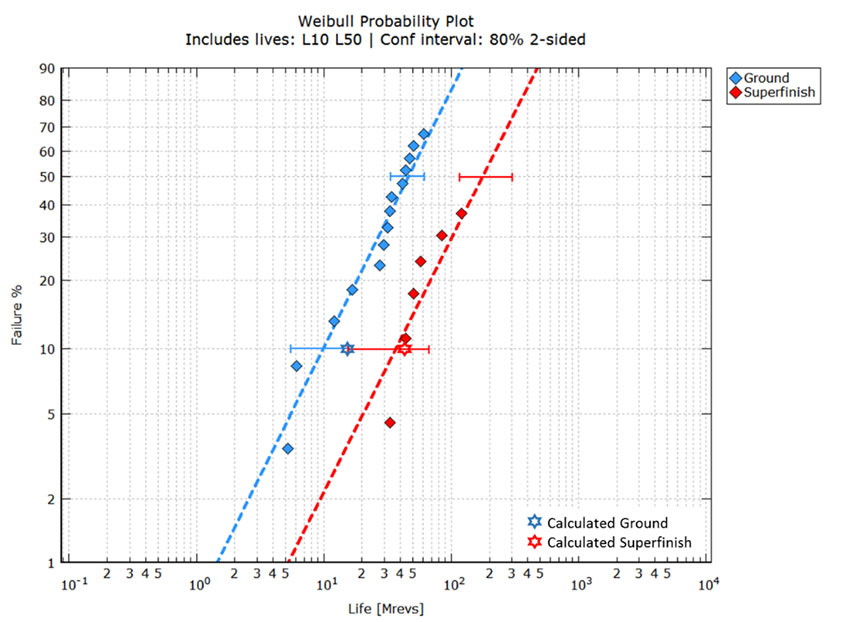
La référence [17] compare les durées de vie de deux groupes de roues à denture droite, l’un avec des surfaces rectifiées et l’autre, avec des surfaces superfinies. Toutes les données relatives aux engrenages, les matériaux, la géométrie et les conditions de service sont indiquées dans le document de référence. Les deux groupes sont testés dans les mêmes conditions de service, à la différence près que le groupe avec surfaces rectifiées présente une dégradation sous un ratio Λ inférieur, du fait de sa rugosité supérieure (Λ≈1,13), tandis que le groupe avec des surfaces superfinies présente une qualité de lubrification supérieure du fait de sa rugosité inférieure (Λ≈6,17). Les résultats d’essai présentés dans le document de référence [17] pour les engrenages rectifiés et superfinis ont été numérisés et repris sous forme graphique à la Fig. 5 où ils sont comparés aux données théoriques.

La Fig. 5 montre que les intervalles de confiance se chevauchent légèrement ; des défaillances supplémentaires seraient nécessaires (en particulier pour la variante superfinie) pour réduire l’incertitude. Dans chaque cas, les données montrent une nette différenciation des durées de vie. Cette figure présente également les durées de vie calculées en appliquant l’équation (1) (étoiles).

Les durées de vie théoriques sont en légère surestimation par rapport aux mesures, surtout pour la variante rectifiée. Des essais supplémentaires permettraient d’affiner le modèle selon les méthodes déjà utilisées pour les roulements. Toutefois, à ce stade, l’objectif principal est de fournir une première évaluation de la théorie de base sans l’interférence des facteurs d’étalonnage. Si l’on tient compte de cet aspect, d’après la Fig. 5, la comparaison entre les données d’essai et les résultats théoriques issus de la méthodologie présentée ici montre une très bonne corrélation.

Conclusions

Un modèle conceptuel, avec survies de la surface et de la sous-couche pour la fatigue de contact de roulement, développé initialement pour les roulements, a été adapté aux engrenages. L’effet de la qualité de la lubrification a été démontré dans le cadre d’un exemple d’application.

Le modèle conceptuel peut évoluer vers un modèle prédictif une fois affiné avec des résultats plus expérimentaux obtenus sur des engrenages dans différentes conditions d’application, pour tenir compte en particulier de l’impact du matériau, de la lubrification, de la finition de surface et de la contamination par des particules.

Toutefois, même au stade du concept, le modèle peut déjà fournir les valeurs correctes pour des essais avec des roues à denture droite, d’après les références [12-15, 17]. Pour la première fois, un modèle de durée de vie des engrenages intègre un paramètre d’évaluation pour la surface (capacité de charge dynamique de la surface).

Les conclusions de l’analyse présentée ici sont les suivantes :

1. L’approche actuelle introduit une séparation entre survie de la surface et survie de la sous-couche. Elle peut ainsi offrir des avantages significatifs du fait d’une flexibilité accrue dans la modélisation de la durée de vie des engrenages puisque plusieurs régions sont analysées. Cela permet aux ingénieurs d’introduire des modes de défaillance en surface en plus de la fatigue de contact de roulement hertzien.
2. Comme les effets en surface sont directement intégrés à la formule, cette approche permet d’exploiter des connaissances issues de l’utilisation de modèles tribologiques avancés. Des effets non-tribologiques pourraient être inclus à l’avenir, comme les contraintes en pied de dent.
3. L’introduction d’une capacité de charge dynamique de la surface en plus de la capacité de charge dynamique de la sous-couche dans les engrenages est une innovation qui devrait apporter de la souplesse pour l’évaluation d’engrenages présentant des particularités qui influent clairement sur les performances de la surface : traitements, revêtements et finitions de surface.
4. Dans le domaine de la conception des boîtes de vitesses notamment, une homologation des méthodes de calcul de durée entre engrenages et roulements serait extrêmement utile, pour la prise en compte non seulement d’hypothèses identiques pour les roulements et les engrenages, mais aussi des fiabilités communes.