Tiny deviations in the roundness of bearing elements can have an impact on bearing quality.Periodic form deviations in the range of an angstrom (10^-10 m) may influence bearing quality. Divergences from the ideal round form of bearing components coupled with general bearing parameters are very important. This is especially relevant when the form deviations are periodically distributed around the circumference of a ring – or a rolling element raceway. Then the assembled bearing has the potential of activating a structural resonance in the customer’s application.
The inherent resonance of some systems, coupled with periodic deviations in the bearing elements, can create a dramatic amplification in the resonance that could cause operational problems. Such a situation could typically occur when the resonance has a high Q-factor with low damping. The response in the application may be a factor of thousands higher than the corresponding low-activation amplitude.
The periodic form deviations of high-precision bearings, called waves, are already at higher order numbers – with amplitudes in the nanometre (10^-9 m) and even picometre (10^-12 m) range – which can produce noise in operating circumstances.

Modes of vibration
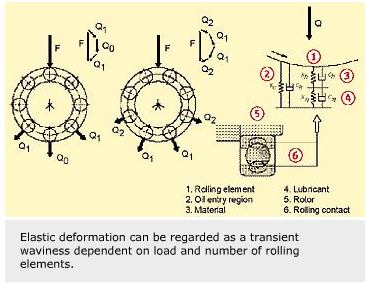
In general, such waves may introduce three different modes of vibration. The least significant mode is called extensional vibration and occurs on waves with multiple lobes or when the number of lobes of a particular wave, for example, on an inner ring, is equal to the number of rolling elements. Here, the outer ring will be extended in all directions when the rolling elements are all together on the top of the wave. The outer ring and the bearing housing strongly resist this mode of vibration, so it is not dangerous from the point of view of vibrations. Torque could represent more of a threat, but this is not considered in this article.
The second vibrational mode, the flexural mode, is created when there is a difference of two between the number of lobes and the number of rolling elements. Then an oval will be formed. This ellipse circles around and introduces a vibration that experiences less damping by the outer ring and the bearing housing than in the case of extensional vibration. This flexural mode is more problematic than the extensional mode and can also occur on all multiples of lobes.
By far the most dangerous case is the rigid-body mode. It occurs when there is a difference of one between the number of lobes and the number of rolling elements.
In those moments when the topmost rolling element is on top of the wave, two rolling elements on the bottom are close to the valleys of the wave. The centre of the shaft becomes slightly below the ideal axis. In the next moment, the situation is reversed, and the shaft axis is slightly above the ideal axis. In this case, there is no damping provided by the outer ring and, therefore, no damping support to improve the situation. If at certain rotational speeds structural resonances are met, then a significant response may occur in the application.
These problems can also occur on all multiples of the dangerous number of lobes.

The resonance phenomena
In general, resonance can be seen as an exchange of energy between two different types of storage media at a specific exchange speed. In mechanics, a mass and a spring representation are needed. When these two components are combined and activated, the kinetic energy of the mass is put into the tension or compression of the spring until the moving mass is pumped out and stands still. The charged spring now will accelerate the mass in the opposite direction, putting back the energy from tension into the kinetic energy of the mass. When the mass has reached its highest speed at the neutral position of the spring, the still-moving mass expands the spring during braking, thus giving back the energy to the spring.
The exchange-speed course follows a sinusoidal wave form of a particular period. The reciprocal of the periodic time defines the resonance characteristics of the system as a whole and is, therefore, called the eigenfrequency – the natural or resonance frequency. At this characteristic frequency, only a very small amount of external energy is needed to keep the system running.
This fact can be illustrated by a simple example. A father pushing his child on a swing will adjust his pushes to the resonance frequency of the pendulum and will be able to keep his child swinging with little effort.
In other words, an activation source can push a system to extreme responses (resonances) even with a very small activation energy. The only preconditions are that the target system has specific resonances and the activation source meets one of these frequencies in phase. In the swing example, the resonance is desirable. In all application cases where bearings, even with very small periodic waves, may be activators, these situations have to be avoided absolutely.
An activation source outside the eigenfrequencies of a system has very little chance or needs very high energy to make a target system respond. Applying this to the example of the swing, the father would smash his nose when trying to push the swing out of phase with a different activation frequency.
If there were no damping in a vibrating system, an oscillation once activated would never stop. Damping means that energy is taken out of the system by converting it into other forms, such as via friction into heat. Now the question must be answered: Which parameters influence the frequency of a resonance and its possible amplitude of excursion? Firstly, the mass gives an influence by its inertia. The higher the mass, the more force is needed to accelerate it. Thus a higher mass will bring resonances down to lower frequencies. Secondly, the spring effect must be considered. Technically this is described by defining the spring rate: the higher the spring rate, the higher the force a spring is able to apply to a connected mass. Due to the higher possible acceleration of the mass, the resonance is shifted to higher frequencies.
Thirdly, there is an influence that is applied by factors that have a possibility to damp the system. In most cases, this is friction.
The example of a classical mass-spring system should help to put the influencing parameters into the frame of a formula. Damping is assumed to be zero, and the mass should be pushed out of the neutral position by an activating force, F_A. This activation force must be in balance with the push-back force, F_S, applied by the spring:

According to Newton’s Second Law of Motion, the activation force equals mass, m, times acceleration, a. For a linear spring, the spring force is the spring rate, c, times the excursion, s:

With acceleration being the second derivative of the excursion, s, a linear homogeneous second-order differential equation describes the system:

The field of solutions to this equation as a function of time, t, is:

The Pythagorean sum of C₁ and C₂ represent the amplitude of the excursion. The argument of the sinusoidal functions includes the frequency, f_r, of the resonant sinusoidal vibration. According to the derivation, vibration depends on the mass and the spring rate as follows:

When the activation source is switched off, in a damped system the oscillation would approach zero asymptotically while following a descending e-function. But damping has no influence on the frequency of resonance.

Bearing as exciter
Perfectly round raceways are impossible to achieve in practice. So, when overrolled, the raceway will cause a certain excitation of vibrations. This is mathematically related to the magnitude of the waviness, to the number of waves and to the overrolling speed.
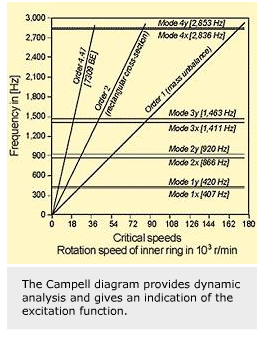
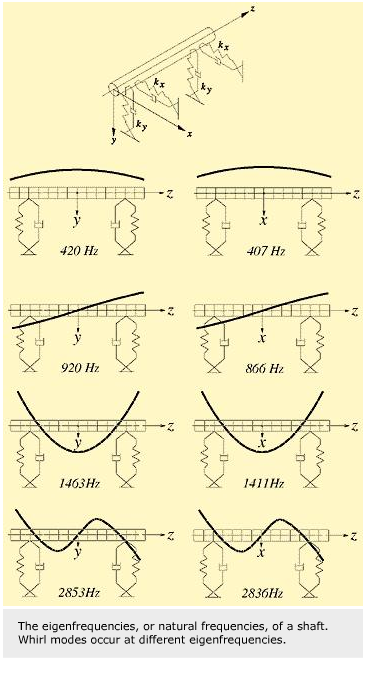
The mass and the stiffness of coupled parts and their eigenfrequencies play an important role. A rotor dynamic analysis considers the excitation function in a Campell diagram.
The eigenfrequencies and associated mode shapes for a flexible shaft including the effect of non-isotropic bearing stiffness coefficients are considered. In such a system, all the whirl modes occur at different eigenfrequencies.
The corresponding natural whirl frequencies are given in the Campell diagram by the horizontal lines, marked by the mode number. The inclined lines, the order lines, marked “order No. 1,” etc., represent the excitation factors, e.g., mass unbalance No. 1. The speed at which these lines intersect is a critical speed. SKF calculates the critical speed maps with the help of a computer program.
A similar effect to waviness comes from the elastic deformation of the raceways caused by the contact forces between rolling elements and raceways. The elastic deformation is seen as a transient waviness, depending on the load and the number of rolling elements or on the stiffness of the bearing.
The interaction between rotor dynamics and the bearing quality shows that a good bearing is advantageous but is no guarantee for success in the application. Equally, success in the application is no evidence of high bearing quality. It may be simply a lucky pairing of rotor properties and bearing imperfections.

A case study
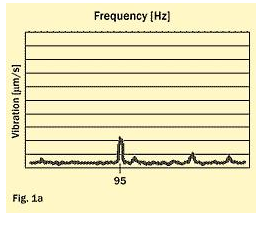
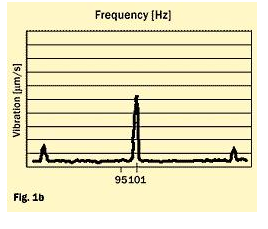
By applying a template, it is possible during production to select bearings that give less excitation at the critical resonances. Figure 1 represents a practical example with two bearings installed in a machine.
Bearing 1 (fig. 1a) has a rather low vibration response from its waviness characteristics but a relatively high amplitude at around 95 Hz, when measured with a vibration tester operated at 700 r/min (11.66 Hz).
Bearing 2 (fig. 1b) shows an amplitude 2.5 times higher, but this occurs at 101 Hz. One would assume that bearing 1 operates more quietly than bearing 2. In practice, the machine where the bearings were installed runs at 3600 r/min. (60 Hz).
Bearing 2 operated well, while bearing 1 showed a disturbing vibration peak coinciding with an eigenfrequency of the shaft at 488.5 Hz (because 95/11.66 = 488.5/60 = order No. 8.14.). The reason for that is waviness with very little amplitude.
To avoid resonances at the critical speed, applying the template would limit the vibration/excitation at this frequency. In turn, the waviness that causes vibrations at 95 Hz must be limited. It is better to set the limit in a range, e.g. of 91 Hz to 97 Hz, and to consider speed variations, geometrical tolerances and loading differences (fig. 1c).
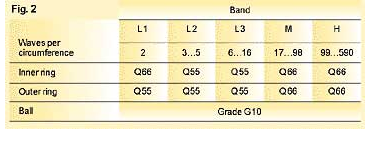
By experience, applying the template results in a waviness specification as shown in fig. 2.
In the case where the machine would run at 3,000 r/min. (50 Hz), the order number would be No. 9.77 = 488.5/50. It would be equivalent to an excitation at 407 Hz, which corresponds to a non-resonant condition. Bearing 1 would work well because 407 Hz is below the eigenfrequency of 488.5 Hz).
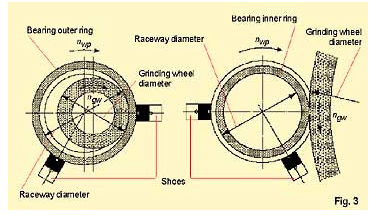
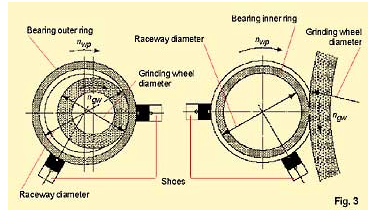
Figure 3 demonstrates that the relative speed of the grinding wheel and the workpiece (bearing ring), as well as the raceway diameter and the cutting force, are of importance. A pre-deformation of the bearing ring and the stiffness of the supports – grinding spindle as well as the shoes and drivers – influence the cutting force and its fluctuation or the vibration while machining. This results in deviations of the ideal round form, which means waviness.

Waviness might be caused by the following processes:

• Heat treatment can result in ovality, order No. 2 or two waves per circumference.
• Centreless grinding or turning with a clamping jig at three points typically causes a Reuleaux triangle, order No. 3 or three waves per circumference.
• Turning with clamping at four points causes a square, order No. 4 or four waves per circumference
• A higher order of waviness comes usually from the relation (superposition) of grinding wheel and bearing ring speed as well as from disturbing resonances of the machines.

Any subsequent honing processes mainly influence the magnitude of waviness. Higher waviness orders are reduced considerably, although low orders will remain or can be even magnified by such treatment.

Conclusions
Standard production allows waviness values from 28 mm/s for the high-band of bearing 7309 BE, for example. In precision bearing production, which includes optimised operating speeds and preventive quality related maintenance, the waviness values for the same bearing size are re- duced by a factor of between 1.5 and 3.
Considering an even harmonic distribution within the filter band and a rotational speed of 183 r/min., a wave with 200 lobes per circumference for instance, is just allowed to have a displacement proportional amplitude of 0.46 nm, which seems to be negligible.
It is almost unbelievable, but real cases show that waviness in the range of nanometres can cause high vibrations when exciting at, or close to, eigenfrequencies.

Hubert Köttritsch and
Franz Reithuber,
SKF Österreich AG, Steyr, Austria